重回帰分析とは？概要から分析の流れまでわかりやすく解説

ビジネスで重要な「来月の売上はいくらになりそうか？」や「売上に貢献する要素は何か？」といった問いに対して、明確な根拠を持って答えることができないという課題を抱えている方は多いと思います。本稿を読んで重回帰分析を理解・実施できるようになると、これらの問いに対して統計的な回答を得ることができます。

本稿は、数学に自信がないという方にもイメージを掴んでもらいやすくするために、一貫してとあるカフェチェーンの例を用いて解説します。カフェチェーンの売上に対して重回帰分析を行うと、売上予測や以下のような推定ができます。

是非、最後まで読み進めて重回帰分析をマスターしましょう！

1.重回帰分析の概要

重回帰分析が何かを理解するためには、最初に「回帰分析」について理解する必要があります。

1-1.回帰分析とは複数データの関連性を明らかにする手法である

回帰分析とは、複数データの関連性を明らかにする統計手法の一つです。ある成果の値変動に別の要素がどのくらい影響を与えているかを分析することができます。

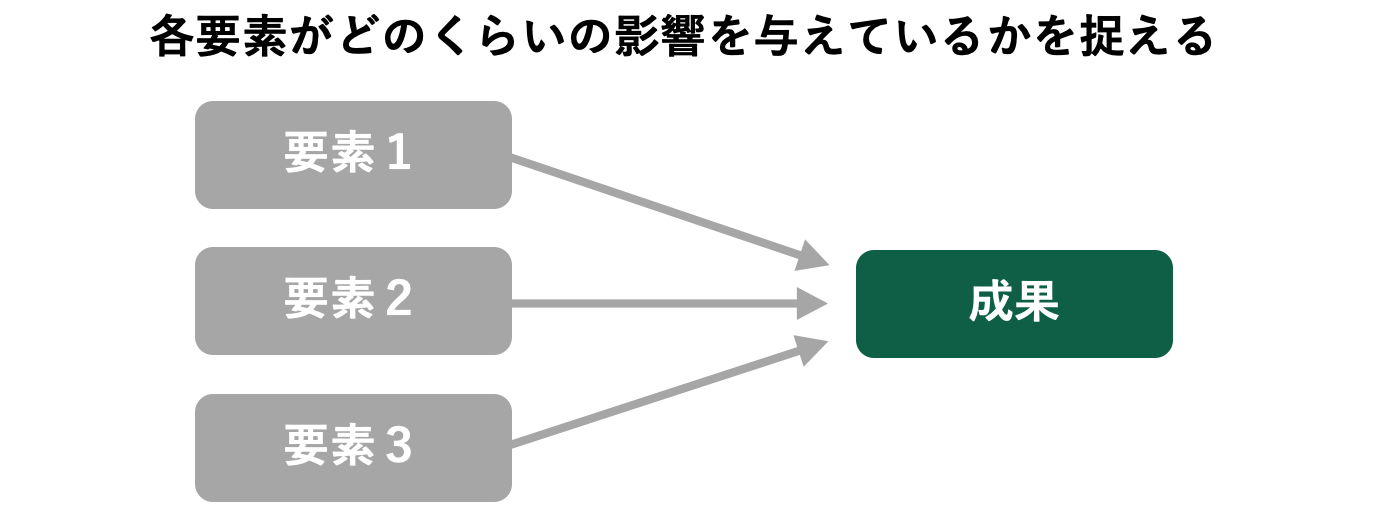
回帰分析について理解するにあたり、必ず知っておきたいものとして”目的変数”と”説明変数”の2つがあります。分析対象の成果を目的変数と呼び、それに影響を与えているであろう要素を説明変数と呼びます。よって上の図は以下のように示すことができます。

目的変数のことを従属変数、説明変数のことを独立変数と呼ぶこともあります。どちらも分析における専門用語ですが、広く使用されていてかつ理解しやすい（してもらいやすい）目的変数と説明変数を覚えておくことをおすすめします。

回帰分析では、説明変数が目的変数に与える影響の程度を数値化し、それらの関係を直線などの式で表します。

言葉だけで理解するのは難しいので、あるカフェチェーンのデータを例にみていきましょう。下記のようにカフェチェーン10店舗それぞれの席数と年間の売上高のデータがあるとします。

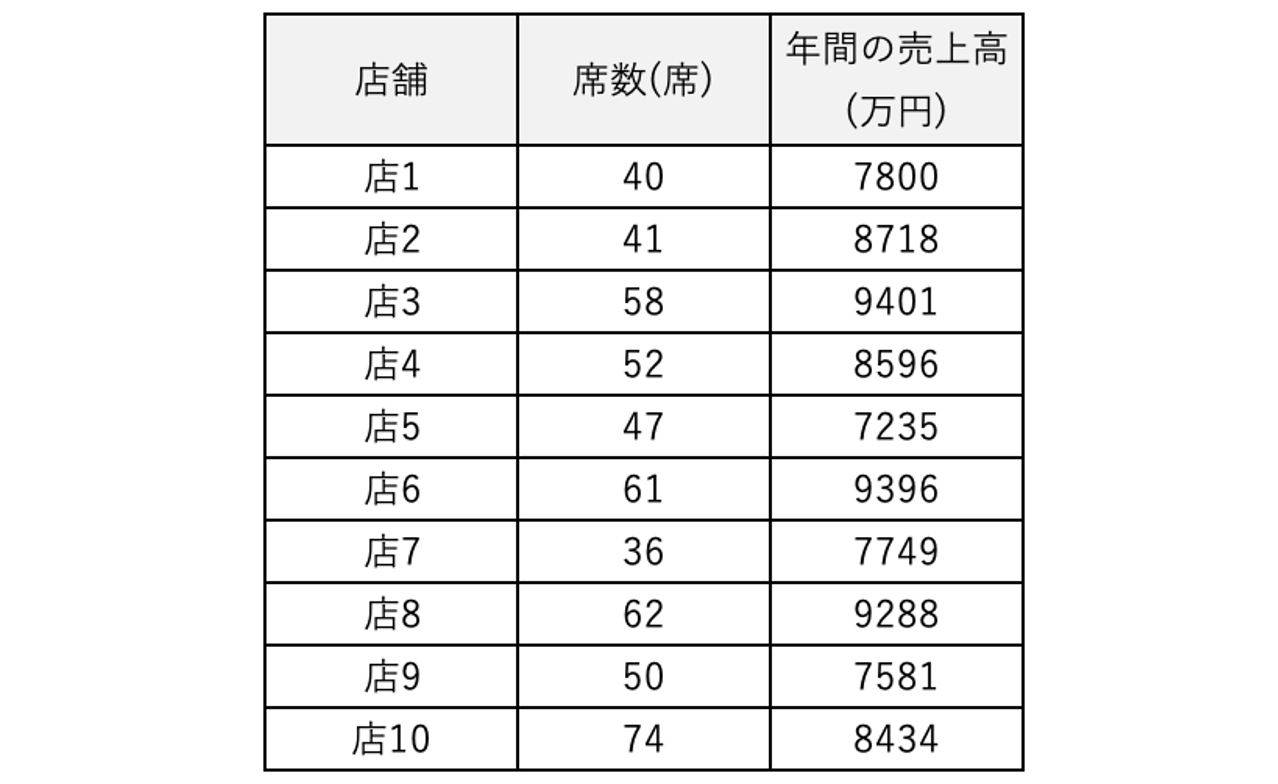
今回は年間の売上高を目的変数、席数を説明変数として回帰分析をすると、2つの関係を最適に捉える下記の式が導かれます。

回帰分析の結果として得られる式を”回帰式”と呼び、回帰分析は式の係数と切片の値を推定して目的変数と説明変数の関係を表します。この例の回帰式からは、席数は1つ増えると年間売上を37万円増加させる関係であると読み取ることができます。

このように、回帰分析によって説明変数が目的変数にどの程度の影響を与えているかを知ることができます。また、回帰分析には下記の通り2種類あります。

• 単回帰分析
• 重回帰分析

回帰分析に関してはこちらの記事で詳しく解説しています。「係数」や「切片」などの用語の意味をしっかり押さえたい方は、まずこちらで基礎的な概念を理解しましょう！

回帰分析とは？目的やExcelでのやり方までわかりやすく解説！

1-2.単回帰分析と重回帰分析の違い

単回帰分析と重回帰分析の違いは、分析に使用する要素の個数です。

単回帰分析

単回帰分析は、1つの説明変数が目的変数に与える影響度合いを分析する手法です。先のカフェチェーンの例で示したものが、これにあたります。

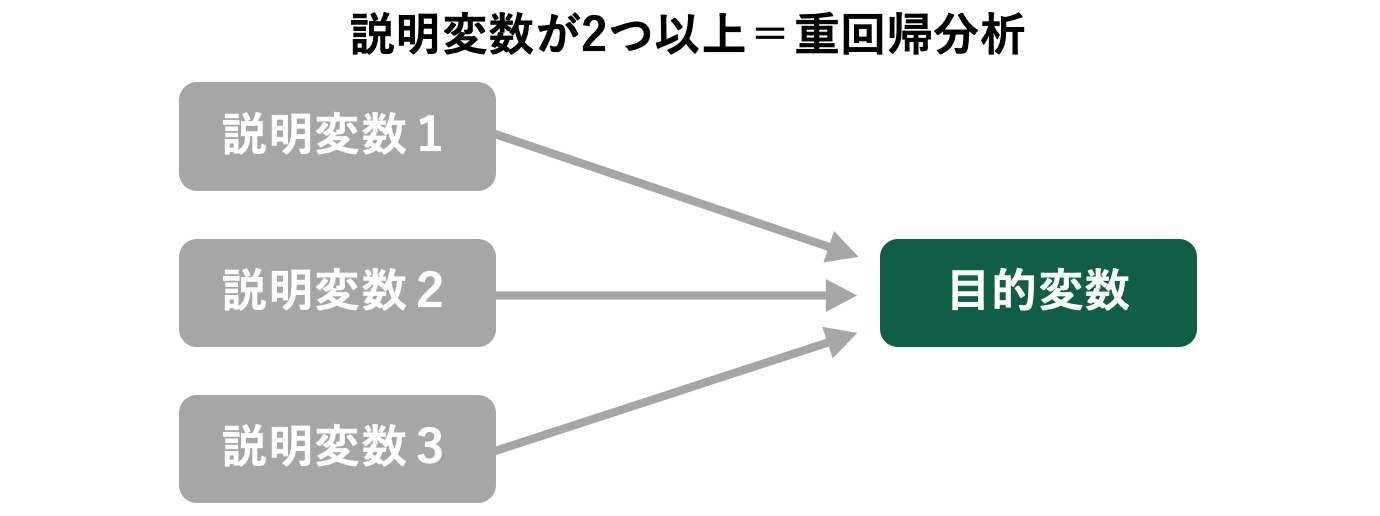
重回帰分析

重回帰分析は、2つ以上の説明変数が目的変数に与える影響度合いを分析する手法です。統計学における「重」という言葉には「複数の」という意味があります。

1-3.重回帰分析の使用例

重回帰分析のイメージを掴みやすくするために、同じくカフェチェーンの例で詳しくみていきましょう。下記のように「席数」「最寄駅からの徒歩時間」「モーニングサービスの有無」「年間の売上高」のデータが存在するとします。

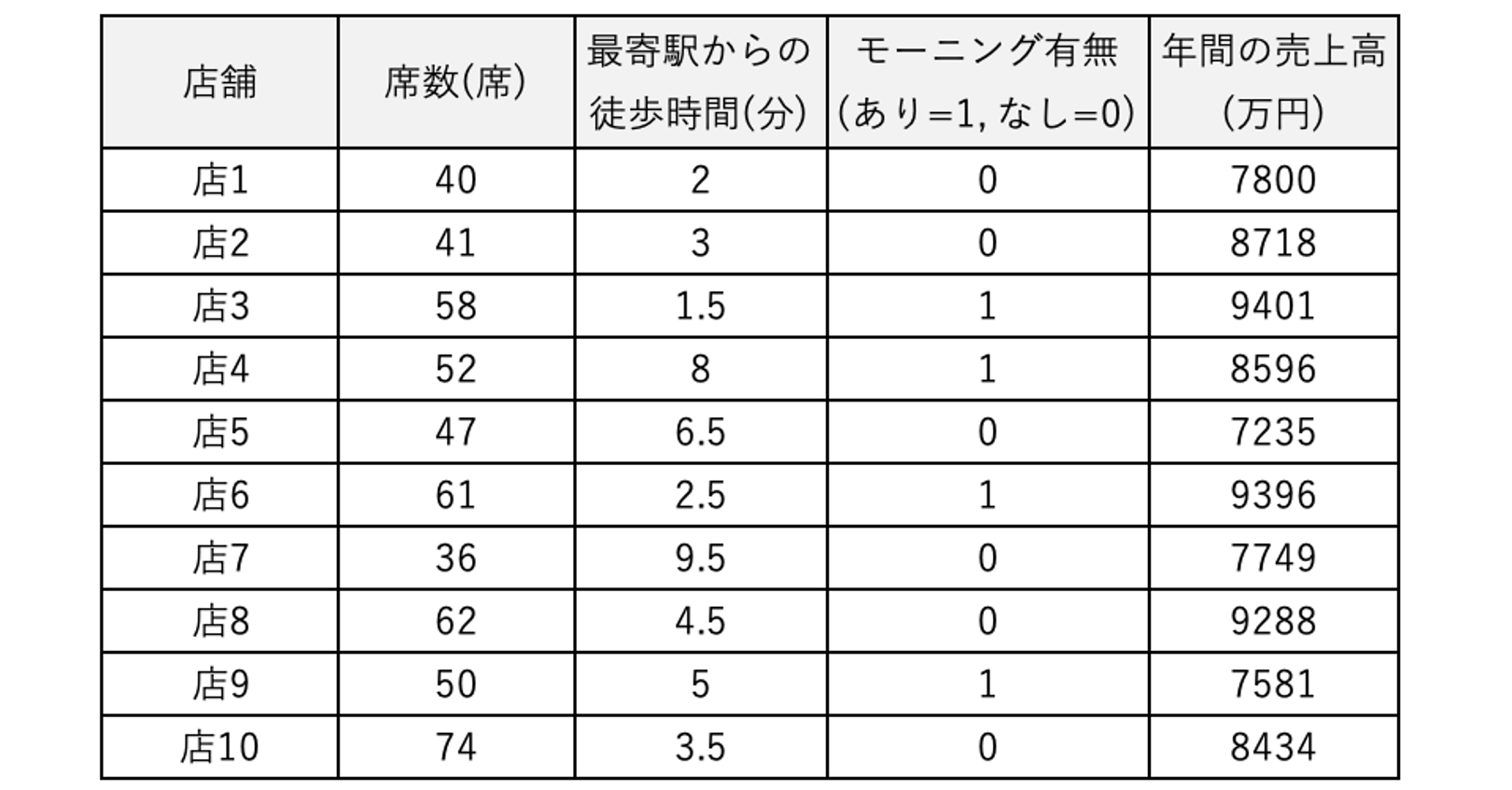
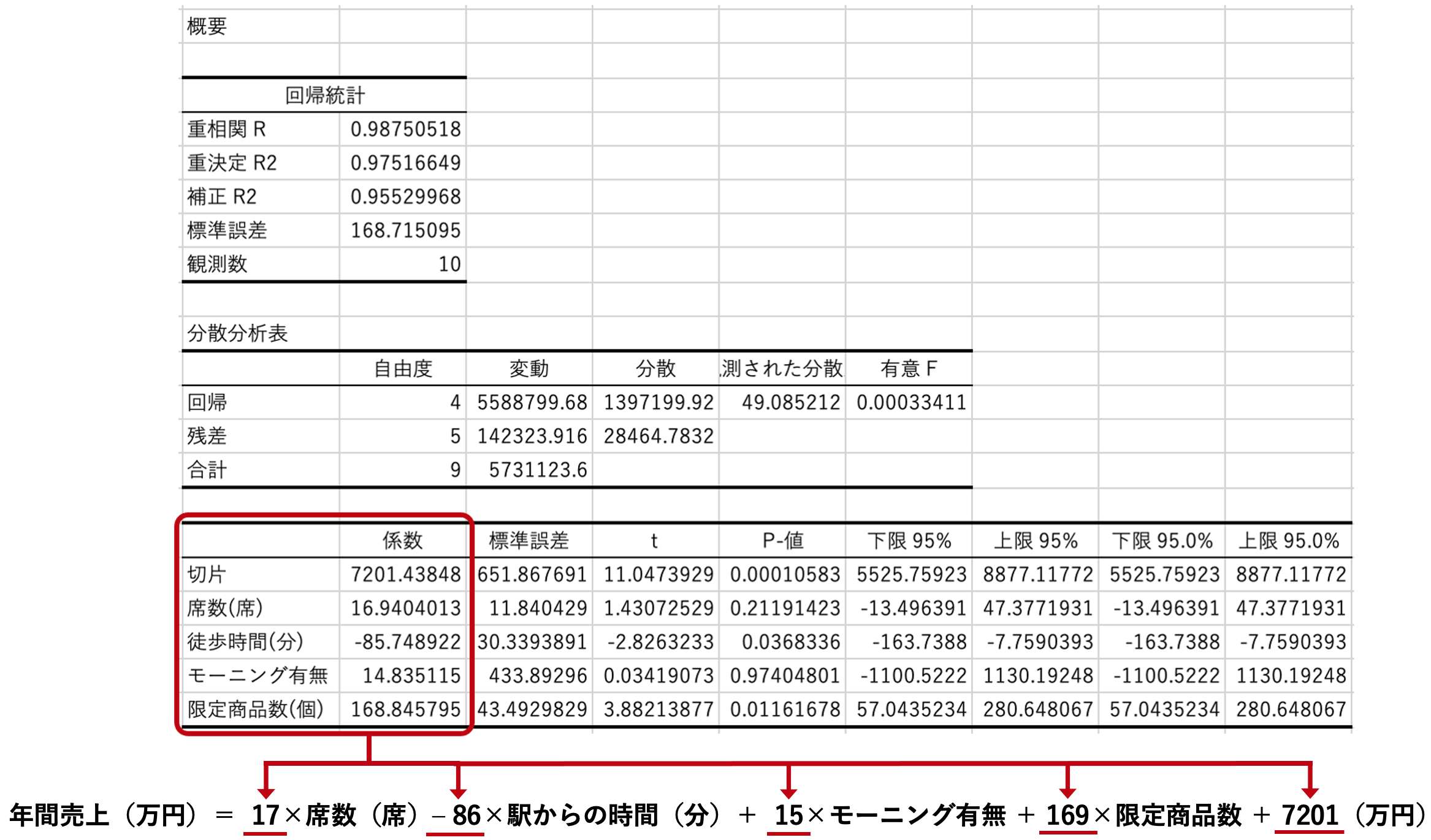
年間の売上高を目的変数、その他の3つを説明変数として重回帰分析をすると、4つの関係を最適に捉える下記の式が導かれます。

上記の回帰式から、次のような関係を読み取ることができます。

• 席が1つ増えると、売上が25万円増える
• 駅からの徒歩時間が1分増えると、売上が100万円少なくなる
• モーニングサービスがある場合はない場合と比べ、売上が350万円増える

このように、重回帰分析によって複数の説明変数が目的変数にどの程度の影響を与えているかを知ることができます。

1-4.重回帰分析でできる2つのこと

重回帰分析の使いどころは、”ある成果の要因を分析をしたいとき”や”ある成果の予測をしたいとき”です。

要因分析をする

前述した通り、重回帰分析で推定された係数の値から各説明変数の影響度を測ることができます。加えて、それぞれの説明変数の係数に着目して大小を比較することで、目的変数に最も高い影響を与える説明変数を探ることも可能です。

カフェチェーンの回帰式の係数に着目すると、モーニングサービスを実施しているか否かが一番大きく売上に影響を与えていることがわかります。

重回帰分析には、ある成果を上げるために重要視すべき要素を把握できる利点があります。その重要な要素が与える影響度とその改善実行に必要なコストを比較し、施策を練ることにも活用できます。

予測分析をする

重回帰分析によって得られた回帰式の各説明変数へ別の数値を当てはめることで、目的変数の値を予測することができます。例えばカフェチェーンで新店舗を構える際、検討中の席数・最寄駅からの徒歩時間・モーニングサービスの有無を回帰式に当てはめると、おおよその年間売上を予測することが可能です。

DXのお悩みを解決する「DXの羅針盤」をダウンロードする

2.重回帰分析の流れ

2章では、重回帰分析を実施する際の具体的な流れについて解説します。今回は、下記のカフェチェーンのデータを分析するとします。

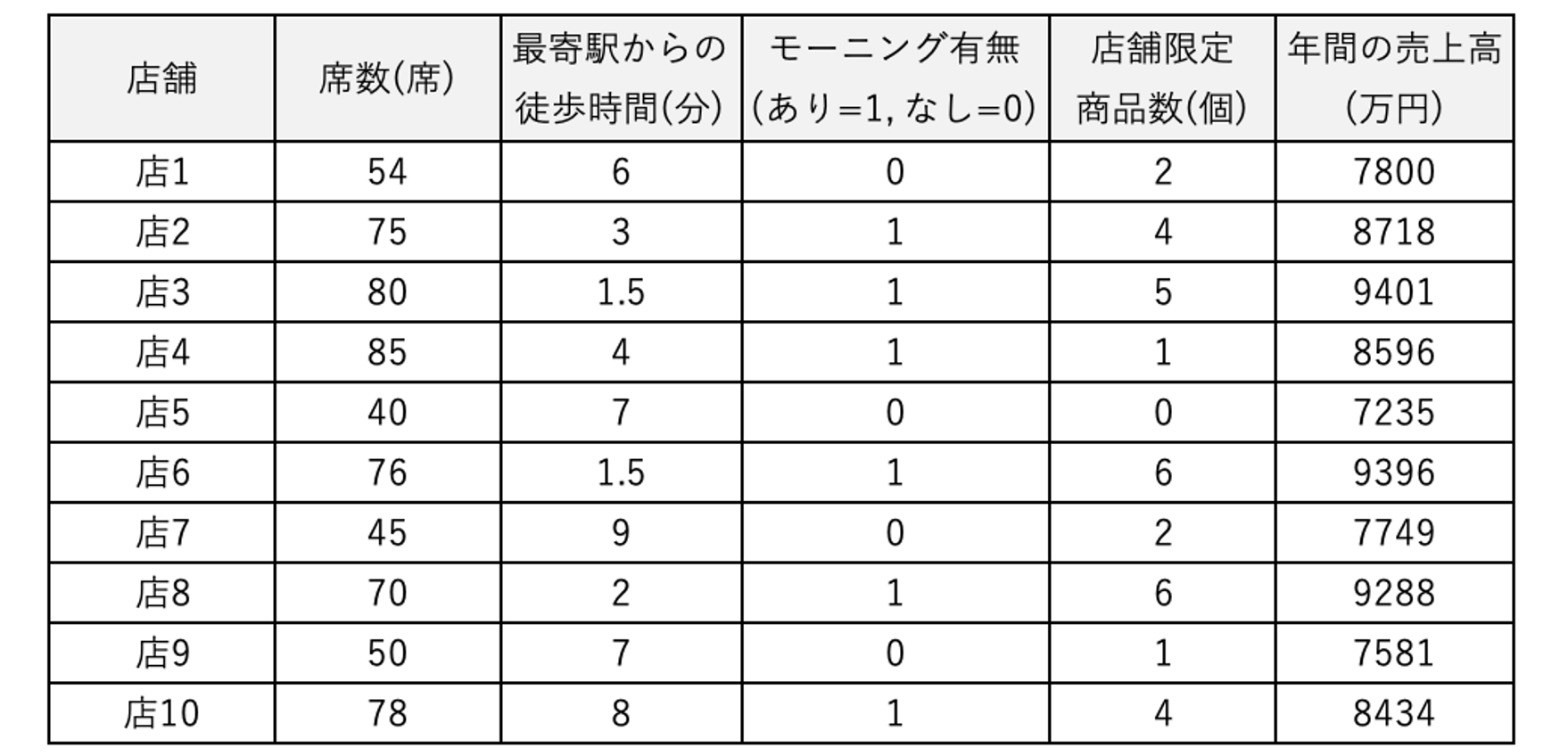
2-1.目的変数とそれに関係していそうな説明変数を決定する

まず初めに、下記のように目的変数と説明変数を定めます。

1. 分析対象のデータから要因・予測分析を行いたい目的変数を決定します。
2. 定めた目的変数に影響を与えていそうな説明変数を洗い出し、決定します。このとき、データ行を区別するための行IDなどは明らかに目的変数の値変動を左右するデータではないと判断できるため、分析から除外します。

今回は、目的変数を年間の売上高に設定し、その他を説明変数とします。このとき、「店1」や「店2」というような店舗を区別するデータは売上高を左右しないため、分析からは除外します。よって、分析データは下記の通りとします。

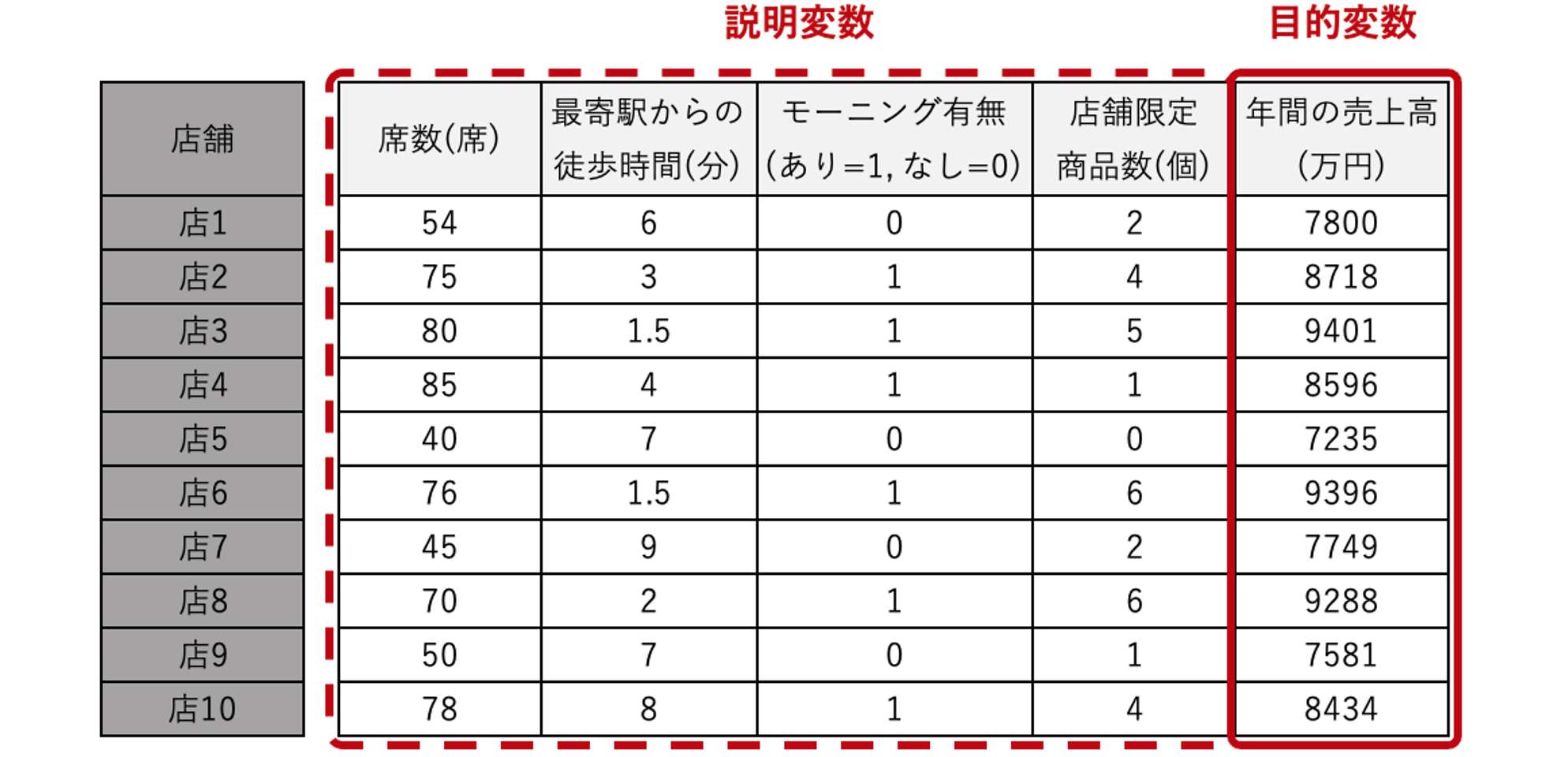
2-2.回帰式を推定する

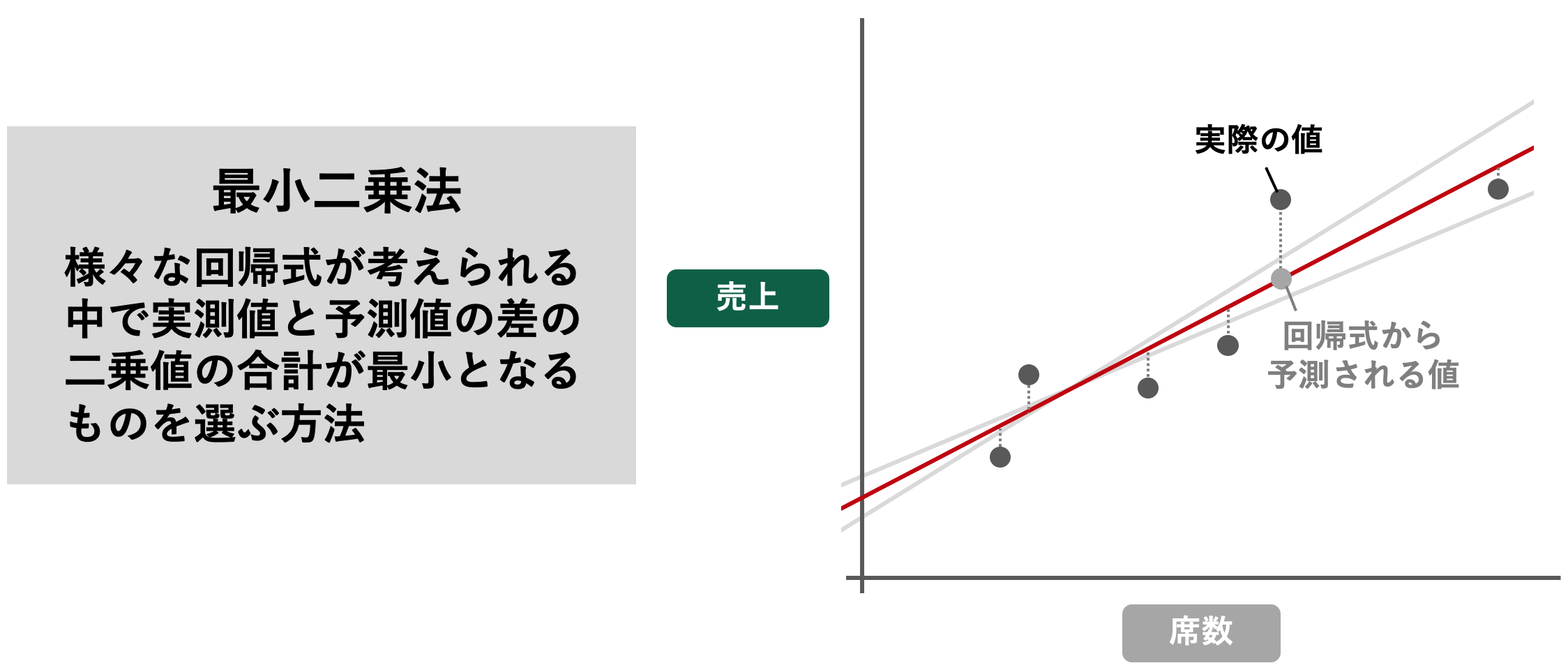
回帰分析では、データの関係を最適に捉える回帰式を推定しようとします。つまり、回帰式を構成する係数と切片を最適に算出することが重要になります。算出方法の一つとして”最小二乗法”があります。最小二乗法などの推定方法は少し難しいため詳細な解説は省きますが、Excelなどのツールを使用して分析を行う際は、推定方法を意識しなくても分析に支障はありません。

最小二乗法を一言で説明すると、実際の各値と回帰式によって予測される値の差の二乗値の合計が最小となるように係数と切片を算出する方法です。

2-3.回帰式の評価をする

推定された回帰式の妥当性を評価します。後の要因・予測分析に使用しても良いものかをこの評価によって確認できます。3章で評価方法について詳しく解説します。

3.分析結果の見方

重回帰分析を行うと、結果として決定係数やt値などの様々な値が表示されます。これらは回帰式を構成する値と分析結果を評価するために使う指標に分けられます。

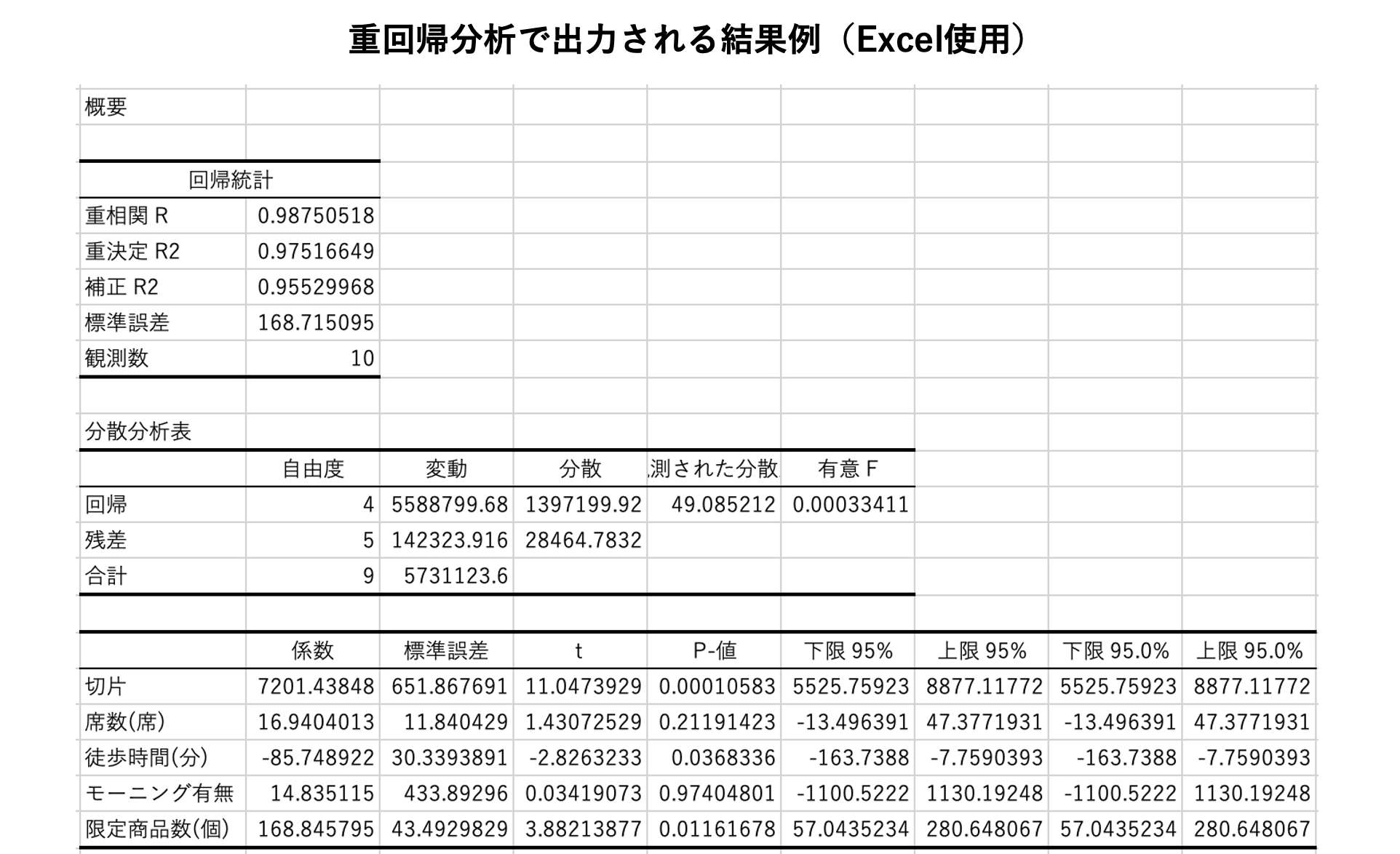
回帰式

回帰式は分析結果の”係数”から組み立てることができます。係数は他の変数の影響を除去した後の当該変数の影響の大きさを示します。

分析結果の評価

分析結果を評価する指標は多くありますが、評価の観点は大きく分けて4つあります。

• 推定された回帰式の精度をみる
• 推定された回帰式が統計的に意味があるかをみる
• 推定された係数が統計的に意味があるかをみる
• 各説明変数の影響度をみる

3-1.推定された回帰式の精度をみる

推定された回帰式を要因・予測分析に活用する前に、目的変数の値変動を説明変数によってどの程度説明できているかを確認します。精度の悪い回帰式をその後の分析に用いるのを防ぐ目的があります。

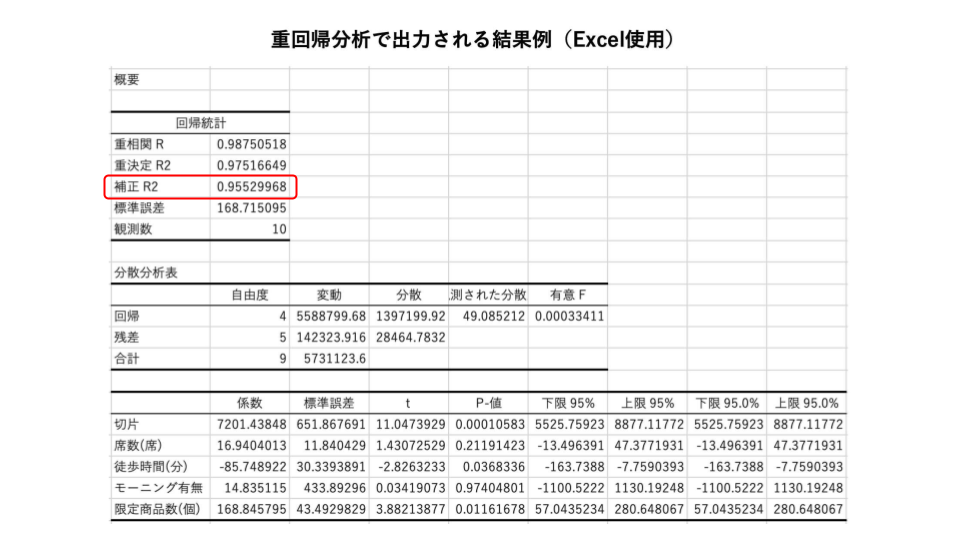
回帰式の精度をみるには、“補正R2”の値を確認します。補正R2は0から1の範囲で値をとり、0に近いほど低く、1に近いほど高い精度の回帰式と判断できます。

3-2.推定された回帰式が統計的に意味があるかをみる

推定された回帰式が統計的に意味があるものかを確認します。

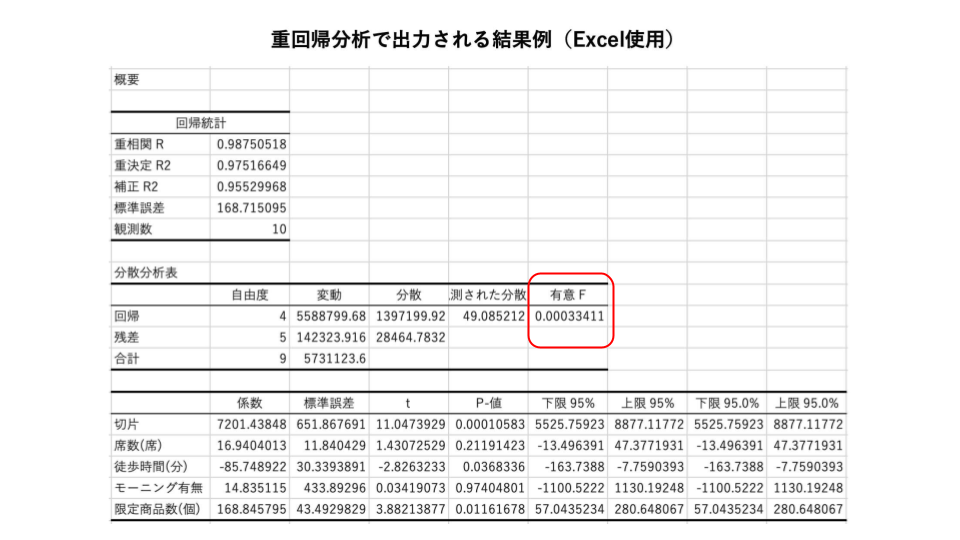
回帰式の有意性をみるには“有意F”を確認します。一般的に有意Fが0.05未満であれば、有用な回帰式を得られたと判断できます。一般的な0.05未満であれば良いとしましたが、実際にはこの水準は自身で定めることができ、0.05もしくは0.01を設定することが殆どです。

3-3.推定された係数が統計的に意味があるかをみる

推定された係数が統計的に意味があるものかを確認します。

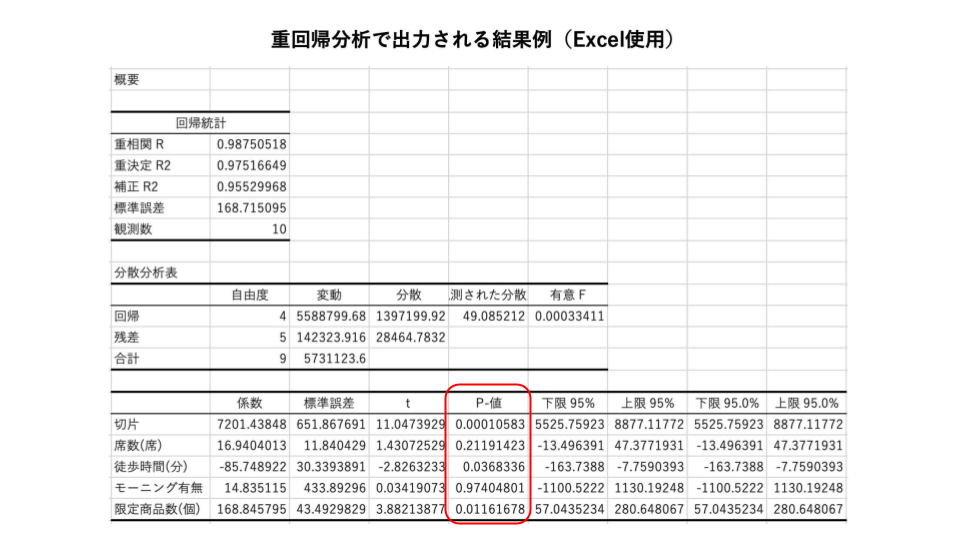
係数の有意性をみるには“P-値”を確認します。一般的にP-値が0.05未満であれば、その説明変数は目的変数に対して「関係性がある」という判断をします。0.05以上の場合は「関係がない」と捉えることができます。値が大きい係数は重回帰分析から除外していく対象になります。この一般的な水準0.05は有意Fと同じように自身で定めることができ、0.05もしくは0.01を設定することが殆どです。

3-4.各説明変数の影響度をみる

各説明変数の影響度を確認します。

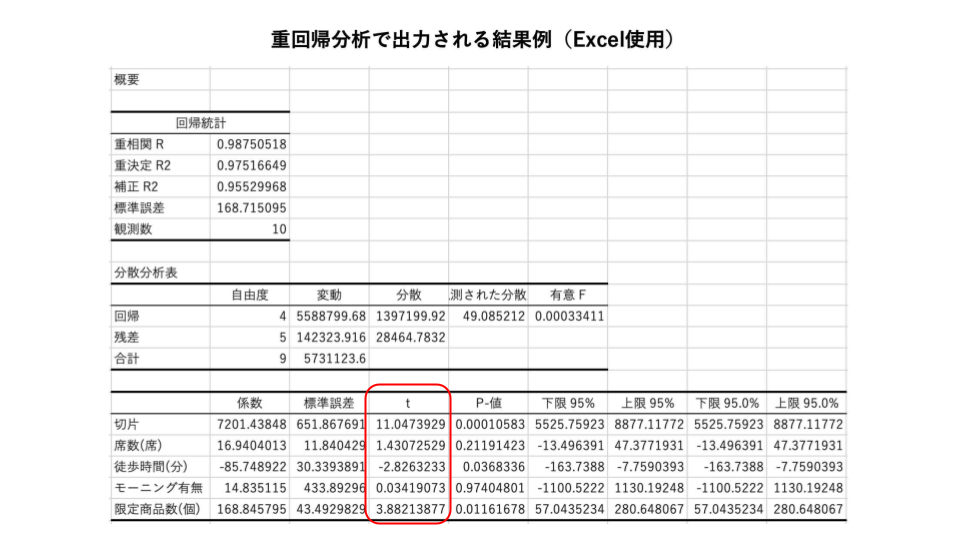
説明変数の影響度をみるには、“t値”を確認します。t値はそれぞれの説明変数が目的変数に与える影響の大きさを表し、絶対値が大きいほど影響が強いことを意味します。目安としてt値の絶対値が2より小さい場合は、統計的にその説明変数は目的変数に影響しないと判断します。

※R2や有意Fなどの用語は、弊社オウンドメディア記事「回帰分析とは？目的やExcelでのやり方までわかりやすく解説！」にて詳細を解説しているため、合わせて読んでいただくことで理解が深まります。

4.Excelでカンタンにできる重回帰分析のステップ

具体的な重回帰分析の実施方法について解説します。本稿では多くの方が使用できるExcelを使用した分析を実践します。しかし、重回帰分析はExcelのほかSPSSやExploratoryなど、みなさんがお持ちのツールでも行うことができます。

Excelの「分析ツール」機能の詳細は、「今すぐ使える！Excelの「分析ツール」機能で始めるデータ分析」も合わせてご一読ください。

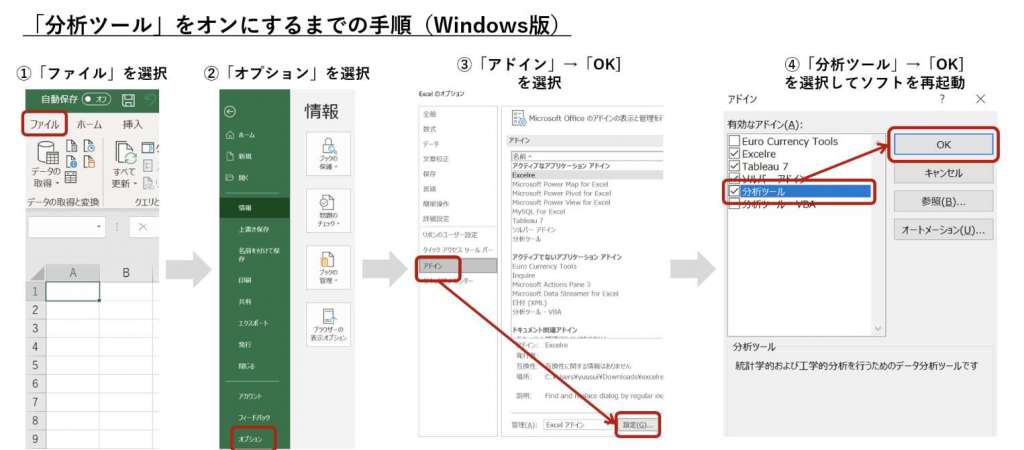
4-1.ステップ1 Excelの「分析ツール」機能を導入する

Excelで重回帰分析など統計的な分析を行うには、”分析ツール”という機能を使えるようにする必要があります。分析ツールとはExcelのアドインの1つで、クリックや簡単なパラメータ入力のみでデータ分析を可能にする機能です。

本稿ではWindows版の導入方法を解説します。WindowsとMacでは導入方法が若干異なるので、Macの方はこちらで導入方法を参照してみてください。（キャプチャではExcel2016を使用したものを掲載しています。）

【導入手順（Windows版）】

1. エクセルを開いた画面から「ファイル」を選択
2. 左端のバーから「オプション」を選択
3. 新しく開いたウィンドウで、「アドイン」→「設定」を選択
4. さらに開いたウィンドウで、「分析ツール」にチェックを付け「OK」をクリック、ソフトを一度閉じ再び開く

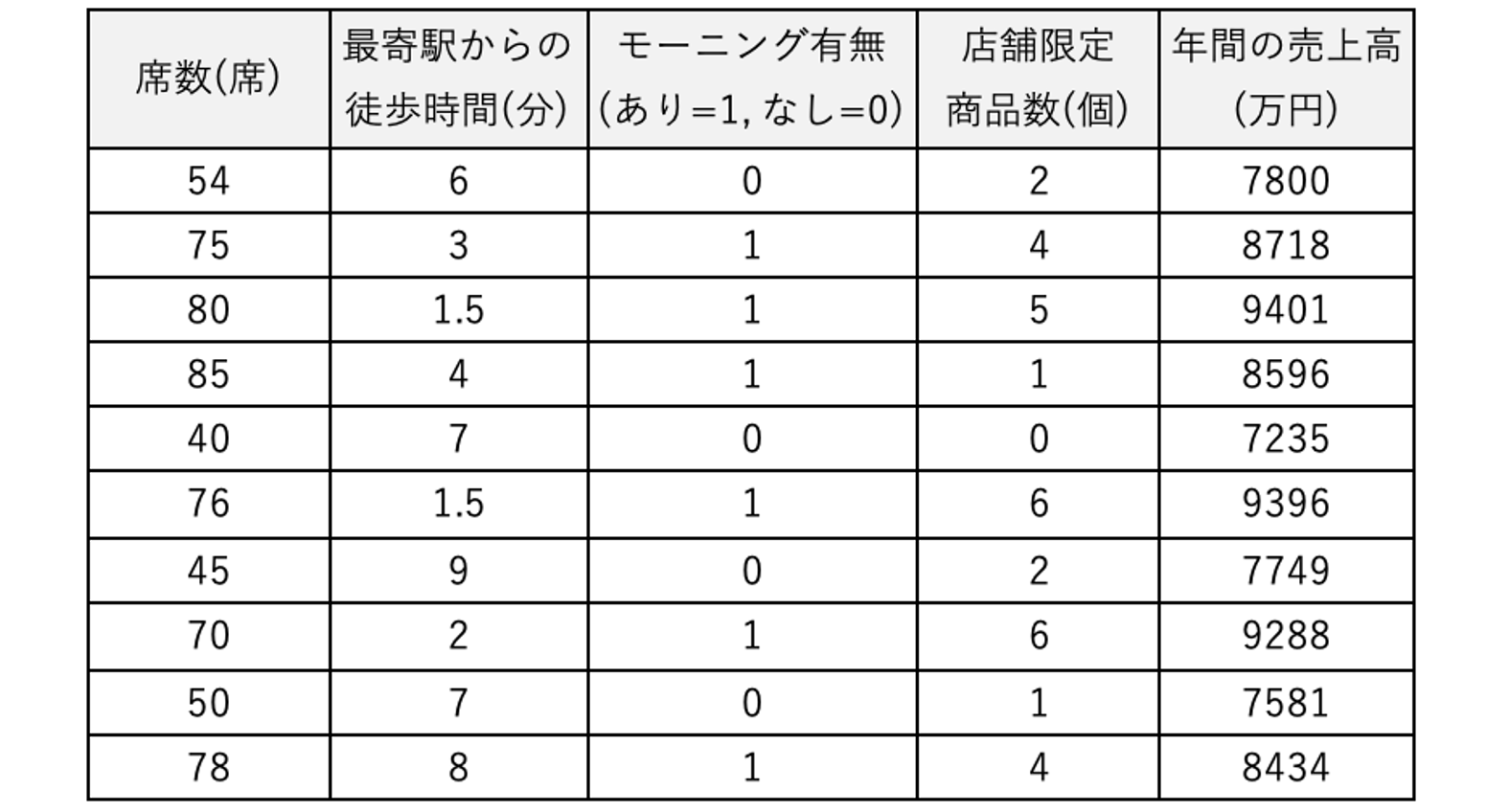
4-2.ステップ2 分析データを用意する

分析するデータを用意します。目的変数とそれに影響を与えていそうな説明変数を抽出したものです。本稿では下記のデータを使用します。

4-3.ステップ3 分析ツールで回帰分析を設定する

リボンの「データ」から「データ分析」を選択し、開いたダイアログで「回帰分析」を選択します。

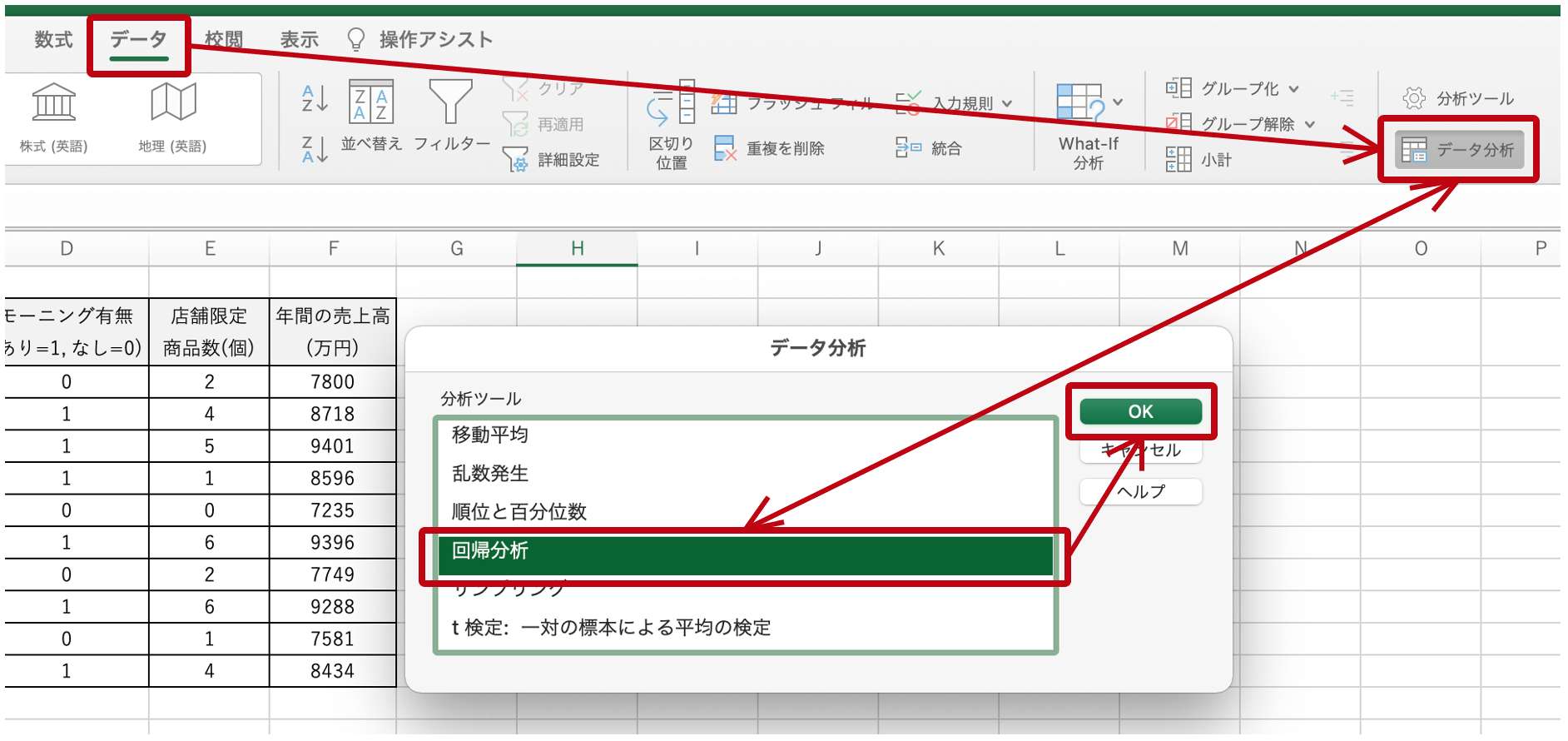
次に表示されるダイアログで以下の設定を行います。

• 入力Y範囲：分析対象の目的変数の範囲を指定します
• 入力X範囲：説明変数の範囲を指定します
• ラベル：上で指定した範囲にデータ名を含めた際はチェックを入れます
• 出力オプション：分析結果の出力先をお好みで設定します

ダイアログの「OK」をクリックすると、結果が出力されます。

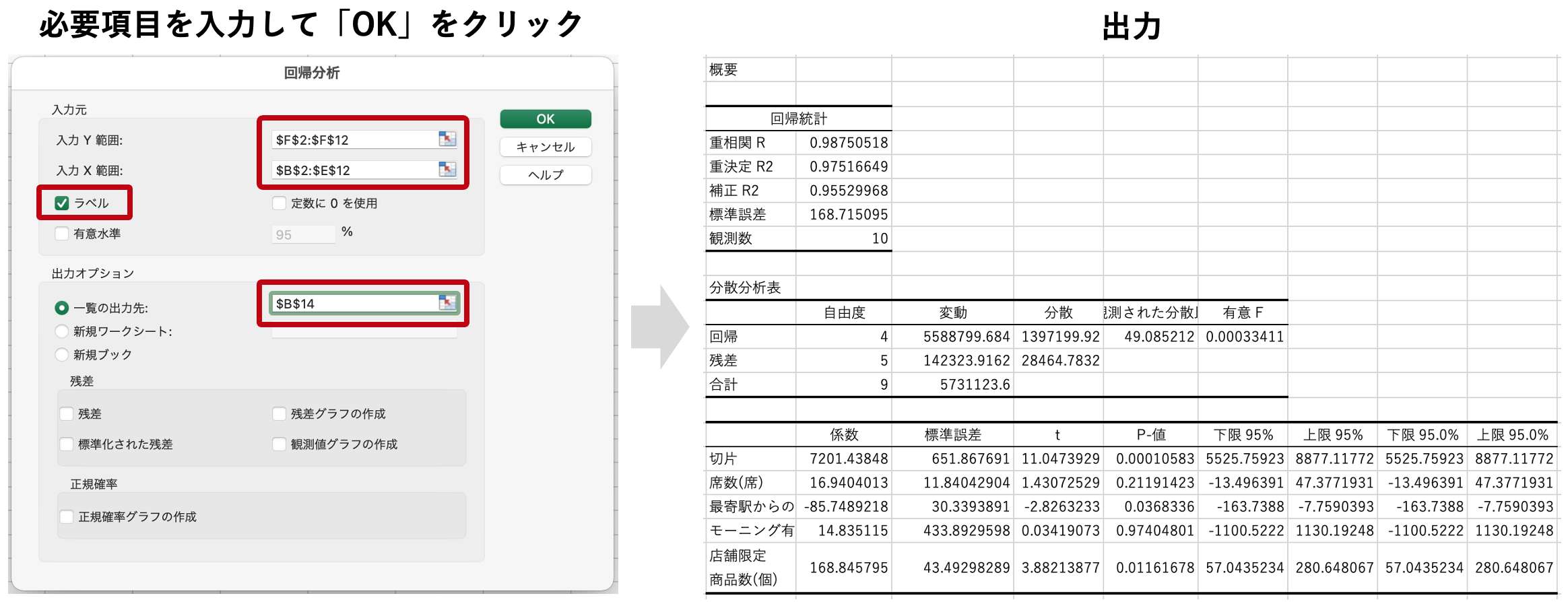
4-4.ステップ４ 分析結果を解釈する

出力された値を使用して、分析結果の評価を行います。

推定された回帰式の精度をみる

回帰式の精度をみるために決定係数である補正R2値を確認すると、0.96であることがわかります。これは推定された回帰式が売上変動の96％を説明できていることを表すので、良い精度の回帰式が得られたといえます。

推定された回帰式が統計的に意味があるかをみる

回帰式の有意性をみるために有意Fを確認すると、0.0003ととても小さい値であることがわかります。一般的な水準の0.05未満という条件を満たしているので、推定された回帰式が有用なものであるといえます。

推定された係数が統計的に意味があるかをみる

係数の有意性をみるためにP-値を確認すると、最寄駅からの徒歩時間と店舗限定商品数のP-値が一般的な水準の0.05未満という条件を満たしていることがわかります。その他の説明変数のP-値は0.05を上回っています。そのため、今回の分析において席数とモーニングサービスの有無を売上に影響を与える要素として考えるのは危険だという判断ができます。

各説明変数の影響度をみる

最後に、推定係数が有意だった最寄駅からの徒歩時間と店舗限定商品数の2つの説明変数の影響度をみるため、t値を確認します。最寄駅からの徒歩時間のt値の絶対値は2.8、店舗限定商品数のt値の絶対値は3.9です。このことから、売上に最も影響を与えている要素は店舗限定商品数であると結論付けることができます。

5.重回帰分析の分析前に気をつけるべき4つのポイント

4章までで重回帰分析の基礎から実践までを理解いただきました。5章では実際に重回帰分析するにあたって注意すべき点について解説します。注意する点は多くありますが、初心者の方に特に気をつけてほしい4つのポイントに絞っています。

5-1.正しい分析手法を選択する

まず初めに、行いたい分析が重回帰分析で良いかを確認しましょう。分析前に分析する変数の種類を考慮し、それに合った正しい手法を選択する必要があります。重回帰分析は、分析に使用する目的変数と説明変数が全て数値データである必要があります。例えば目的変数として「顧客が来店する・しない」のようなデータを設定する場合は、別の分析手法を使用します。

用いる分析手法の選択

分析に用いる目的変数と説明変数の種類によって分析手法が変わるため、正しい手法を選択できるようにしましょう。

5-2.全ての変数を数値データにする

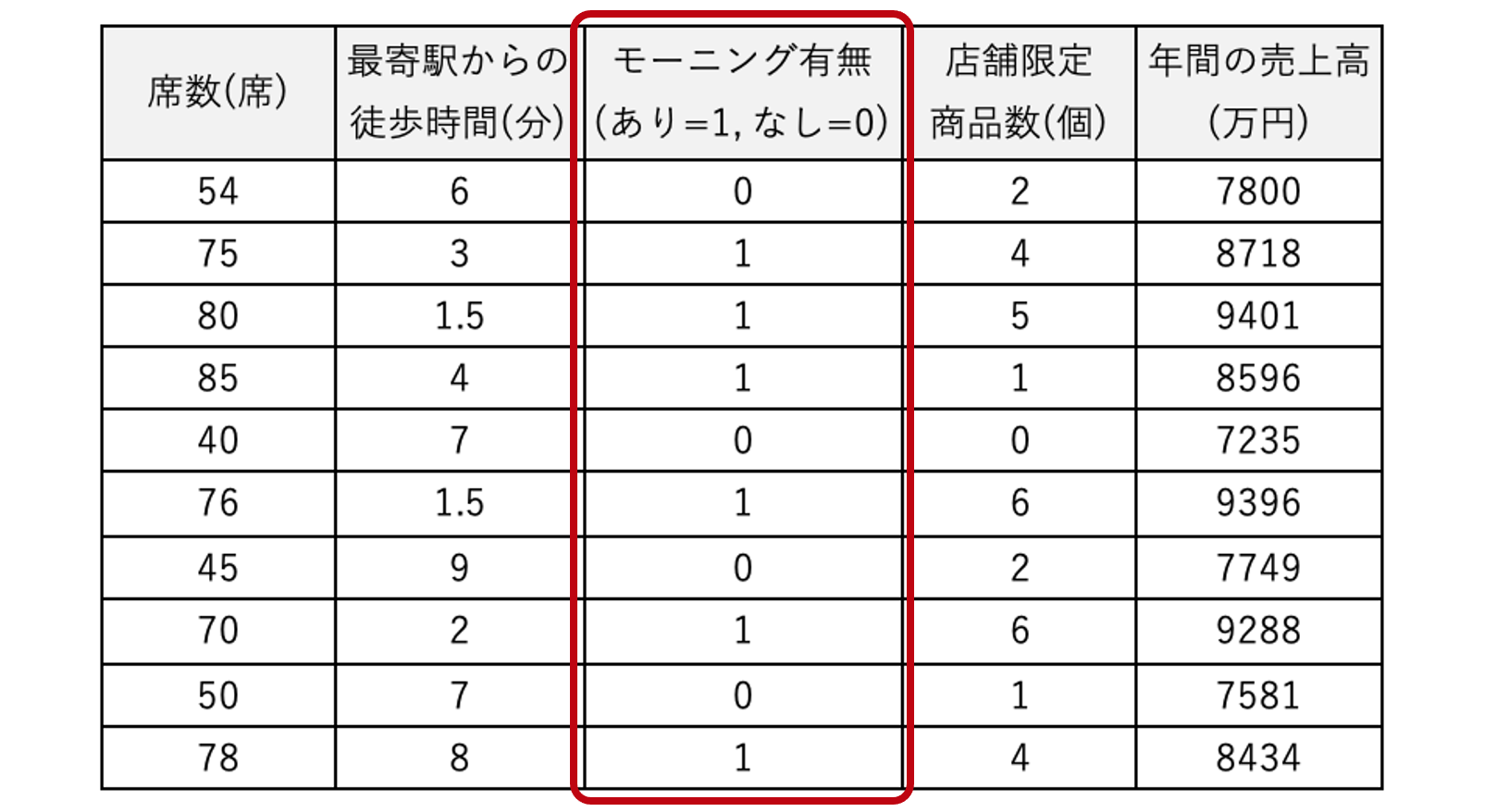
5-1で説明した通り、重回帰分析に使用するデータは全て数値でなればなりません。なぜなら重回帰分析は、値の足し合わせによって目的変数を予測しようとする分析であるためです。よって、分析前に”男性/女性”、”管理職/平社員”のような定性的データを数値に変換する必要があります。定性的データを数量データに置き換えた変数のことをダミー変数と呼びます。

カフェチェーンの例では、モーニングサービスを提供する／しないというデータをそれぞれ、1と0に置き換えて分析を行っています。

5-3.分析に使用する説明変数を厳選する

重回帰分析に使用する説明変数が多いと、適切な結果を得にくくなります。なぜなら説明変数が多くなる分、推定された回帰式の目的変数への当てはまりがどうしても良くなってしまうからです。

目安の説明変数の数は7個程度が良いとされています。重回帰分析を行う利点は、どの変数が大きな影響を与えているかや、一見結果とは相関が弱いのに分析に加えると予測精度が上がるような変数を見出すことです。あまりに多すぎる説明変数を使って分析の質を落とさないように気をつけましょう。

5-4.多重共線性を取り除く

説明変数間に強い関連性があるとき、「多重共線性がある」といいます。多重共線性はmulticollinearityの略でマルチコと呼ばれることもあります。多重共線性がある場合は分析結果の解釈がとても難しくなってしまうため、どちらか一方の変数を分析から除く必要があります。Excelを使っての分析ならば分析ツール機能の“相関”で予め変数間の関連の強さを確認し、多重共線性を取り除いてから重回帰分析を行いましょう。

相関についてはこちらのコンテンツを参考ください。

相関分析とは？分析初心者でもわかる解説とExcelでのやり方を紹介

まとめ

重回帰分析とは、説明変数が目的変数に与える影響度合いを数値として表すもので、要因や予測分析に活用できる手法でした。一見難しく思える分析手法でしたが、ここまで読み進めてみて自分にもできるかもと自信を持っていただけたのではないでしょうか。

まずは身近なデータで重回帰分析を試して十分に理解し、武器として使えるようにしましょう！

その他データ分析の代表的な手法には、こちらにもまとめてありますので、次のステップへ行きたい方はこちらも参考にしてください。

重回帰分析など、データの分析・活用をご検討の場合はデータビズラボへお問い合わせください。
データビズラボでは状況やニーズに合わせた様々なサポートをご提供いたします。

データビズラボへ問い合わせする

データ分析の手法｜代表的な手法25選をイラストでわかりやすく解説