回帰分析とは、求めたい要素の値に対し、他の要素がどの程度影響を与えているかを分析する手法です。売上の予測など、様々な場面で活用されています。
あなたは今、ご自身の業務で扱っているデータを回帰分析を活用することで何か改善につなげられないかと模索されている状態ではないでしょうか?
回帰分析を活用できるようになると、データ分析の活用の幅やデータを根拠とした説明力が飛躍的にアップします。ただ、実際に回帰分析を活用しようとした際に下記のように思うことが多いのではないでしょうか?
- 「回帰分析で何がわかるのだろうか?」
- 「回帰式はどんな目的の際に活用すればいいんだろう、、、」
- 「部下が出した回帰分析結果の解釈の仕方がわからない、、、」
- 「回帰分析と相関分析は何が違う?」
そのため、本記事では初学者が躓きやすいポイントを丁寧に解説しながら、わかりやすく回帰分析について解説をしていきます。本記事を読み終わった頃にはビジネスで回帰分析を使う具体的なイメージが湧いているはずです。
1.回帰分析の概要
まず回帰分析の概要について確認していきます。
1-1.回帰分析とは求めたい要素の値に対し、他の要素がどの程度影響を与えているかを分析する手法
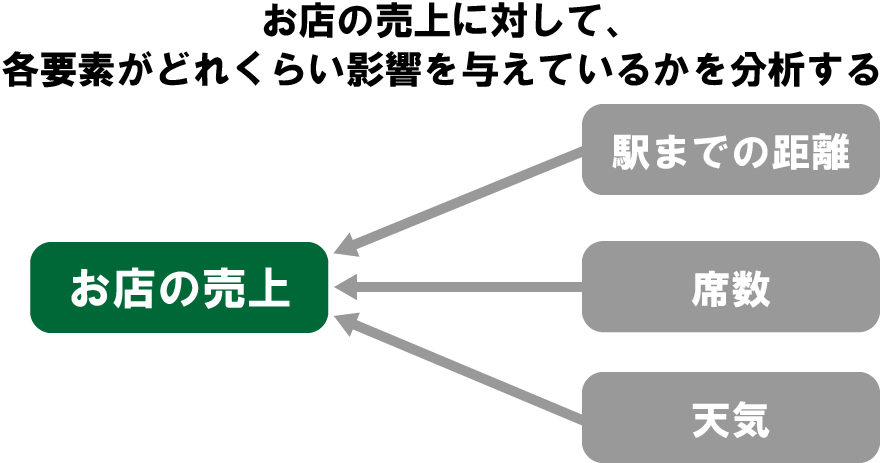
回帰分析とは求めたい要素の値に対し、他の要素がどの程度影響を与えているかを分析する手法です。例えば、お店の売上予測を行いたい場合に下記の要素が売上の数値に影響を与えていそうだ、と考えたとします。
- 駅までの距離
- 席数
- 天気
この場合に、売上の数値を予測するために、「上記の要素がそれぞれどれくらい売上に影響を与えているか?」を分析することが出来るのが回帰分析です。
この回帰分析を深く理解するためには、目的変数と説明変数という概念を理解する必要があります。
1-1-1.目的変数は求めたい要素、説明変数はそれに影響を与える要素
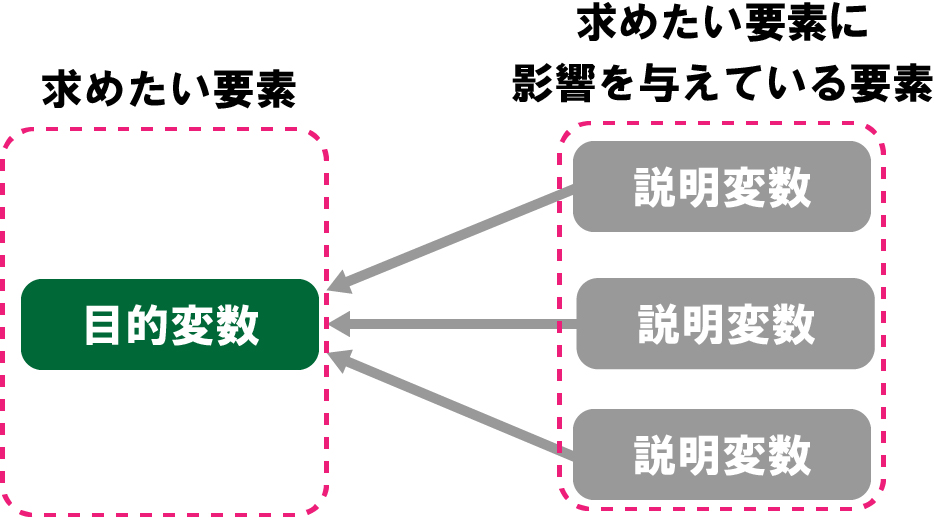
回帰分析では、求めたい要素を「目的変数」、求めたい要素に影響を与える要素を「説明変数」と呼びます。
※目的変数のことを従属変数、説明変数のことを独立変数と呼ぶこともあります。
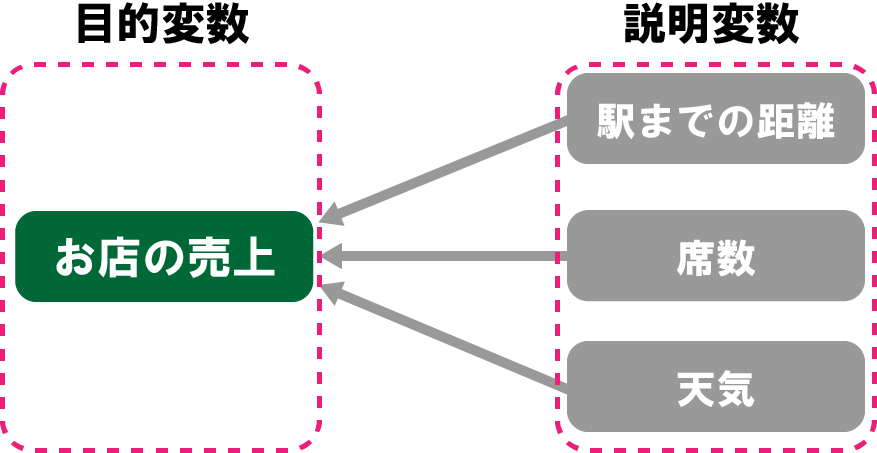
例えば、先ほどの例でお店の売上を下記要素を用いて予測したい場合の目的変数と説明変数の関係は下図のようになります。
- 駅までの距離
- 席数
- 天気
回帰分析では、目的変数に対し、それぞれの説明変数がどの程度影響を与えているかを下記のような数式で表します。
- y= a+bx(説明変数が1つの場合)
- y=a+b1x1+b2x2+,,,+bnxn(説明変数が2つ以上の場合)
ただ、数式だけではわかりにくいと思いますので、あるチェーン店の下記データを使いながら具体的に確認しましょう。
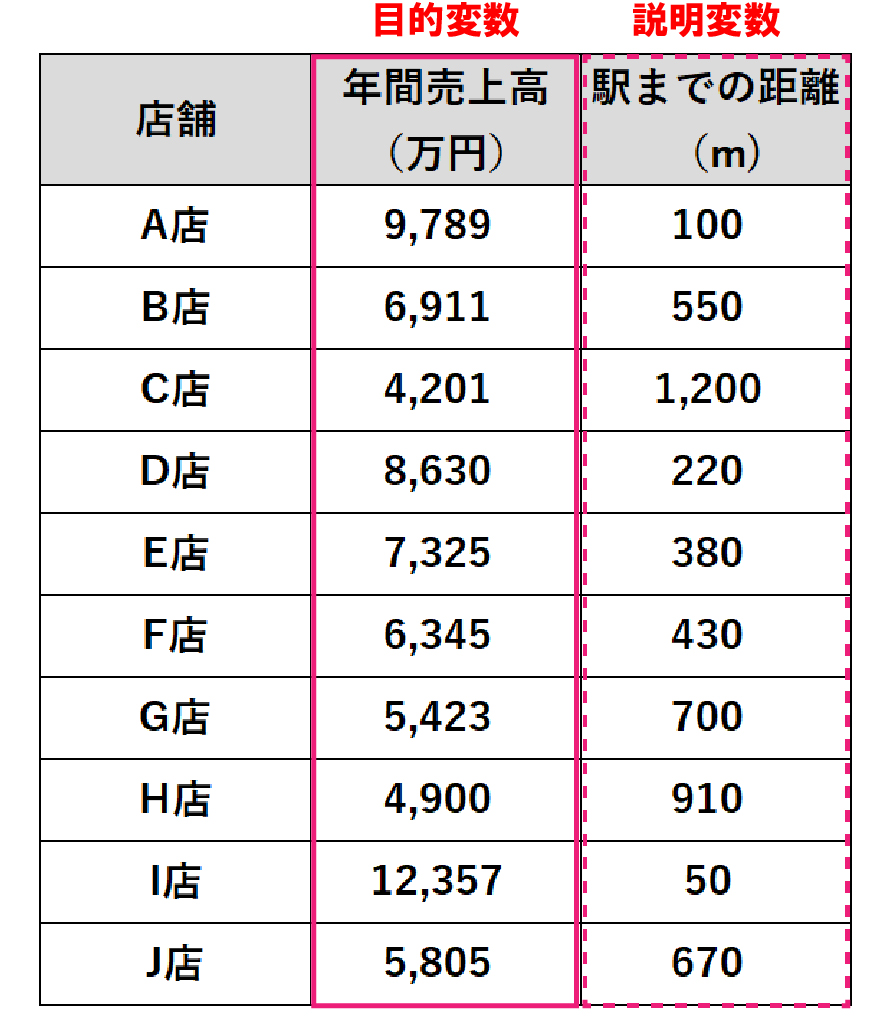
年間の売上高に対して、駅までの距離がどれくらい売上高に影響を与えているかを数値で把握したいとします。予測したい数値は年間売上高になりますので、これが目的変数です。駅までの距離が目的変数に影響を与えている数値なので説明変数となります。
この場合に回帰分析を行い、年間売上高(目的変数)と駅までの距離(説明変数)の2つの関係を数式で表すと下記のような結果となります。
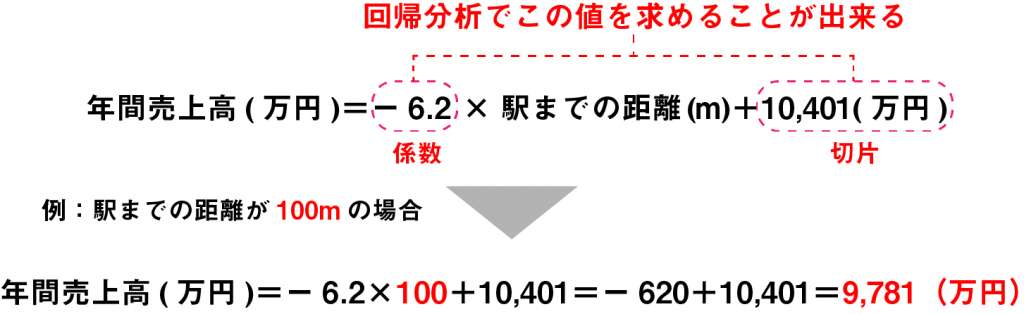
このように回帰分析の結果として得られる式を”回帰式”と呼び、回帰分析は式の係数(回帰係数)と切片の値を推定して目的変数と説明変数の関係を表します。この例の回帰式からは、「駅までの距離が1m増えると年間売上が6.2万円減少する関係」であると読み取ることができます。
1-1-2回帰分析は説明変数の個数により、2種類に分けられる
回帰分析では目的変数の値変動を説明する説明変数の個数により、下記2種類に分けられます。
- 単回帰分析
- 重回帰分析
この単回帰分析と重回帰分析の違いについて簡単に整理しましょう。
1-1-2-1.単回帰分析
単回帰分析は、1つの説明変数が目的変数に与える影響度合いを分析する手法です。前述のチェーン店の例で示したものが、これに該当します。

1-1-2-2.重回帰分析
重回帰分析は、2つ以上の説明変数が目的変数に与える影響度合いを分析する手法です。統計学における「重」という言葉には「複数の」という意味があります。実務で数値予測を行う場合、1つの変数だけが要因として上げられる場合はほとんどないので、主にこちらの重回帰分析が利用されます。
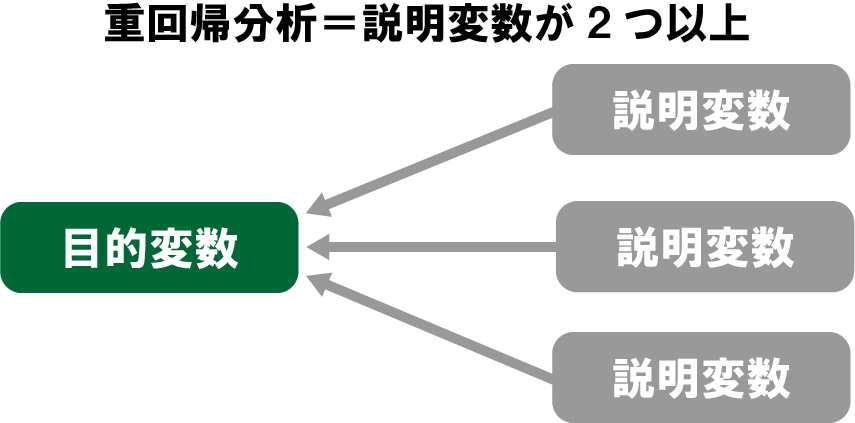
このように目的変数に影響を与える説明変数が1つなのか2つ以上あるのかによって回帰分析の種類が変わることを覚えておいてください。重回帰分析についてはこちらの記事でより詳しく解説していますので、是非ご覧ください。
1-2.回帰分析が主に活用される2つの目的
回帰分析は主に下記2つの目的で活用されます。
- 目的変数の数値を予測する
- 目的変数により大きな影響を与えている説明変数を探る
それぞれ具体的に確認していきましょう。
1-2-1.目的変数の数値を予測する
回帰分析を行う1つ目の目的は目的変数の数値を予測することです。予測をする対象は売上高、利用者数、サイトアクセス数などのビジネスを行う上で重要な指標となる数値が多いです。
回帰分析を行うことで得られた回帰式の各説明変数に別の値を当てはめることで目的変数の値を予測することが出来ます。例えば、前述のチェーン店の例で、駅までの距離が500mの店舗を新たに出店する場合、先ほど得られた回帰式に当てはめることでおおよその年間売上高を予測することが出来ます。
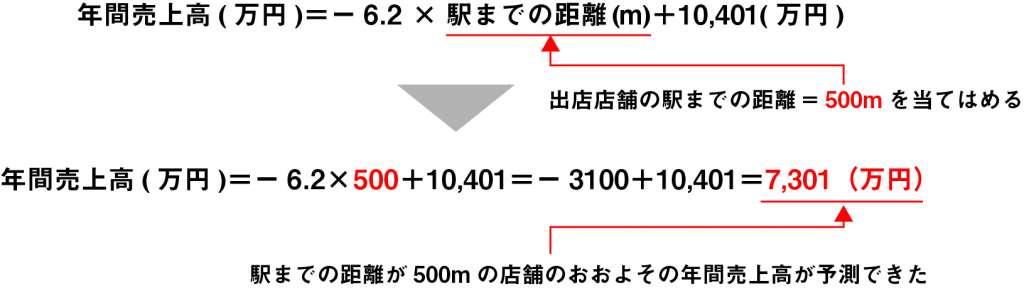
※今回は説明変数が1つの単回帰式であるため、予測精度はかなり低いと思われます。
1-2-2.目的変数により大きな影響を与えている説明変数を探る
回帰分析を行う2つ目の目的は目的変数により大きな影響を与えている説明変数を探ることです。重回帰分析を行うと、複数の説明変数が目的変数にどのように影響を与えているかを数値で把握することが出来ます。例としてチェーン店の年間売上高を目的変数、下記の項目を説明変数として重回帰分析を行う場合を上げます。
- 席数
- 駐車場の台数
重回帰分析の結果、得られた回帰式は下記です。

この回帰式から席数の方が駐車場の台数よりもチェーン店の年間売上高に大きな影響を与えていることがわかります。
このように回帰分析(重回帰分析)を行うことで、「目的変数の値の改善のためにどの説明変数を重要視すべきか?」を把握できることができます。
※複数の説明変数の内、どれが目的変数により大きな影響を与えているかを分析するため、説明変数が1つの単回帰分析はこの目的では使用できません。
2.回帰分析の流れ
では、この章では回帰分析を行う際の具体的な流れについて解説します。本記事は初学者向けの記事になりますので、シンプルな単回帰分析の流れをステップごとに見ていきます。
今回は新店出店を検討しているチェーン店の例に挙げて進めていきます。
2-1.目的変数を決定する
回帰分析を行うには、目的変数を定める必要があります。前述したとおり、目的変数は数値の予測や要因を分析したい要素のことです。チェーン店での目的変数の候補としては下記などが挙げられるでしょう。
- 年間売上高
- 利益
- 来店客数
今回は「新規出店した際の売上がどうなるか?」を予測したいので、年間売上高を目的変数に選びます。
2-2.目的変数に影響を与えていそうな説明変数を決める
次に目的変数に影響を与えていそうな説明変数を決めます。今回は単回帰分析を行うため、選択する説明変数は1つとなります。目的変数に年間売上高を選びましたので、それに関係する説明変数としては下記などが考えられます。
- 席数
- 最寄駅の乗降数
- 最寄駅までの距離
- 店の前の通行量
- 駐車場の台数
今回は日々の店舗運営の中で、売上高に大きく影響していそうだと感じている席数を説明変数とすることとします。
2-3.分析に必要なデータを用意する
目的変数(年間売上高)と説明変数(席数)を決定したら、次に分析に必要なデータを用意します。今回は下記の既存店10店舗の売上高と席数データを使用します。
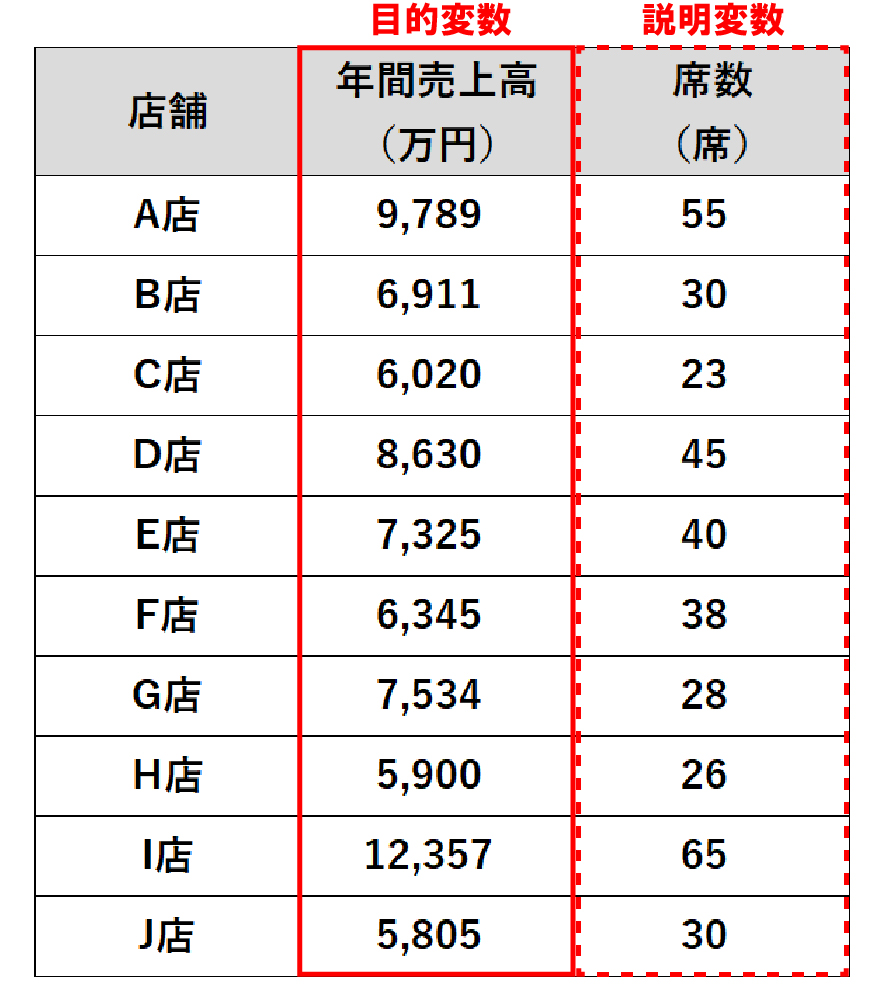
2-4.回帰分析を行い、予測をするための式を求める
必要なデータが用意出来たら、実際に回帰分析を行い、予測をするための式=回帰式を求めます。
回帰分析では、目的変数と説明変数の各データの関係を最適に捉える回帰式を推定しようとします。つまり、回帰式を構成する係数と切片を最適に算出することが重要になります。難しそうに感じますが、Excel等のツールを使って回帰分析を行う場合は簡単に最適な回帰式を求めることが出来ます。
2-3で用意したデータを活用して得られた回帰式は下記です。
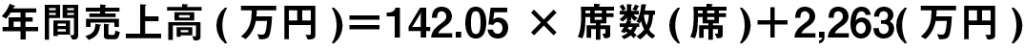
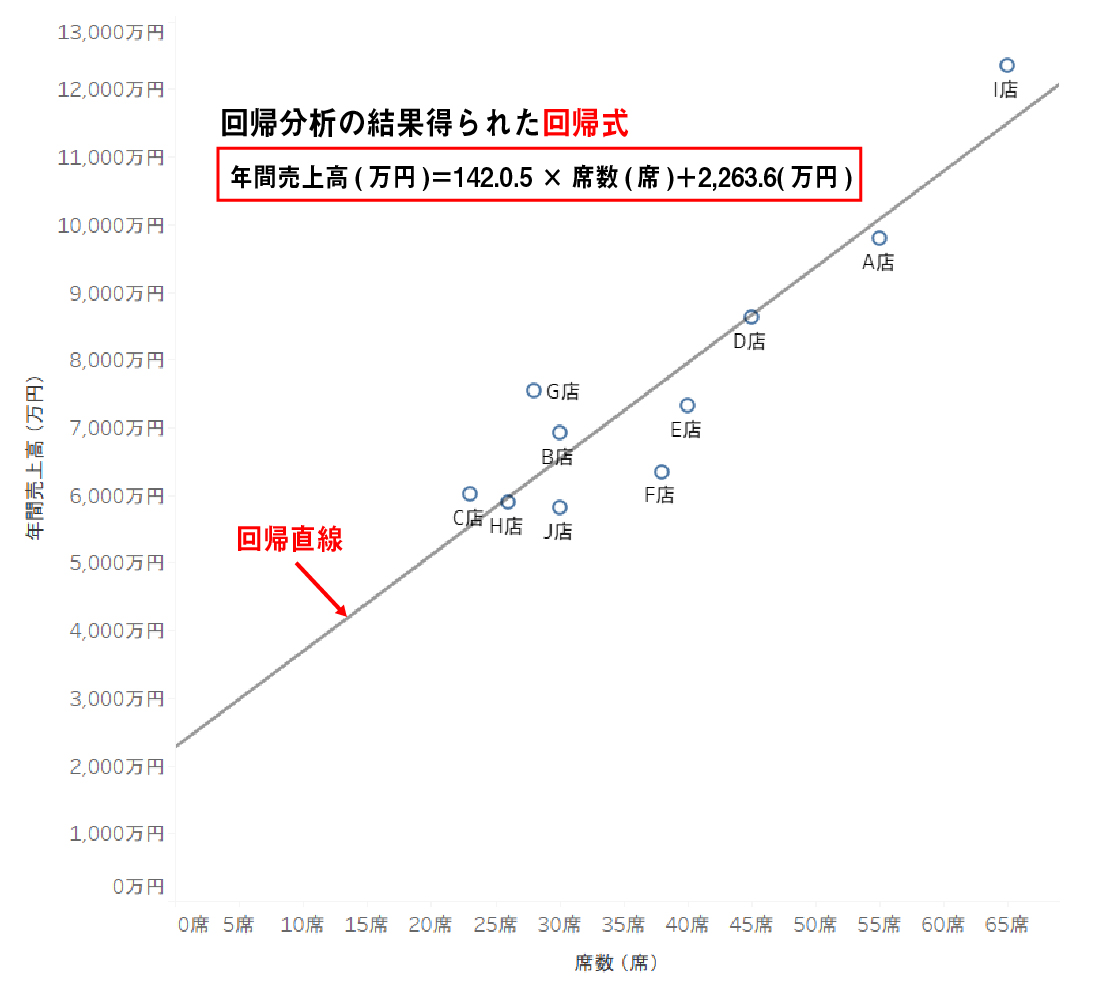
上図は散布図(目的変数を縦軸に説明変数を横軸に配置して各データをプロットした図)ですが、その各データに最もフィットするように引いた直線(これを回帰直線といいます)を一次関数で表したのが回帰式です。
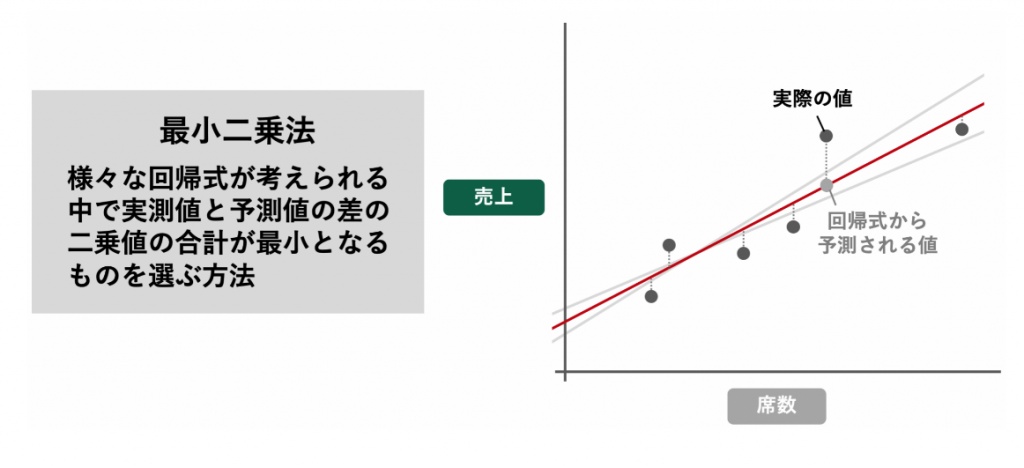
データに最もフィットする直線を引き、係数と切片を最適に算出するための方法の一つとして”最小二乗法”があります。最小二乗法を一言で説明すると、実際の各値と回帰式によって予測される値の差の二乗値の合計が最小となるように係数と切片を算出する方法です。Excelなどのツールを使用して分析を行う際は、推定方法を意識しなくても分析に支障はありませんが、回帰分析を今後使いこなしたい方は是非覚えておいてください。
2-5.回帰式の妥当性を評価をする
回帰分析の結果、回帰式を得られたら、次にその回帰式の妥当性を評価をします。回帰分析を行って得られた回帰式が実務上役に立つどうかを判断するために、回帰式の妥当性を評価することは非常に重要です。なぜ回帰式の妥当性を評価をする必要があるかというと、回帰分析のために使用した目的変数と説明変数のデータによっては、回帰式を得られたとしても、予測精度が低すぎるために全く使えない場合がよくあるからです。
この妥当性の評価を正確に行うためには、回帰分析の結果表示される各指標の意味を把握することが大切です。各指標の意味については次の章で詳しく説明します。
3.回帰分析結果の各指標の意味
回帰式が妥当かどうかを正確に評価するためには「分析結果で表示される各指標が何を意味しているのか?」を理解する必要があります。なぜなら、各指標の意味がわかっていないと回帰分析を行っても、得られた回帰式が有用なのかどうかや、予測にどのように役立つかがわからないからです。回帰分析結果を正しく読み取るために理解しておくべき指標は下記となります。
- 回帰式
- 回帰係数
- 切片
- 決定係数(R2)
- P値
- t 値
例えば、Excelで単回帰分析を行う場合は下記2通りの方法があり、それぞれでの回帰分析の結果が下図のように表示されます。
- 散布図を作成し、「近似曲線の追加」機能で回帰式を表示させる方法
- 分析ツールの「回帰分析」の機能を使う方法
●散布図の「近似曲線の追加」機能での回帰分析の表示
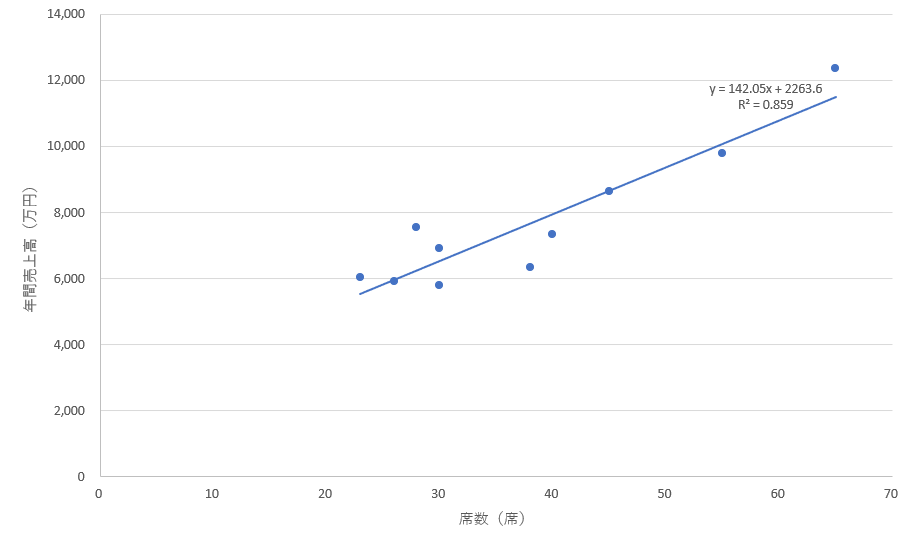
●分析ツールの「回帰分析」での表示
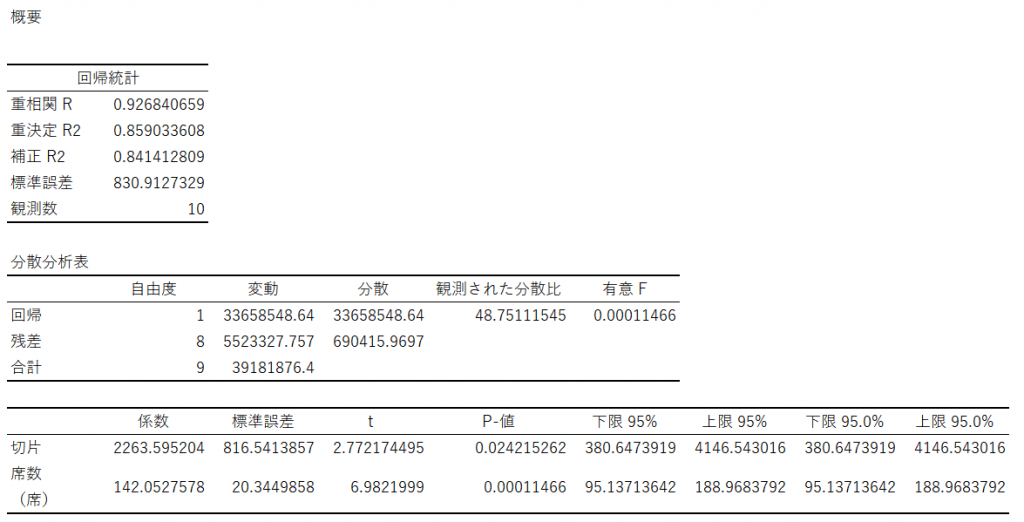
特に分析ツールにおいては、様々な指標が表示されるのがお分かりいただけたと思います。それでは1つ1つ意味を確認していきましょう。
3-1.回帰式
まずは回帰式です。回帰式を理解するためには、回帰係数と切片が何を意味しているのかを知る必要があります。

3-1-1.回帰係数
回帰係数は説明変数の値が1上がった場合に、目的変数がどれくらい増減するかを表しています。
●散布図の「近似曲線の追加」機能での回帰分析の表示
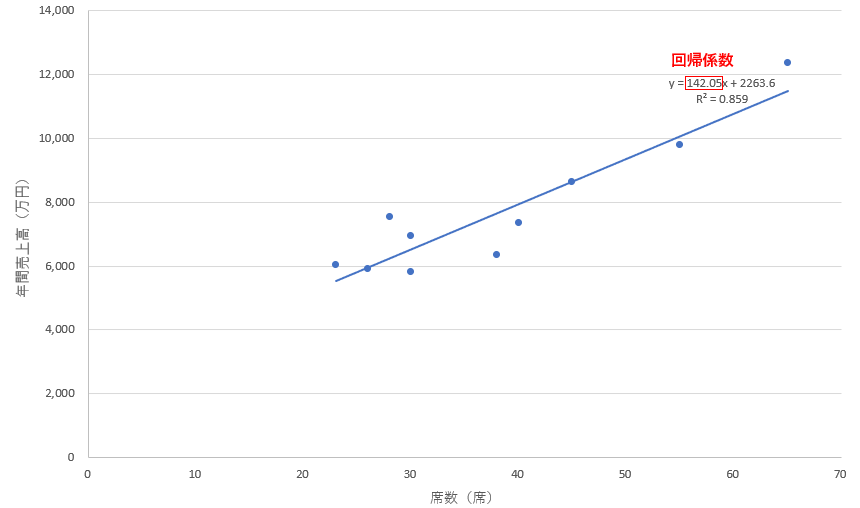

今回の例に当てはめると、この席数における回帰係数142.052…は「席数が1つ増えた場合に年間売上高が142.05万円増加する」ということを意味します。

ちなみに重回帰分析の回帰係数は偏回帰係数とも呼びます。「偏」の意味としては、他の説明変数の影響を除外した場合のその変数の重み、という意味です。
3-1-2.切片
回帰式の切片は説明変数の値が0の時の目的変数の値を表します。今回の例の場合は下図の 「2,263.6」 が切片に該当します。
●散布図の「近似曲線の追加」機能での回帰分析の表示
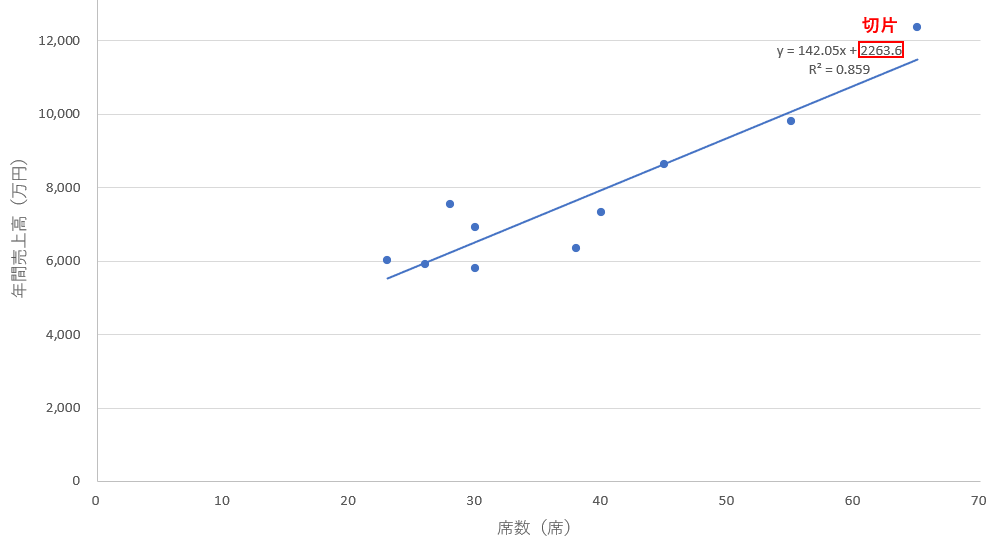
●分析ツールの「回帰分析」での表示

切片は説明変数が0の場合の目的変数の値を表しますが、あくまで各データに最もフィットする回帰式を求めた結果、推定された切片の値です。「席数が0の場合に年間売上高が2,263.6万円見込める。」と解釈するのは誤りなので注意しましょう。

3-2.R2乗(決定係数)
R2乗は「決定係数」や「寄与率」と呼ばれ、回帰分析の結果得られた回帰式が目的変数の値変動をどの程度説明できているかを表す指標です。R2乗は0〜1の値を取ります。R2乗が1に近ければ近いほど、データに対する当てはまりが良く、回帰式の精度が高いことを意味しています。なぜ、R2乗を確認する必要があるかというと、精度の悪い回帰式をその後の分析に用いるのを防ぐためです。
下図は単回帰分析において、R2乗の値が0.9と0.2の場合の回帰直線のデータの当てはまり具合を示したものです。
R2乗が1に近い0.9の方がデータに対する当てはまりが良いことがわかります。
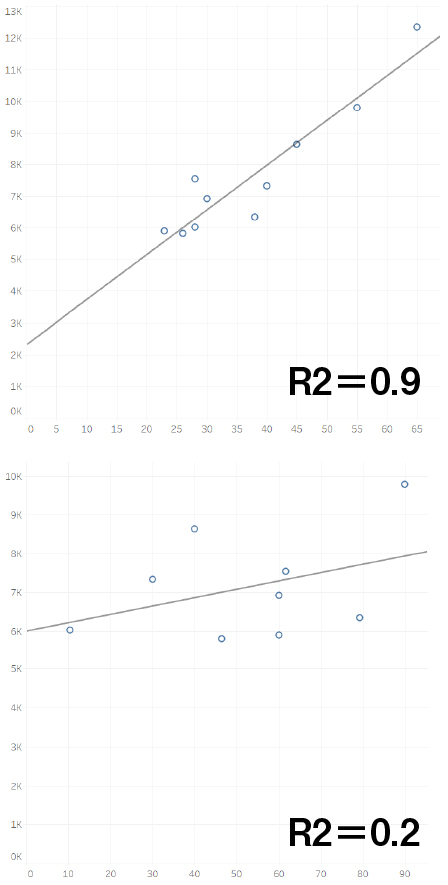
今回の例におけるR2乗は下記の通りです。
●散布図の「近似曲線の追加」機能での回帰分析の表示
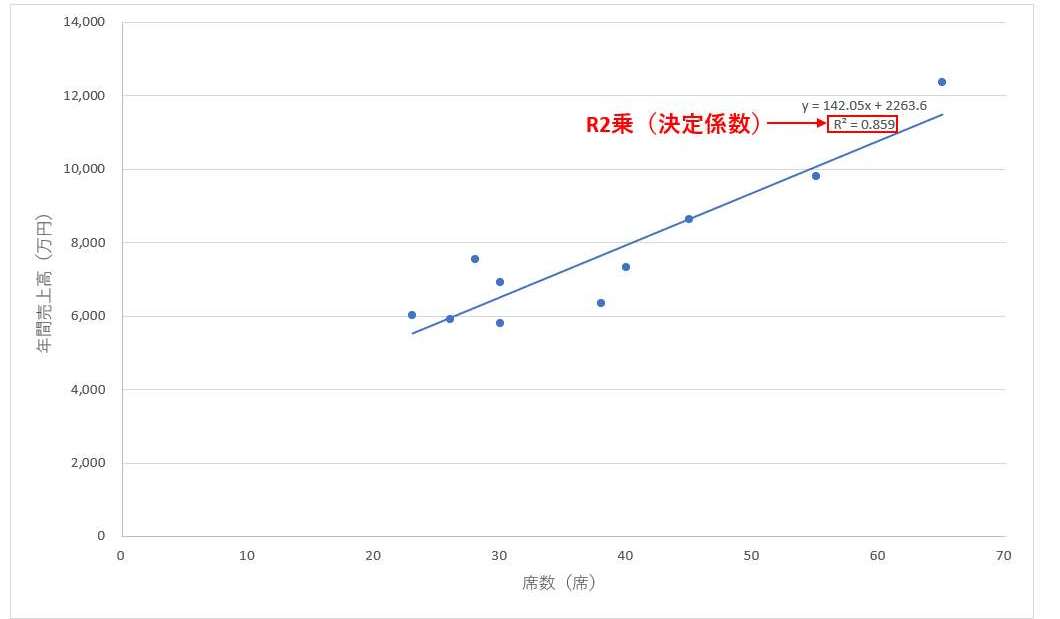
Excelの分析ツールで回帰分析を行う場合は下記の重決定R2がR2乗(決定係数)を表していますので、こちらを確認しましょう。
●分析ツールの「回帰分析」での表示
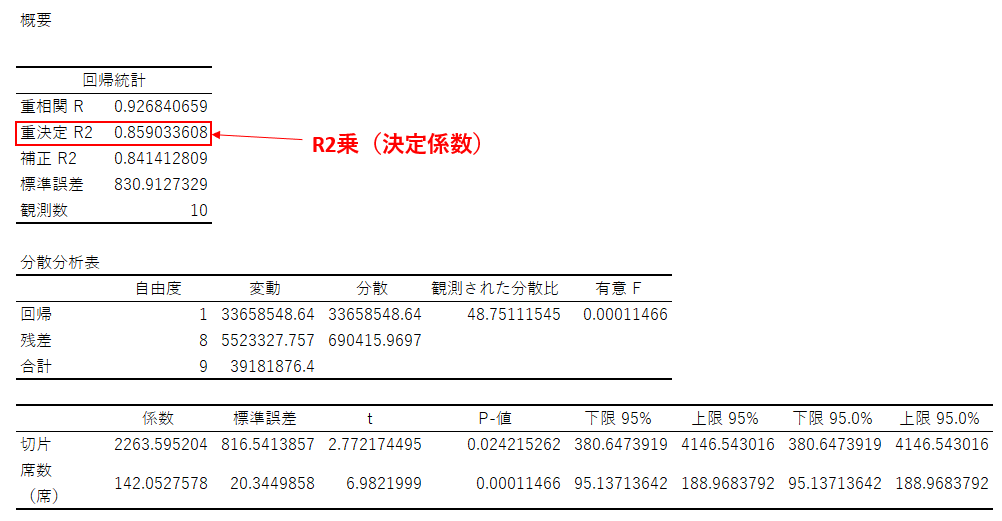
今回の例を確認するとR2乗が0.859となっています。これは「目的変数である年間売上高の値変動を説明変数である席数である程度精度高く説明できている」ということを意味しています。
重回帰分析の場合は補正R2の値を見る
単回帰分析の場合は説明変数が1つなので、R2乗(決定係数)の値を確認するだけで問題ありませんが、複数の説明変数を使って行う重回帰分析の場合は補正R2の値を確認しましょう。
※重回帰分析はExcelにおける散布図の「近似曲線の追加」機能で行うことはできません。
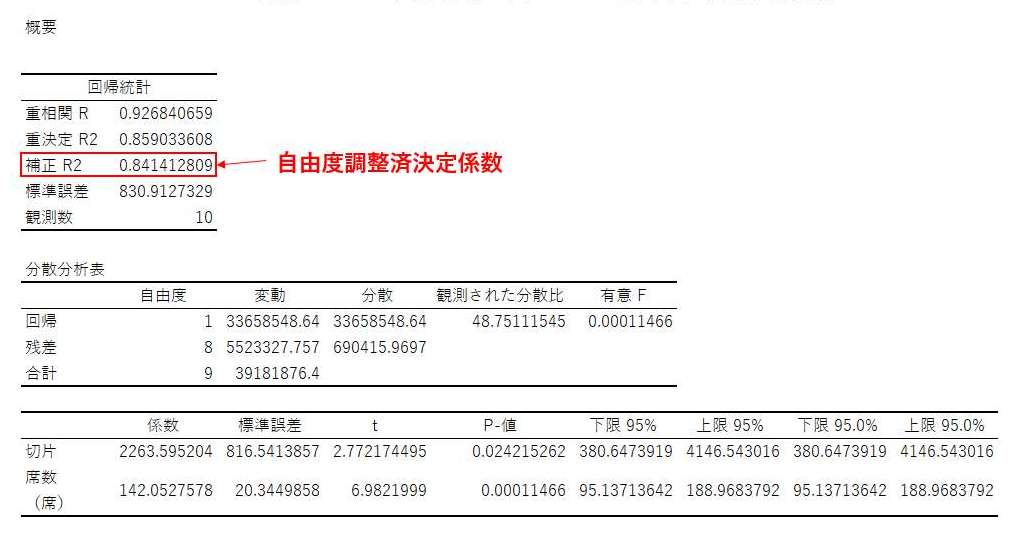
補正R2と表示されている欄は正しくは自由度調整済決定係数と呼ばれます。前述したR2乗(決定係数)は説明変数の個数が多くなればなるほど1に近づく性質があるため、重回帰分析の回帰式の精度を見るには限界があります。そのため、重回帰分析の場合は説明変数の個数の影響を取り除いた指標として補正R2(自由度調整済決定係数)の値を確認する必要があります。
3-3.有意F
有意Fは「回帰分析に使用した説明変数の組み合わせに意味はない」という確率を表すものです。この数値が小さければ小さいほど、「偶然の可能性が低い」=「意味のある回帰式を得られた」ということになります。
※有意FやP値、t値などはExcelの散布図の近似曲線の追加機能を使った回帰分析では表示されませんので、ここからはExcel分析ツールに絞って話を進めます。
一般的に有意Fが0.05未満であれば、有用な回帰式を得られたと判断できますが、実際にはこの水準は自身で定めることができ、ほとんどの場合、0.05もしくは0.01を設定します。
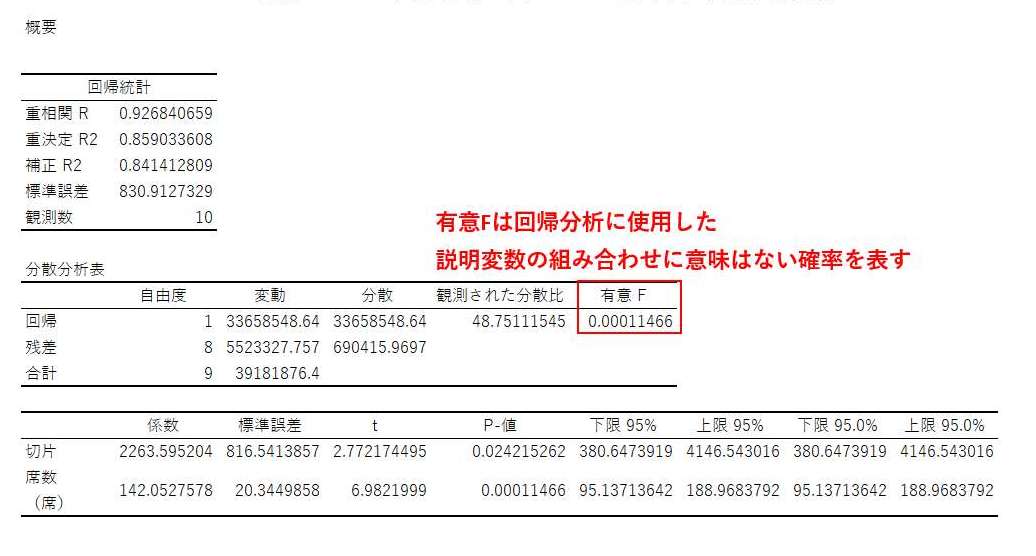
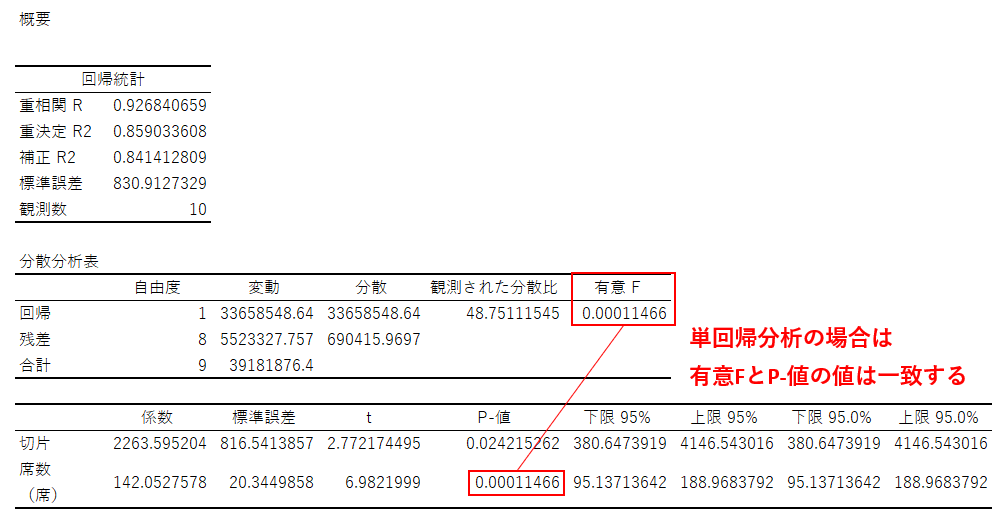
今回の例では有意Fが0.0001と0.01を大幅に下回っていますので、「回帰分析に使用した説明変数の組み合わせに意味がない確率は1%以下である」ということになるので、有用な回帰式が得られたとわかります。単回帰分析においては有意Fの値は後述するP値が一致しますので、P値を確認するのみで問題ありません。重回帰分析の場合は有意Fの値が定めた水準以下であるかを確認しましょう。
3-3.P値
P値は個別の説明変数1つ1つが目的変数に対して関係があるかどうかを表す指標です。Pは「provability(確率)」の頭文字です。
一般的にP-値が0.05未満であれば、その説明変数は目的変数に対して「関係性がある」という判断をします。0.05以上の場合は「関係がない」と捉えることができます。

有意Fが目的変数を説明するための説明変数の組み合わせに意味があるかどうかを表す指標に対し、P値は個別の説明変数が目的変数に対して関係があるかどうかを表します。説明変数のP値の大小は次に説明するt値と裏返しの関係にあり、P値が小さければ小さいほどt値は大きくなります。
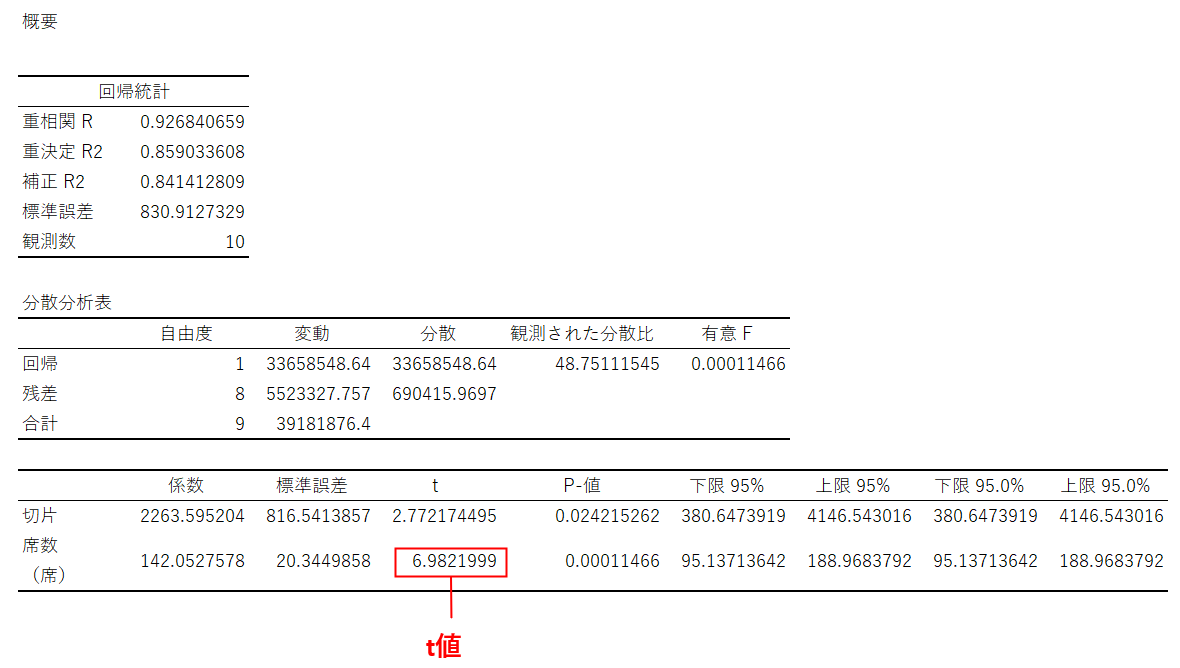
3-4. t値
t値はそれぞれの説明変数が目的変数に与える影響の大きさを表す指標です。t値の絶対値が大きければ大きいほど、目的変数に与える影響が強いことを意味しています。目安としてt値の絶対値が2より小さい場合は、統計的にその説明変数は目的変数に影響を与えていないと判断します。
4.Excelで行う回帰分析のステップ
それでは実際にExcelを使って、回帰分析を実施していきましょう。回帰分析は様々なツールで行うことが出来ますが、今回は多くの方が使用しているExcelで基本的な単回帰分析を行ってみます。
前述の通り、Excelで単回帰分析を行うには下記2通りの方法があります。
- 散布図を作成し、「近似曲線の追加」機能で回帰式を表示させる方法
- 分析ツールの「回帰分析」の機能を使う方法
1に関しては単回帰分析のみしか行えませんが、2の分析ツールを使う方法であれば重回帰分析も簡単に行うことが出来ます。いずれ重回帰分析まで行いたい方はぜひ2の分析ツールを使った回帰分析の実施方法を覚えてみてください。
4-1.散布図を作成し、「近似曲線の追加」機能で回帰式を表示させる方法
では、散布図の「近似曲線の追加」機能を使って回帰分析を行っていきます。この方法で行える回帰分析は説明変数が1つのみの単回帰分析のみとなります。
4-1-1.ステップ1 :分析に使うデータを用意する
まず分析に使うデータを用意します。今回は先程使用したデータと同じデータを使い、目的変数を年間売上高とし、説明変数は席数とします。

4-1-2.ステップ2:散布図を描く
次にExcelのグラフ機能を活用して2つの変数の関係を表す散布図を描きます。
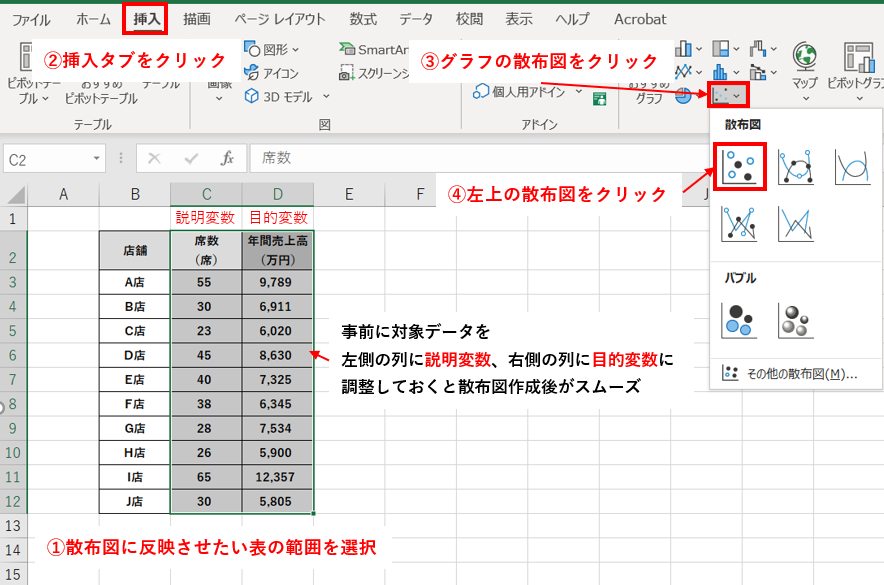
回帰分析を行うために散布図を描く時のポイントは目的変数を縦軸に、説明変数を横軸に入れることです。Excelでは選択した範囲の右側の列データが散布図の縦軸に、左側の列データが横軸になる仕様になっているため、上図のように説明変数の列を左側に、目的変数の列を右側にした状態にしておくと下図のように散布図が表示されます。
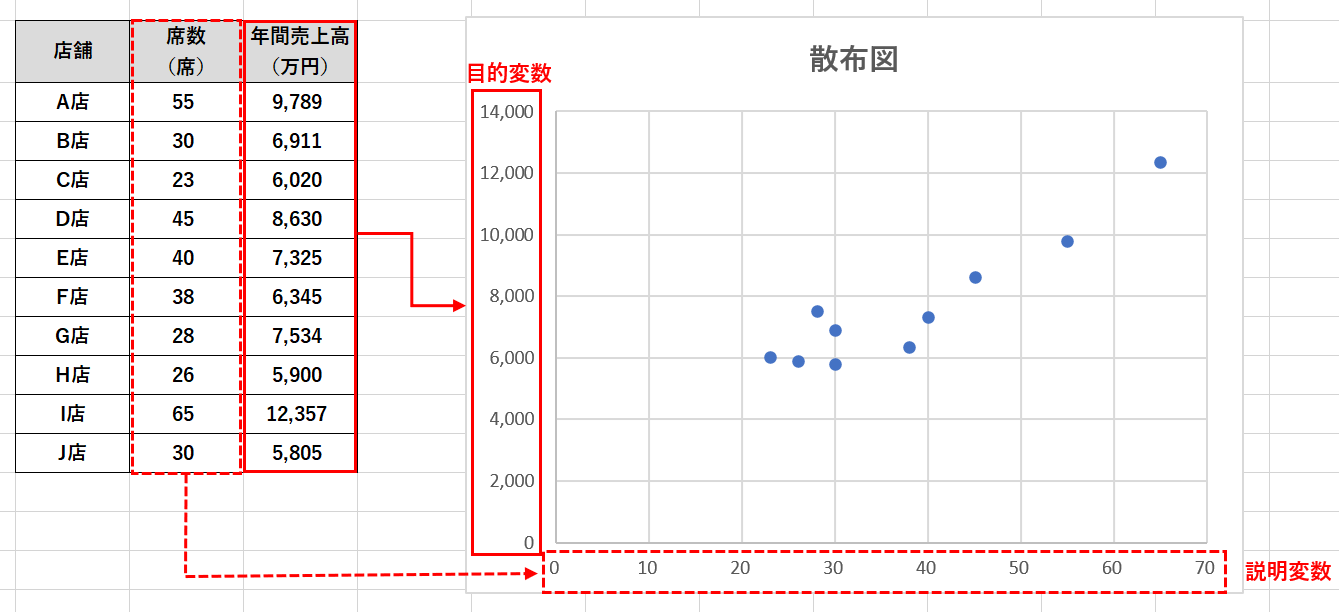
散布図が表示されましたが、下記を行うと散布図が見やすくなり、回帰分析が行いやすくなります。
- プロットエリア(データの点が表示されているエリア)を正方形
- 縦軸と横軸の軸ラベルを表示し、軸の項目名を入力
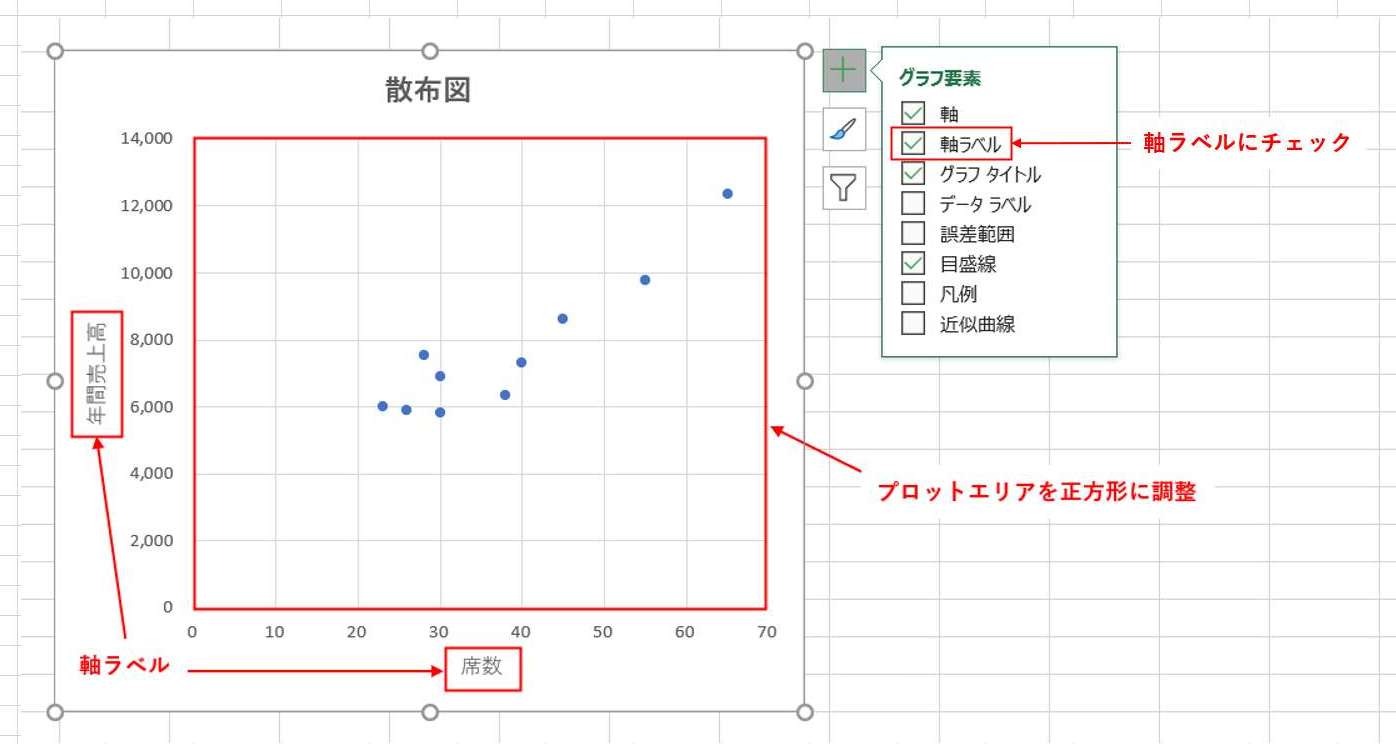
4-1-3.ステップ3:近似曲線を追加する
散布図が作成できたら、「近似曲線の追加」機能を使って、データにフィットする回帰直線を引いていきます。
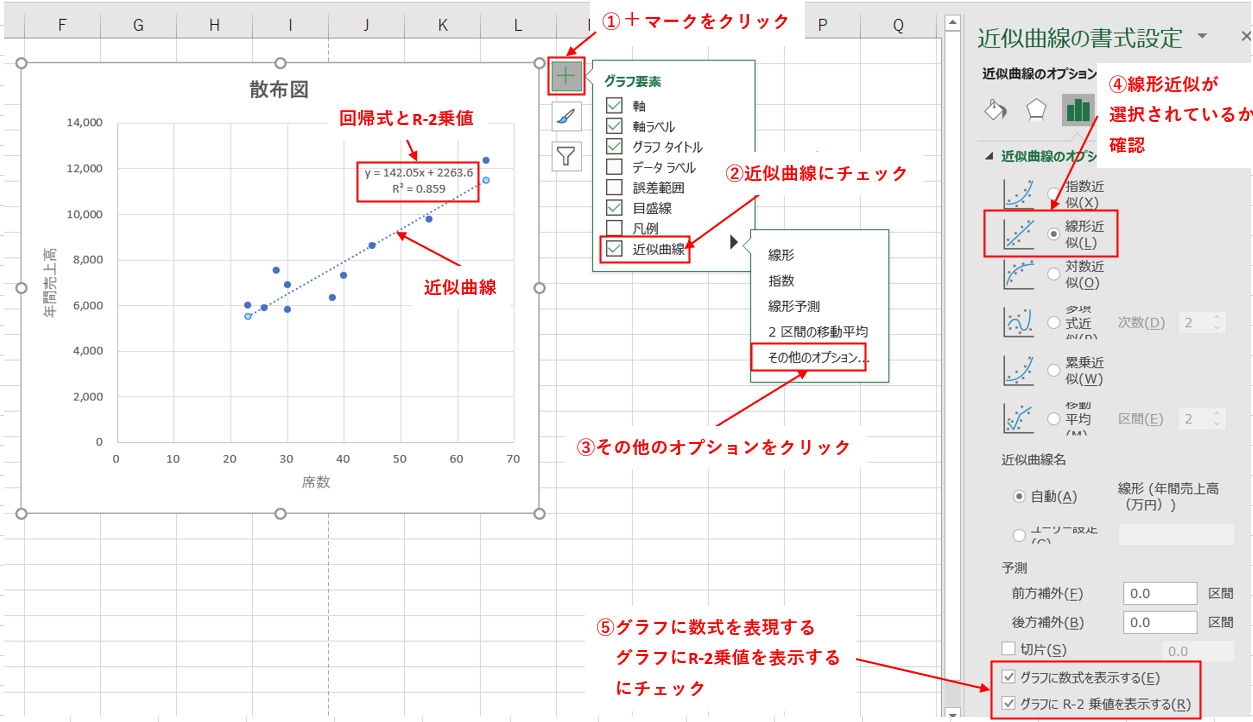
散布図に近似曲線を追加するだけだとグラフに回帰式やR-2乗値が表示されませんので、上図の⑤のように下記にチェックを入れて表示させるようにしましょう。
- グラフに数式を表示する(回帰式を表示するため)
- グラフにR-2乗値を表示する(R2=決定係数を表示するため)
4-1-4.ステップ4:回帰式の妥当性を評価する
回帰式とR2乗が表示されたら、回帰式の妥当性を評価しましょう。散布図の「近似曲線の追加」機能で表示される回帰式は下記のように目的変数がy、説明変数がxで表されています。
- y=142.05x+2263.6
このままだと他の人に説明する時もわかりにくいので、実務においては下記のように直感的に式の意味が理解できるように表示の仕方を工夫するのがおすすめです。
- 年間売上高(万円)=142.05×席数(席)+2263.6(万円)
この回帰式のR-2乗値は0.859でしたので、「比較的精度の高い回帰式を得られた」という評価をすることが出来ます。
本来であれば、これに加えてP値やt値を確認して、より詳細に回帰式の妥当性を評価したいところですが、Excelの散布図の「近似曲線の追加」機能による回帰分析ではt値やP値は確認することが出来ません。分析ツールでの回帰分析を行うか、関数を使って別途求める必要があります。
そのため、回帰分析をExcelで本格的に行いたい場合は重回帰分析も行うことが出来る分析ツールでの「回帰分析」を行うのをおすすめします。
4-2.分析ツールの「回帰分析」の機能を使う方法
次にExcel分析ツールでの「回帰分析」の機能を使う場合のステップを確認しましょう。
4-2-1.ステップ1: Excelの分析ツール機能を導入する
まず分析ツールを活用できる状態にする必要があります。そもそも分析ツールとはExcelのアドインの1つで、クリックや簡単なパラメータ入力のみで様々なデータ分析を可能にする機能です。
Windowsにおける分析ツールの導入方法は下図です。WindowsとMacでは導入方法が若干異なるので、Macの方はこちらで導入方法を参照してみてください。
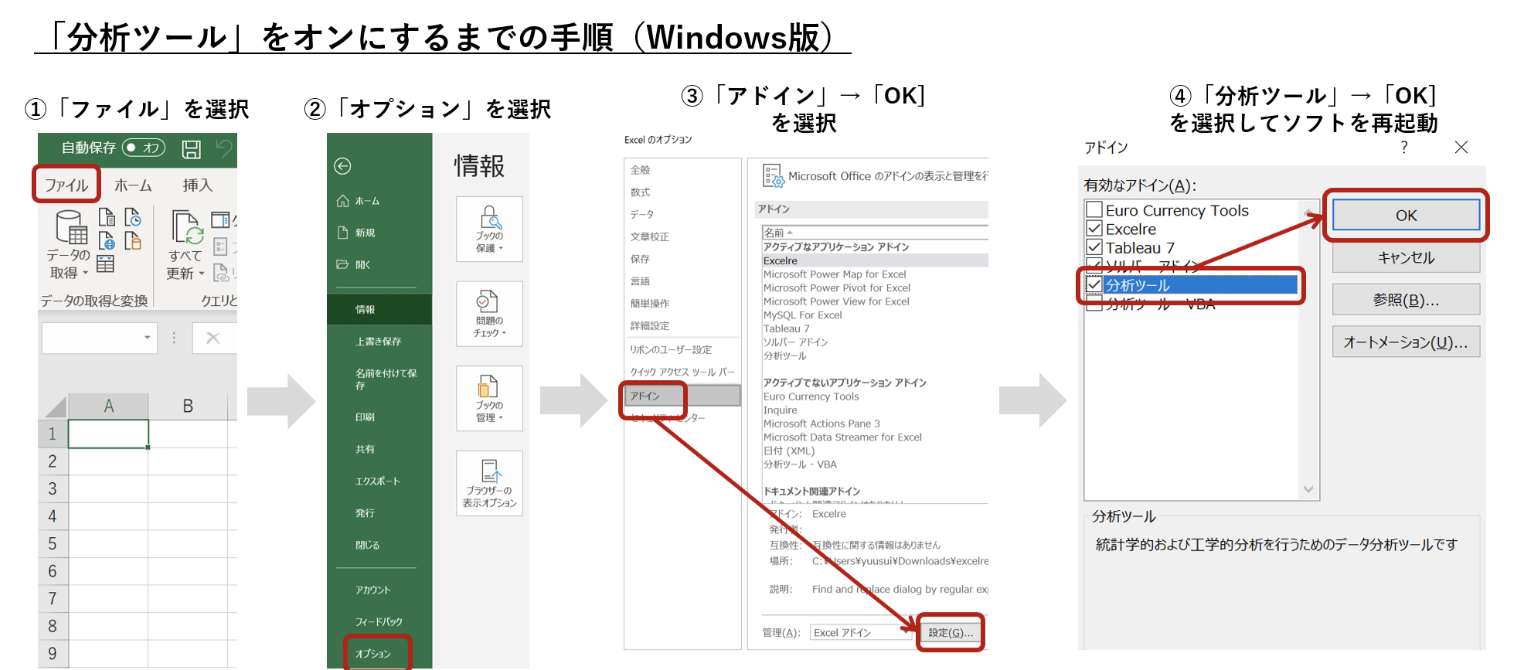
【導入手順(Windows版)】
- Excelを開いた画面から「ファイル」を選択
- 左端のバーから「オプション」を選択
- 新しく開いたウィンドウで、「アドイン」→「設定」を選択
- さらに開いたウィンドウで、「分析ツール」にチェックを付け「OK」をクリック、ソフトを一度閉じ再び開く
問題なく上記手順が行えれば下記のようにデータタブ内に「データ分析」が表示されるようになります。
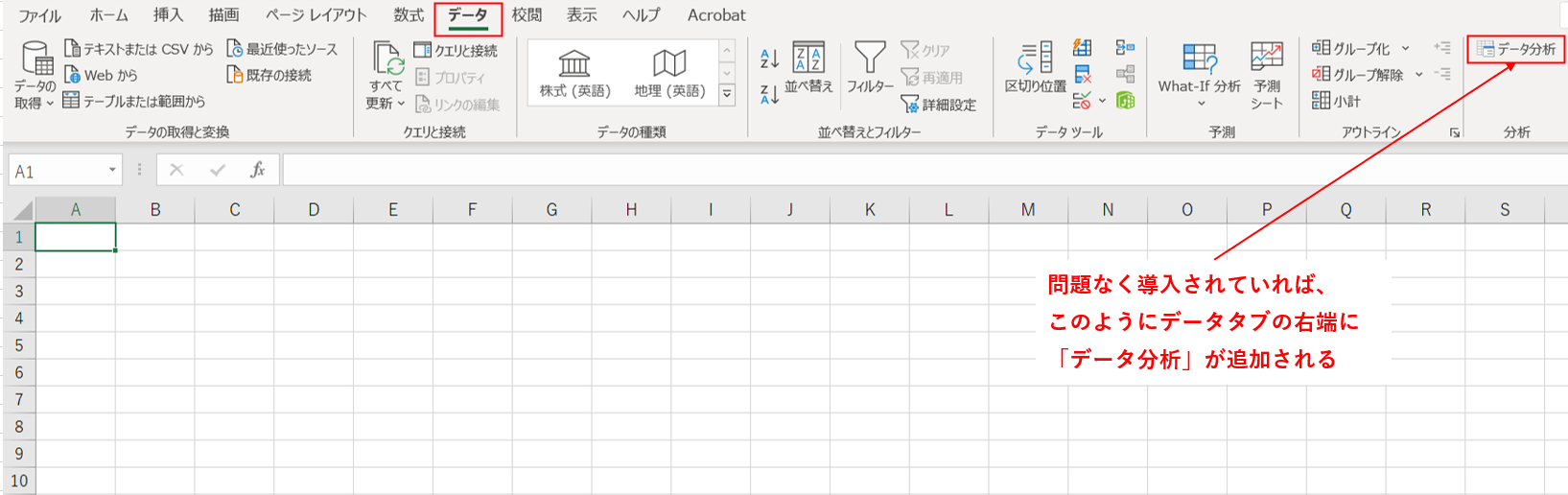
4-2-2.ステップ2 :分析データを用意する
次に散布図の「近似曲線の追加」機能と同様に分析データを用意します。今回は4-1-1と全く同じデータを使用して回帰分析を行います。
4-2-3.ステップ3 :分析ツールで回帰分析を行う
データが用意出来たら、分析ツールで回帰分析を行っていきます。手順は下図の通りです。
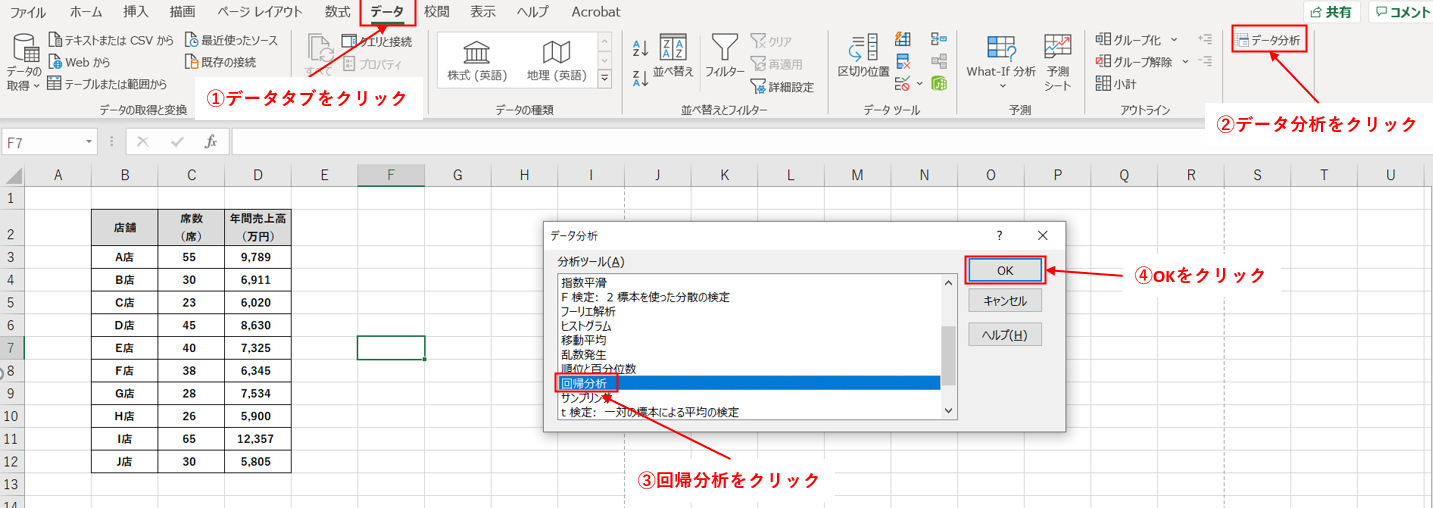
データ分析ツールより回帰分析を選択した結果、次に表示されるダイアログで下図のように設定を行います。
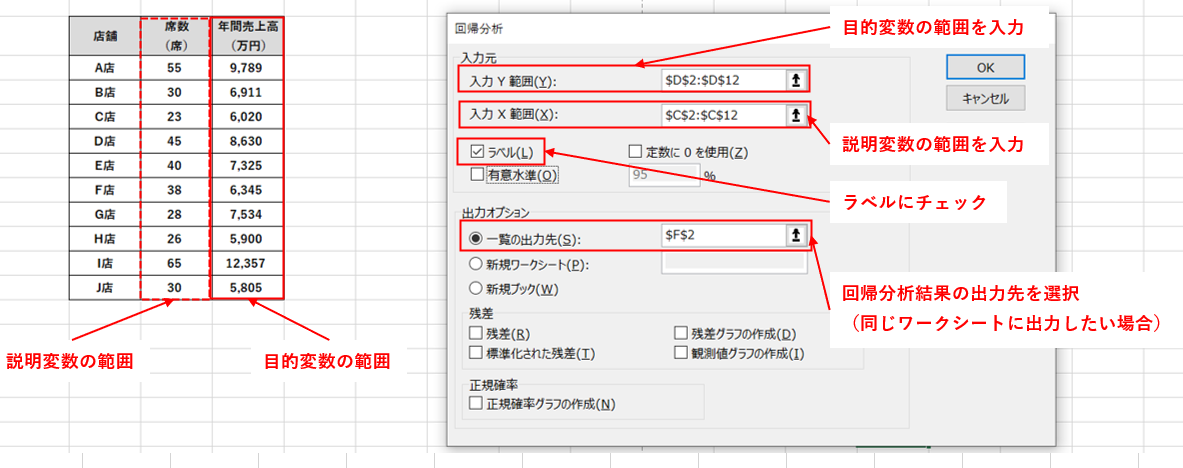
- 入力Y範囲:目的変数(年間売上高のデータ)の範囲を指定
- 入力X範囲:説明変数(席数)の範囲を指定
- ラベル:上で指定した範囲にデータ名(年間売上高や席数、というデータ名)を含めたい場合はチェック
※ラベルにチェックを入れない場合は、入力Y・Xの範囲からデータ名のセルを外す - 出力オプション:分析結果を同じワークシート上に表示させたい場合は一覧の出力先に表示させたい場所のセルを入力
一通り入力して、ダイアログの「OK」をクリックすると、下記のように結果が出力されます。
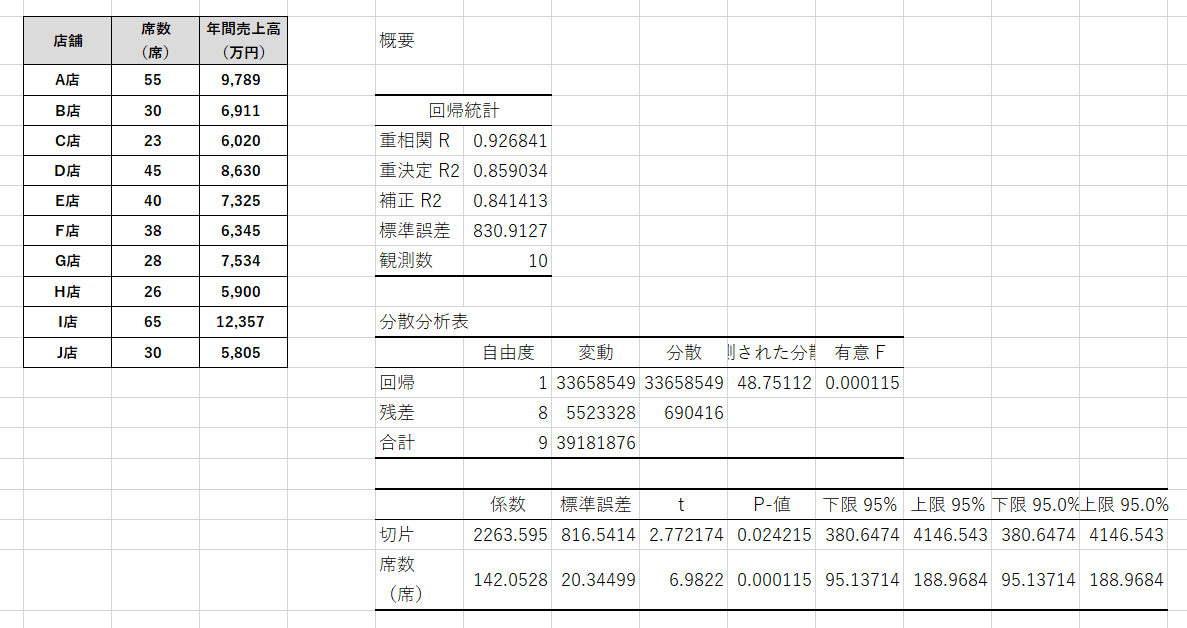
4-2-4.ステップ4 分析結果を解釈する
次にステップ3で表示された回帰分析の結果を解釈します。解釈をするために見るべき指標は3章で紹介しましたが、それらの指標を下記の流れで確認するといいでしょう。
回帰式を確認する
分析ツールで回帰分析を行うと散布図の「近似曲線の追加」機能の際と異なり、下記のような回帰式が表示されません。
- y=142.05x+2263.6
その代わり、回帰式を作るための情報は表示されていますので、それを基に回帰式を作って確認しましょう。
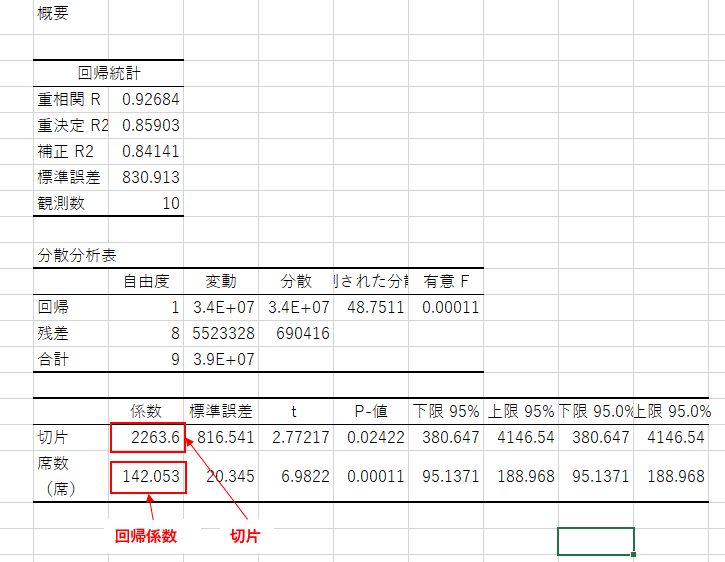
得られた情報から下記の回帰式を作ることが出来ます。
- 年間売上高(万円)=142.05×席数(席)+2263.6(万円)
同じデータを使用しているので当たり前ですが、散布図の近似曲線の追加機能と全く回帰式になっていますよね?分析ツールを使う場合は回帰式に必要な情報が上図のように表示されていることを覚えておいてください。
推定された回帰式の精度をみる
3章でも確認しましたが、回帰式の精度をみるためには決定係数である重決定R2を確認します。

※重回帰分析の場合は補正R2を確認しましょう。
説明変数1つ1つが目的変数に対して関係があるかどうかを確認する
次に「それぞれの説明変数が目的変数に対して関係があるかどうか?」をP値で確認します。前述の通り、P-値が0.05未満であれば、その説明変数は目的変数に対して「関係性がある」という判断をします。

説明変数である席数のP-値を見ると0.00011と0.05未満の値なので、「説明変数である席数は目的変数である年間売上高と関係がある」と判断できます。
※重回帰分析の場合はP値を確認する前に「目的変数を説明するための説明変数の組み合わせに意味があるかどうか?」を有意Fの値で判断しますが、単回帰分析の場合は有意FとP-値の値が一致するので不要です。
各説明変数の影響度を確認する
次にそれぞれの説明変数の影響度をt値で確認します。前述の通り、t値の絶対値が2より小さい場合は、統計的にその説明変数は目的変数に影響を与えていないと判断します。

4-2-5.ステップ5 回帰式を使って、実際に予測してみる
得られた回帰式が有用であると確認が出来たら、その回帰式に他のデータ(例えば新規出店する店舗の席数)を当てはめて、予測を行っていきましょう。
5.回帰分析に関するよくある質問
最後に回帰分析を学び始めたときに出てくるよくある質問に回答します。
5-1.回帰分析と相関分析の違いは?
回帰分析は「一方の変数がこれだけ増えると、他方の変数がどれだけ増えるか」と言うように、目的変数に対する説明変数の影響力の大きさを把握する分析手法である一方、相関分析は「一方の変数と他方の変数がどのように関係しているか?」を把握する分析手法です。
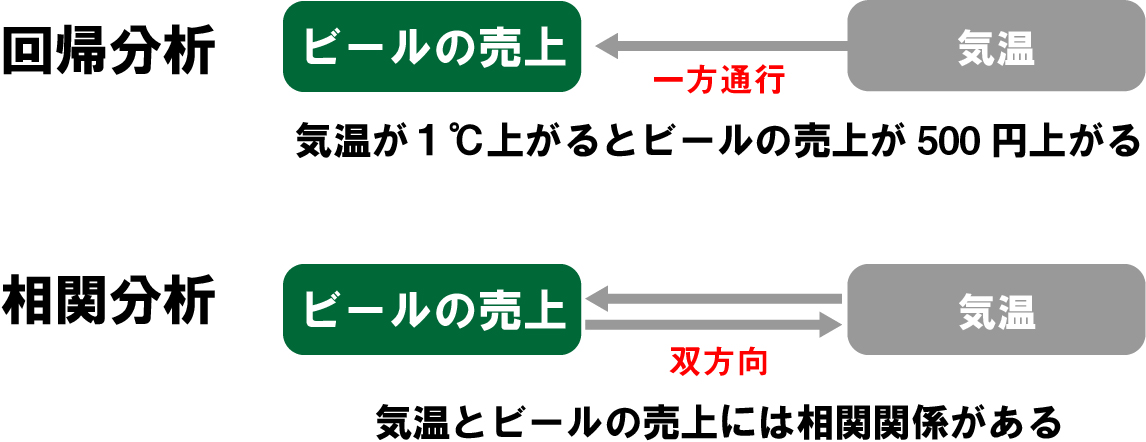
回帰分析の場合は、「目的変数の値変動を説明変数が説明する」という一方通行の関係であるのに対し、相関分析の場合は双方向の関係です。例えば、回帰分析の結果「気温が1℃上がるとビールの売上が500円増加する」と判明した場合、これは一方通行の関係で「ビールの売上が500円上がったら、気温が1℃上がる」という逆の関係は成立しません。
相関分析の結果、「気温とビールの売上には関係性がある」ということが分かった場合、「ビールの売上と気温には関係性がある」ということも可能です。相関分析では「ビールの売上と気温には関係性がある」ということまではわかりますが、「気温がビールの売上にどれくらい影響を与えているか?」を把握することまではできません。
相関分析についてはこちらの記事で詳しく解説しています。
5-2.重相関Rと重決定R2は何が違う?
Excel分析ツールで回帰分析を行った場合に表示される「重相関R」と「重決定R2」の違いは下記です。
(重相関R)²=重決定R2
つまり、重相関Rを二乗した値と重決定R2の値が一致します。
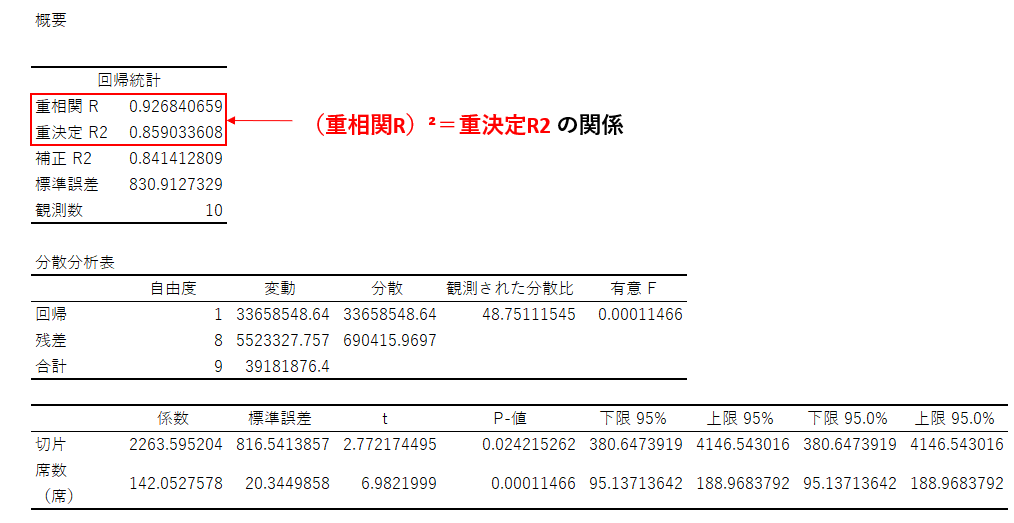
重相関Rとは正しくは重相関係数と呼ばれ、目的変数の元データと回帰式の推定値との相関係数の絶対値のことです。重決定R2と同様に0~1の値を取ります。
5-3.決定係数R2の目安は?
残念ながら決定係数R2がいくつ以上であれば良い、という統計学的基準はありません。そのため、決定係数R2の基準は、回帰分析を行う人が経験的な判断から決めることになります。
ただ、一般的な目安としては0.5や0.6以上あれば、有用な回帰式が得られたという判断をする場合が多いようです。
※あくまで目安になるので、状況に応じて異なります。
ただ、1つの目安としては私は下記のような基準で行っています。
- R2≧0.8 精度が良い
- R2≧0.5 精度がやや良い
- R2≧0.2 精度が悪い
上記はあくまで私の基準です。他のデータサイエンティストの方だとR2≦0.6だと全く使えない、という人もいますので、目安の1つ程度で把握していただければと思います。
5-4.ExcelとRとPythonの中で回帰分析ができるのはどれか?
Excel、R、Pythonのどのツールにおいても回帰分析を行うことが出来ます。
まとめ
回帰分析は、説明変数が目的変数に与える影響度合いを数値として表すもので、売上等の予測や要因分析に活用できる便利な手法です。本記事をきっかけに回帰分析を深く理解し、仕事で活用できるようになれば、今まで気づけなかった様々な示唆を得ることができるようになるはずです。
今回は初めての方向けの記事だったため、シンプルな単回帰分析を中心に説明しましたが、慣れてきたら実務でよく使われる重回帰分析を勉強してみてください。重回帰分析については下記記事で詳しく解説しておりますので、興味がある方はぜひお読みください。
また、データの管理・活用でお困りの場合はデータビズラボへお問い合わせください。
状況やニーズに合わせた様々なサポートをご提供いたします。





コメント