Excelを活用したデータ分析の方法

多くの人は、エクセルでのデータ分析はなかなか難しいと思っているかもしれません。しかし、専門の分析ツールを使わなくとも、できることは意外に多いんです。

エクセルには「分析ツール」という大変便利な機能があります。

「分析ツール」とはエクセルのアドインの一つで、クリックや簡単なパラメータの入力のみでデータ分析を可能にしてくれる機能です。

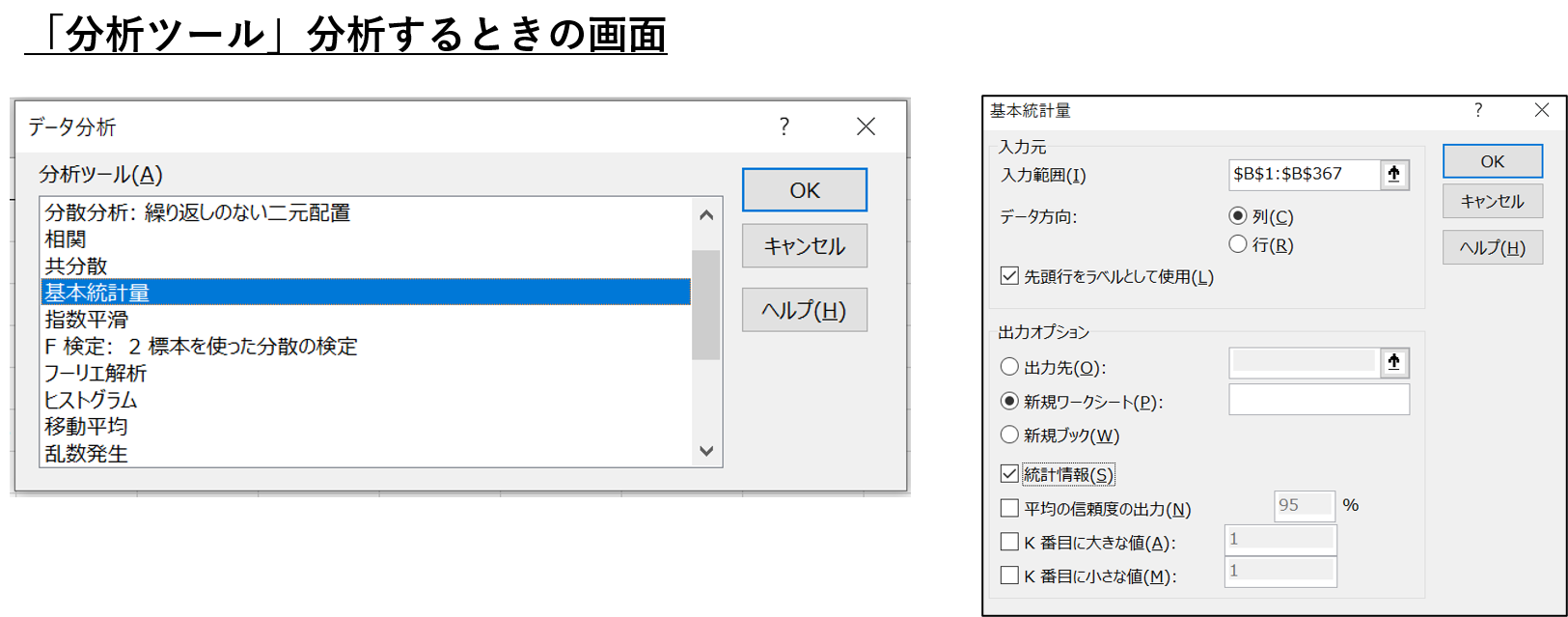
「分析ツール」機能を使用すれば、特別な関数やコードを書く必要が一切ありません。導入も簡単ですので、初心者でも気軽にデータ分析を行うことができます。

本記事では、エクセルにある「分析ツール」機能を使って、「エクセルのデータ分析でどこまでいけるのか」を8つのケースを通じて解説します。

この記事を読み終えたころには、「分析ツール」機能でデータ分析ができるようになっているはずです！

1. 「分析ツール」機能は、短い時間で少量のデータを分析したいときに最適な機能である

「データ分析は難しいうえに時間がかかりそう」と考えられている方も少なくないと思います。しかし「分析ツール」機能を用いれば様々な分析を、1つ約30秒ほどで分析できてしまいます。

この章では、「分析ツール」機能の概要や特徴に関して詳しく解説したいと思います。

「分析ツール」機能を使用すれば、30秒で分析ができる

「分析ツール」機能を使用したデータ分析は、マウスでポチポチするだけで行うことができます。具体的には、以下の3stepで分析を行います。

1. データを準備する
2. 「データ」→「データ分析」→行いたい分析手法→「OK」を選択
3. 必要な項目を選択して「OK」を選択

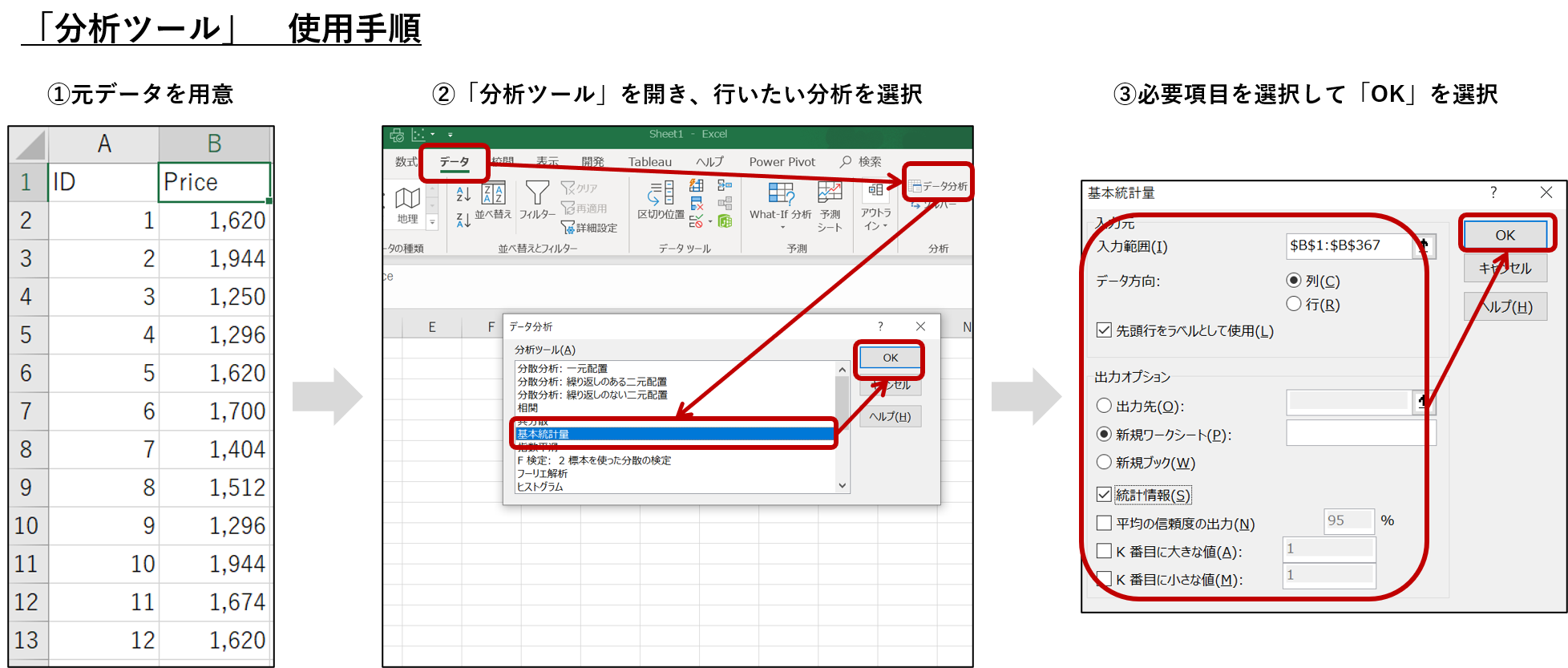
この3step以外の操作は基本的に必要ありません。

このように関数や追加列の作成などを行わずとも、かなり直感的な操作で簡単に分析することができます。

分析ツールで19種類もの分析ができる

この「分析ツール」機能は、ヒストグラムの作成から回帰分析まで19種類もの分析を可能にしてくれます。以下は「分析ツール」機能で行える分析です。

相関分析から統計的検定、回帰分析までサポートされているので、分析手法の基本どころは「分析ツール」でカバーできます。

以下は弊社が過去に開催したExcel分析ツールに関するセミナー動画です。概要から実用性の高い分析手法まで紹介しておりますので、是非ご視聴ください。

一番嬉しいポイントは、関連指標を複数同時に計算してくれ、表やグラフにもしてくれる

簡単な操作だけでデータ分析ができることは「分析ツール」機能の一つの特徴です。

ただ筆者が実際に分析を行っていて最も感銘を受けた点は、出力される値が一つだけではなく、その分析に関係する複数の指標を表やグラフの形式で出力してくれたことです。

以下は、「分析ツール」機能を利用して回帰分析と移動平均の分析を行ったときの出力です。

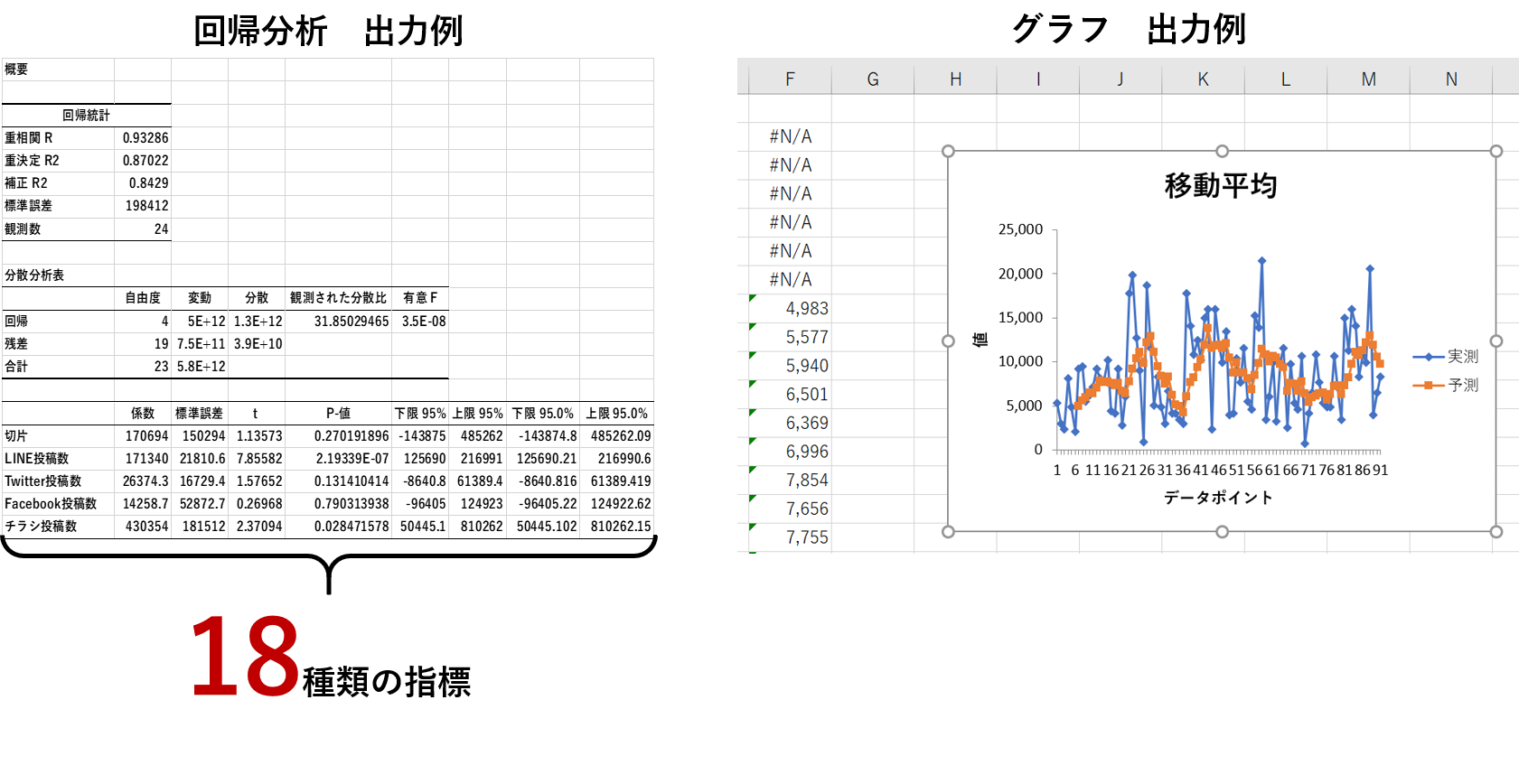
たった3step・30秒で18種類の指標やグラフを出すことができます。

表やグラフの形にレイアウトを整える部分に時間がかかる場合もあるので、このようにすべて整えて出力されるのは大幅な時短につながります。

DXのお悩みを解決する「DXの羅針盤」をダウンロードする

2. 「分析ツール」機能にも3つの欠点がある

「分析ツール」機能は大変便利な機能ですが、大きく3つの欠点があります。この欠点を抑えておくことで、効果的に「分析ツール」機能を使用できるようになります。

本章では、「分析ツール」機能の持つ3つの欠点について解説していきます。

➀ あらかじめ設定されていない分析は行えない

「分析ツール」機能には19種類の分析手法が用意されていることは先ほど紹介いたしました。当たり前ですが、「分析ツール」機能ではこれ以外の分析手法はサポートもされていなければ、カスタムで追加することもできません。

例えば因子分析や主成分分析は「分析ツール」機能で扱うことができません。

もしサポートされていない分析を「分析ツール」機能のような手軽さで行いたい場合は、エクセルVBAというプログラミング言語を利用するか、ほかのツールを使用する必要があります。

② 数十万行あるデータに使用するとエクセルがフリーズする

データの容量が大きくなると、「分析ツール」では処理できなくなります。

実際に私のPC（メモリは8GB）を用いて、たった1列しかないデータで「分析ツール」機能を試したところ、15万行までは処理できましたが、20万行になるとエクセルが応答しなくなりました。

もともとエクセルには約100万行までしかデータを格納することができず、数十万行のデータに関数を使用したりするとパフォーマンスが落ちます。

このように、分析したいデータの容量には気を付ける必要があります。

➂ 一度行った作業が残らず、2回目も同じ作業をする必要がある

「分析ツール」機能を使わず、関数を使用して指標の計算をしている場合、参照元のデータを入れ替えてあげるだけで指標も自動で再計算されます。しかし「分析ツール」機能を使用した場合、自動で出力結果が更新されないため、再度「分析ツール」機能を開いて計算する必要があります。

短期間でデータが更新され、そのデータを逐一分析したい場合、「分析ツール」機能に依存していると毎回同じ作業を一から行う必要が出てきます。

以上のように「分析ツール」機能にもその価値を発揮できないシーンがあります。そのため、以下が「分析ツール」を効果的に使用するときの3条件になります。

これらの条件をクリアしたら、それは分析ツールの使い所、とも言えます。それでは早速、「分析ツール」機能を導入して分析を行ってみたいと思います！

3. 「分析ツール」機能を30秒で導入する

エクセルの「分析ツール」機能は初期設定ではオフになっているため、使用できる状態に設定してあげる必要があります。ただし特にダウンロードもしないので、とても簡単に導入して使用することができます。

本稿ではWindows版の導入方法を解説していきます。WindowsとMacでは導入方法が若干異なるので、Macの方はこちらで導入方法を参照してみてください。（キャプチャではExcel2016を使用したものを掲載しています。）

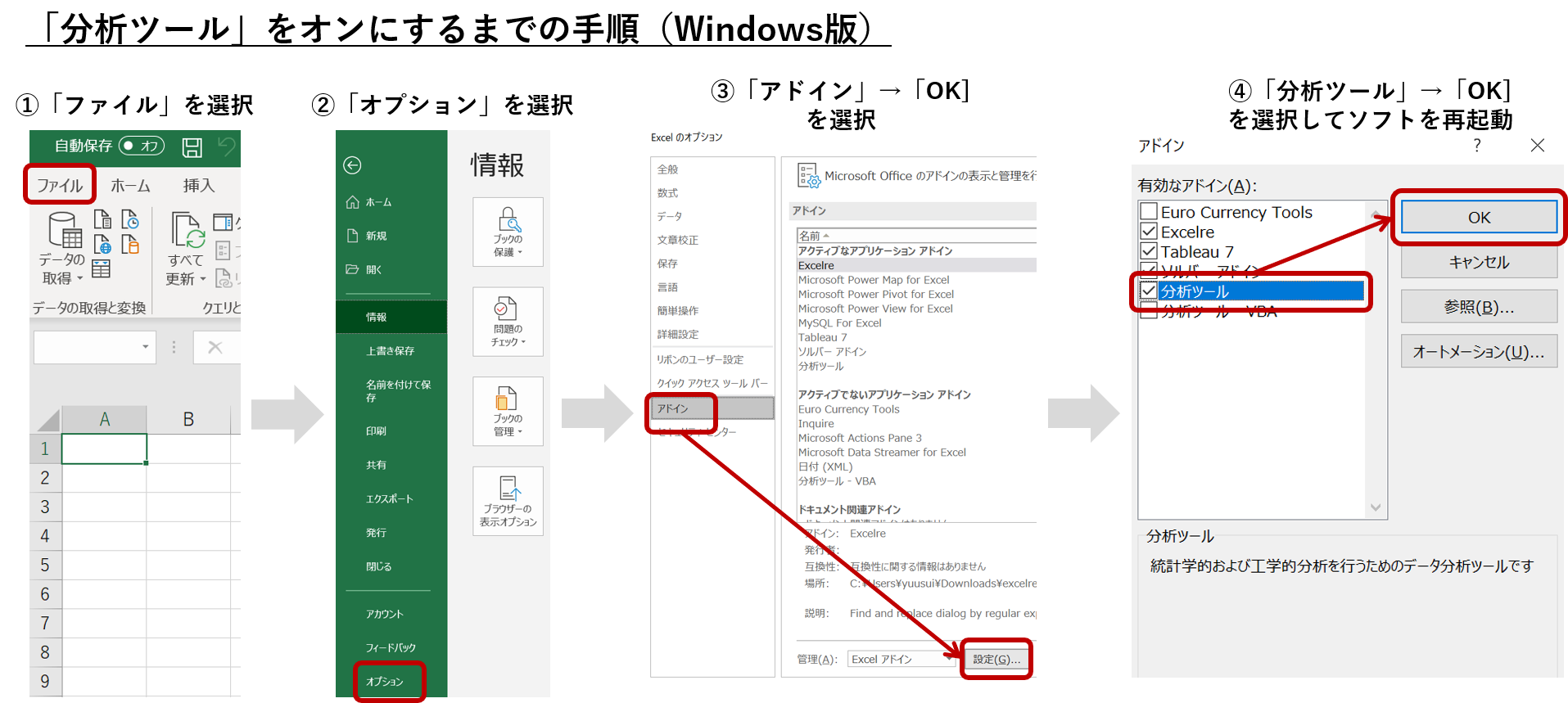
【導入手順（Windows版】

1. エクセルを開いた画面から「ファイル」を選択
2. 左端のバーから「オプション」を選択
3. 新しく開いたウィンドウで、「アドイン」→「設定」を選択
4. さらに開いたウィンドウで、「分析ツール」にチェックを付け「OK」を選択。ソフトを一度閉じ再び開く

4. さっそく「分析ツール」機能を使ってみよう！8つのケースを解説

分析ツールが導入できたら、さっそく架空のカフェのデータを利用して分析を行ってみたいと思います。今回の分析では、実務でよく見かける分析手法を用いて8つのケースを分析してみたいと思います。

全ての操作のキャプチャを掲載しているので、手元にあるデータですぐに実践できると思います。

また初めて聞くような分析手法があるかもしれませんが、各手法に関して解説もしていますので、どのケースに対しても気軽に取り組むことができます。

ケース①：基本統計量でデータの全体像をつかむ

使用する手法：基本統計量

基本統計量でデータの全体像を把握することからデータ分析は始まります。

データ分析の定石は「大まかな指標から細かい指標を見ていく」です。データに関するすべての事項を見ていたらきりがないため、おおざっぱにデータを眺めてから、絞り込むように深堀りをしていきます。

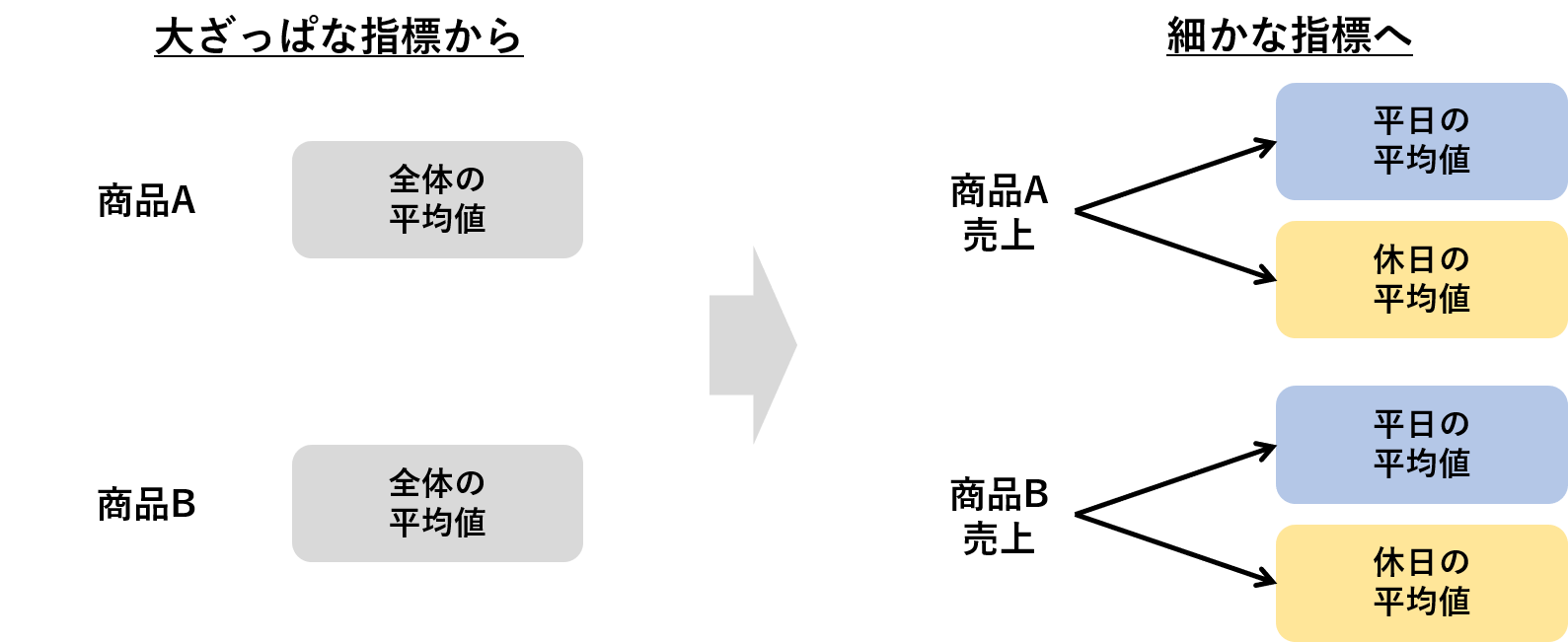
この「大まかな指標」の出発点は、平均値や中央値など基本統計量と呼ばれるものにあたります。この基本統計量から分析したいデータの基礎的な情報を得てから、データ分析を行うのが一般的です。

基本統計量とは

基本統計量とは、データの特徴・性質をあらわす代表的な値で、代表値、要約統計量とも呼ばれたりします。

エクセルの「分析ツール」機能では、以下の基本統計量を一括で出力することができます。

分析を行う

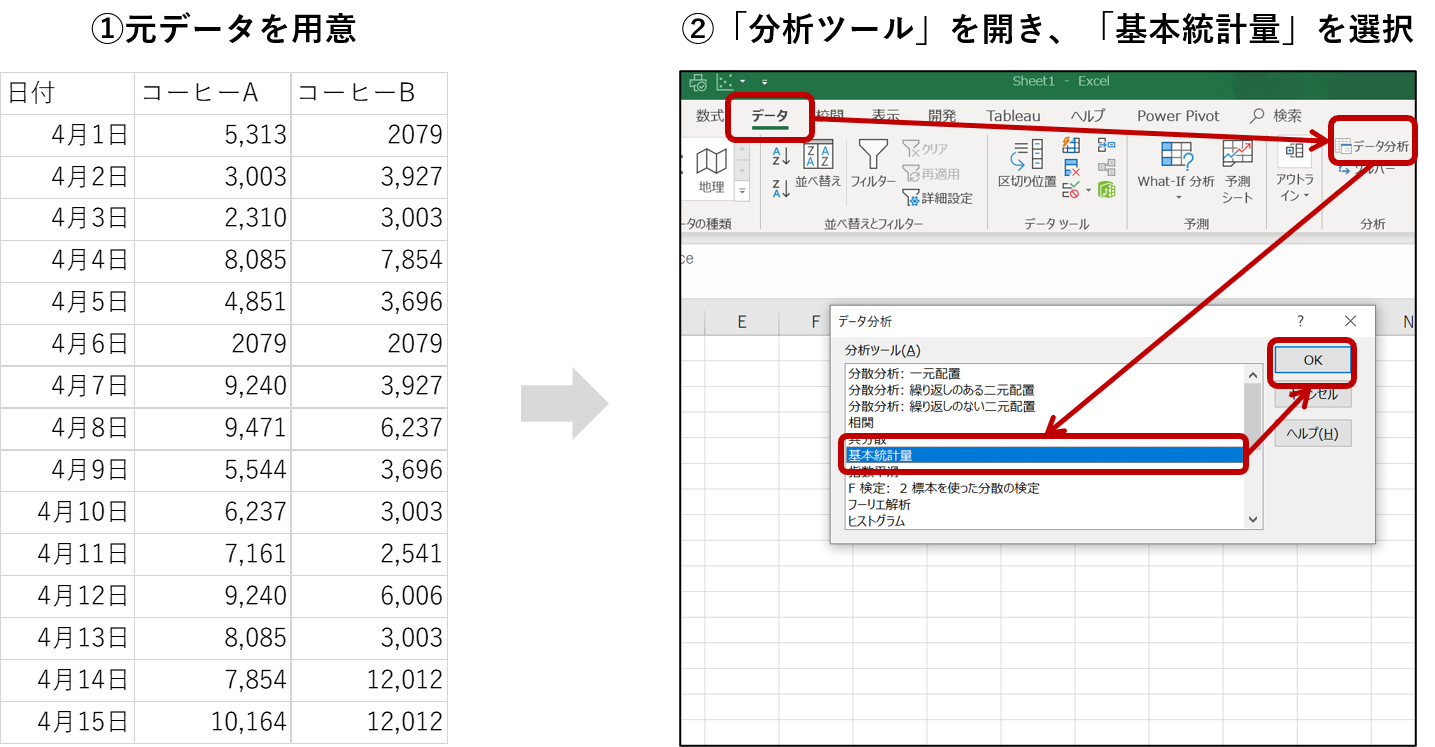
それでは基本統計量を求めてみます。今回は2つの商品の日別売上に関する基本統計量を見てみます。

まず、データを用意して、「分析ツール」を開き、「基本統計量」を選択します。

「入力範囲」で分析するデータを指定し、以下のように設定して「OK」を選択すると結果が出力されます。（出力結果は見やすいように最小限の編集をしています）

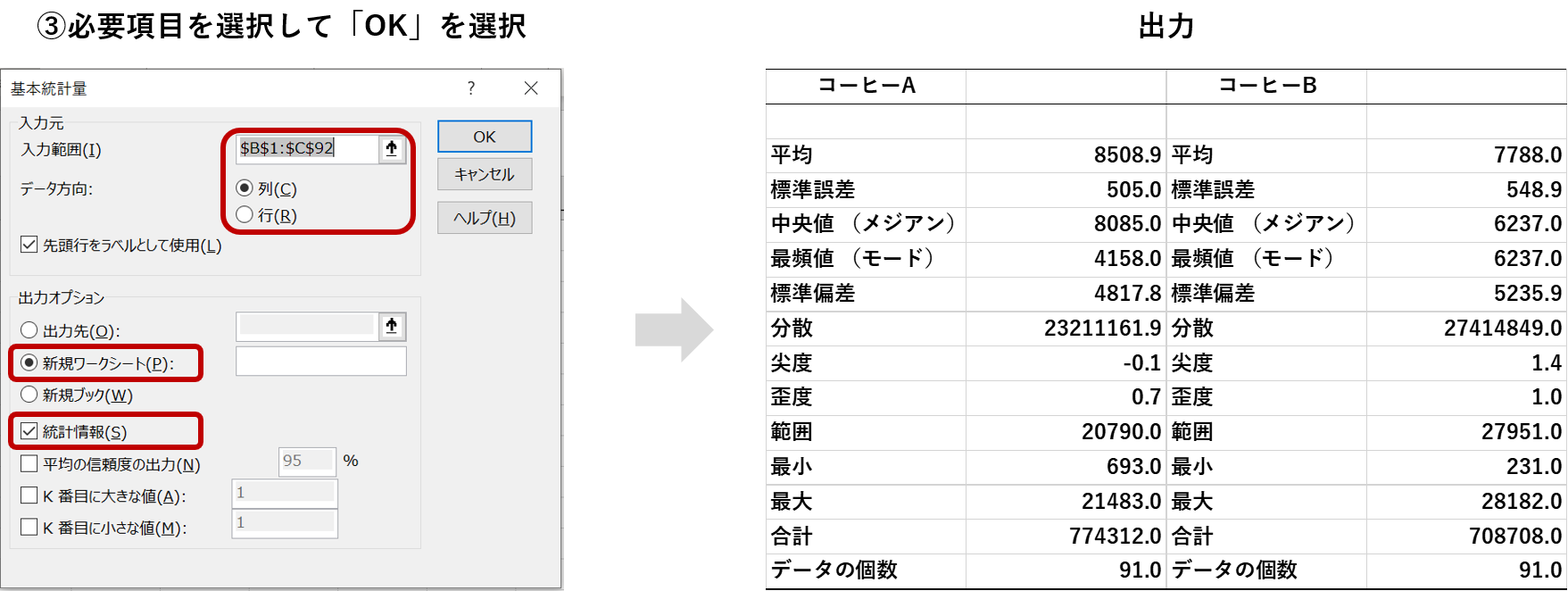
これで基本統計量が出力され、データの概要を掴むことができるようになりました！

分析結果の解釈

出力を見ると、コーヒーAの方が売上平均は高いものの、最高売上はコーヒーBの方が高いことが分かります。実際にコーヒーBの方が分散が大きいことからも、コーヒーBはコーヒーAよりも売上の変動が大きいことが分かります。

ケース②：移動平均で直近数か月の売上の傾向を把握する

使用する手法：移動平均

値の推移の傾向を見やすくするために、移動平均がよく用いられます。

カフェを経営していると、最近の売上が上昇傾向にあるのか下降傾向にあるのか知りたいと思います。しかし4月～6月の3ヶ月間の毎日の売上をグラフに起こすと、グラフがギザギザしてしまってイマイチ傾向を見つけることが難しいことが分かります。

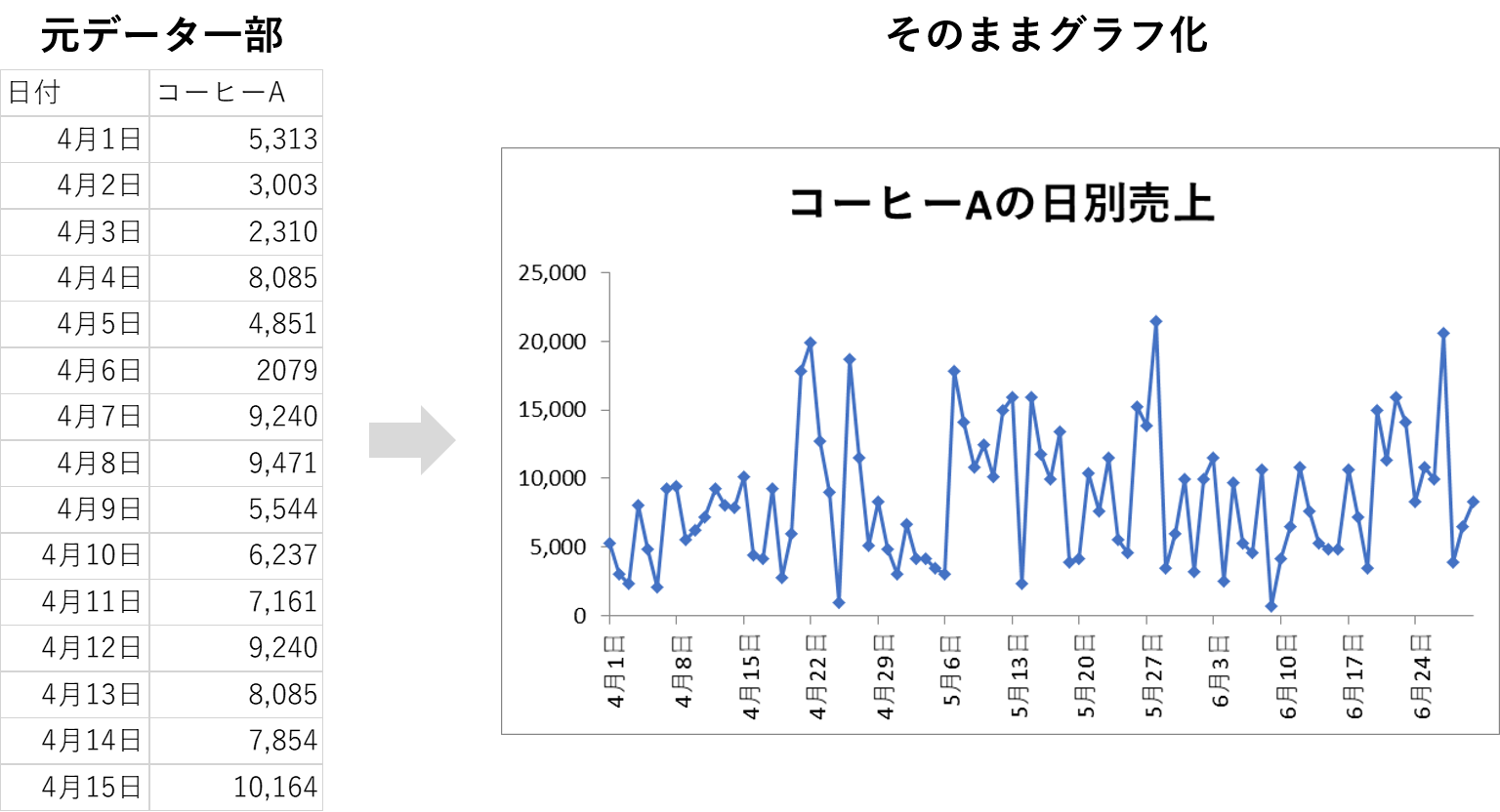
移動平均を利用して、このギザギザを滑らかにし、値の推移の傾向を見やすくしたいと思います。

移動平均とは

移動平均とは、日にちや月を一定区間ずらして平均を求める方法です。例えば3日間移動平均の場合は、算出する日付から前3日分の平均値を当該日付の値とします。

分析を行う

それでは、コーヒーAの売上の移動平均を求めて可視化したいと思います。

まずデータを用意して、「分析ツール」を開き、「移動平均」を選択します。

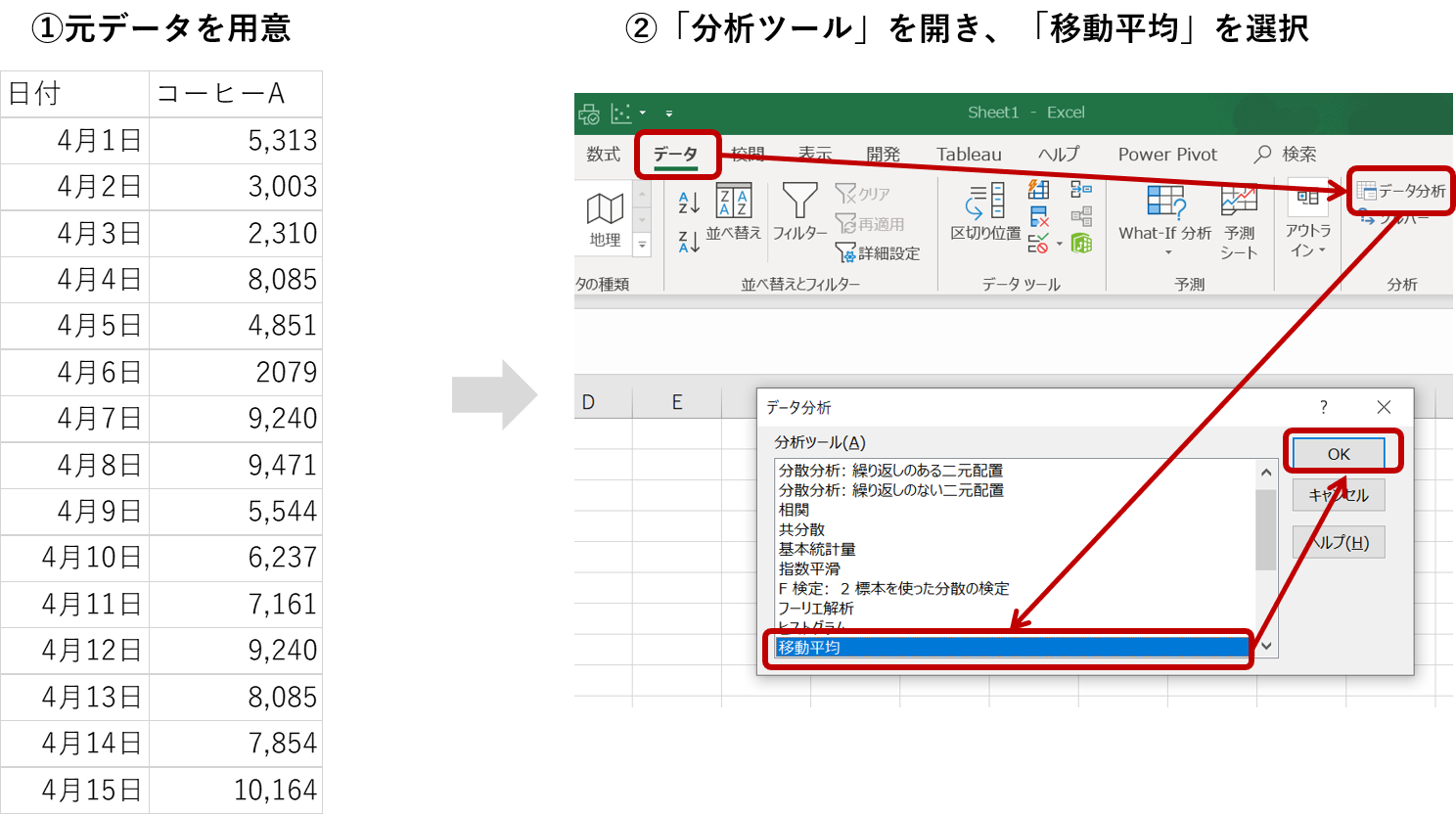
「入力範囲」で分析するデータ（1行もしくは1列のみ）を指定し、以下のように設定して「OK」を選択すると結果が出力されます。なお今回は7日間移動平均を見るために「区間」の項目を7と設定しています。

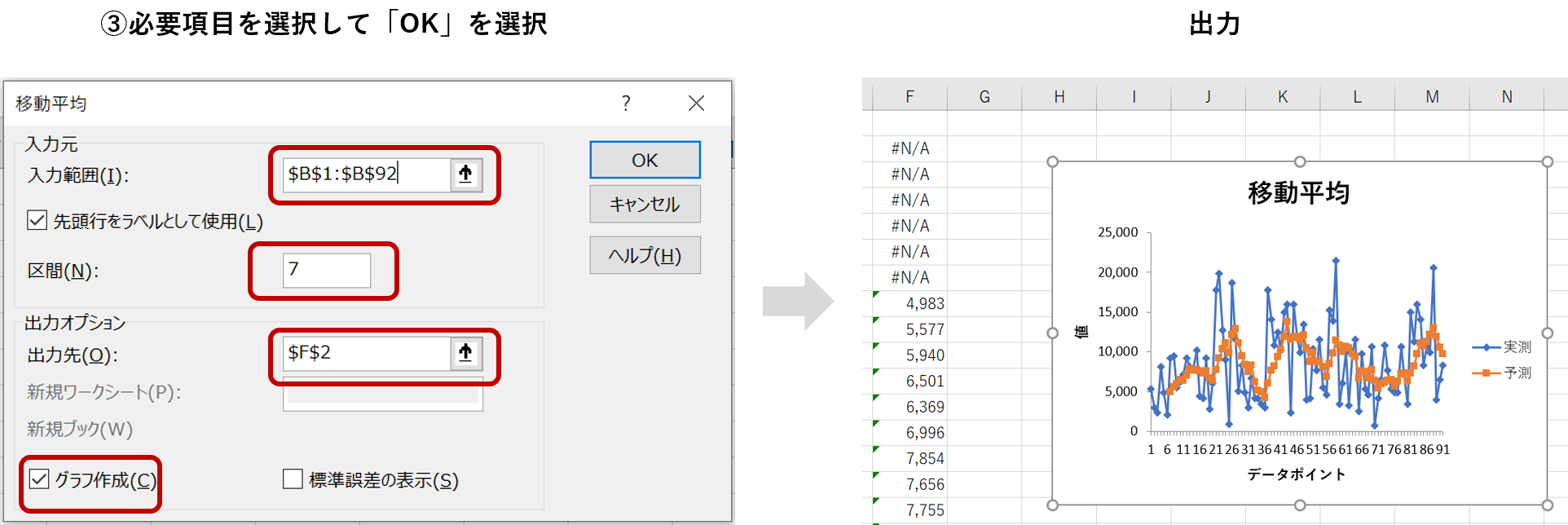
出力の図から、各日付の移動平均が算出され、滑らかな移動平均線が描かれていることが分かります。

分析結果の解釈

オレンジ色の移動平均線が徐々に右肩に上がっていることから、このカフェのコーヒーAの売上は増加傾向にあるといえそうです。

ケース③：ヒストグラムで一回当たりの購買金額の分布を見る

使用する手法：ヒストグラム

値がどの層に密集しているかを把握するために、ヒストグラムは非常に有効な手段になります。

売上を増やすにあたって、客単価を上げることは一つの課題です。今回分析するカフェでも客単価を上げるために、「700円くじ」を導入したいと考えます。この「700円くじ」は、700円以上の購買をした顧客にくじを引いてもらい、くじに記載された賞名に沿って景品を渡すというものです。コンビニでよく行われている手法です。

さて、この700円という価格設定は果たして適切なのでしょうか？もし購買額のメイン層が300円付近ならば、700円は高めの価格設定です。反対に1000円付近の購買が一般的ならばこの施策が平均購買単価を高めるとは考えにくいです。

そこで、ヒストグラムを使用して適切な価格を考えたいと思います。

ヒストグラムとは

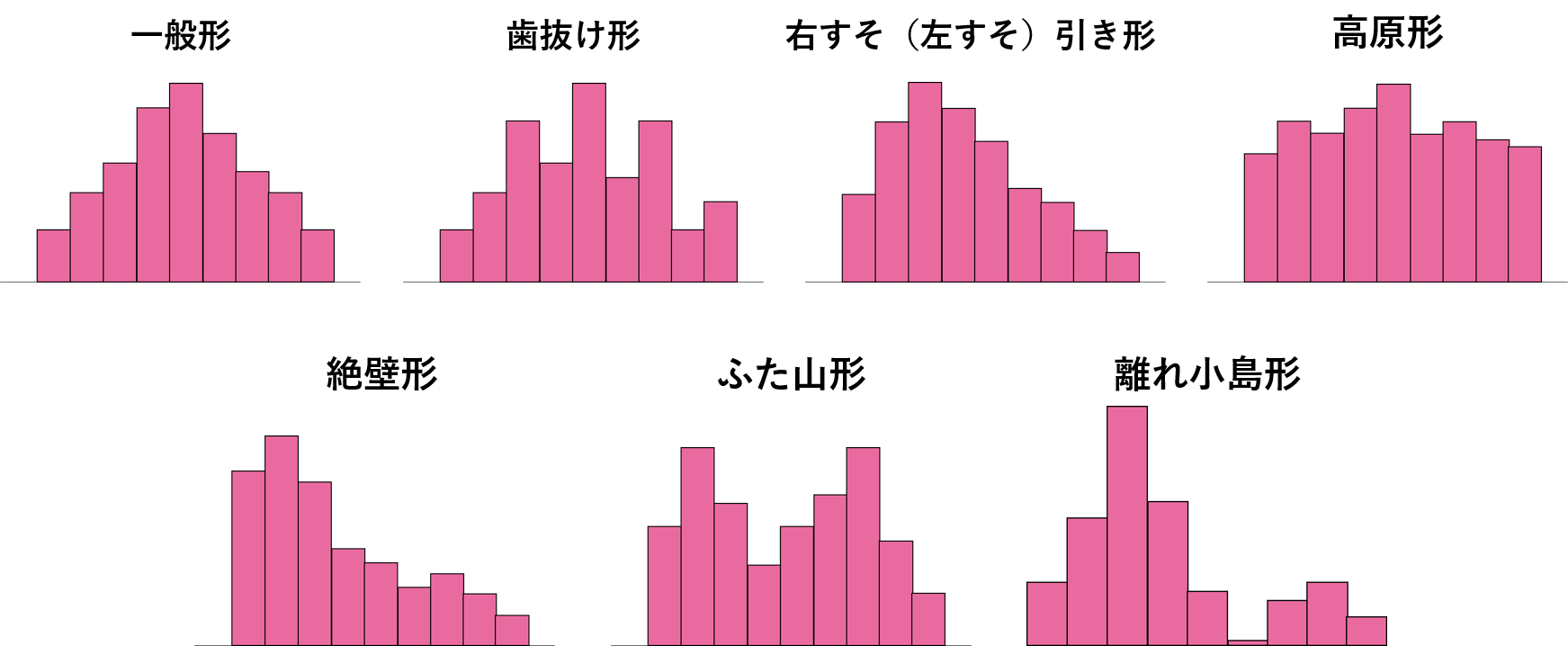
ヒストグラムは、度数分布表を棒グラフのように表した図です。横軸に階級を置き、縦軸に度数を置き、データがどのように分布しているかを把握することができます。

ヒストグラムの形は様々な場合がみられます。以下はその代表例です。

分析を行う

それでは、このカフェの一回当たりの購買金額の分布を求めて700円くじの是非を確かめたいと思います。

まず、データを用意して、「分析ツール」を開き、「ヒストグラム」を選択します。

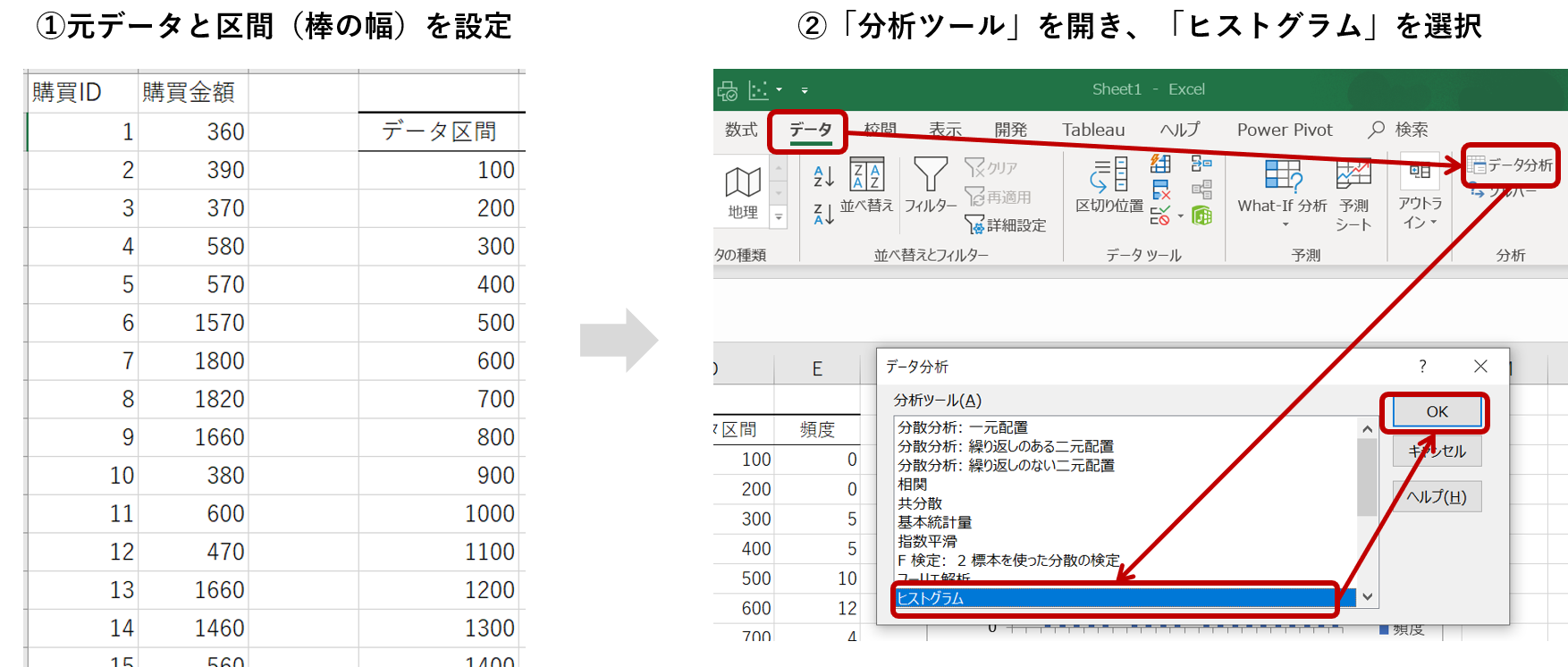
「入力範囲」で分析するデータ（1行もしくは1列のみ）を指定し、「データ区間」にあらかじめ設定した区間（今回は100刻み）を指定します。残りを以下のように設定して「OK」を選択すると結果が出力されます。

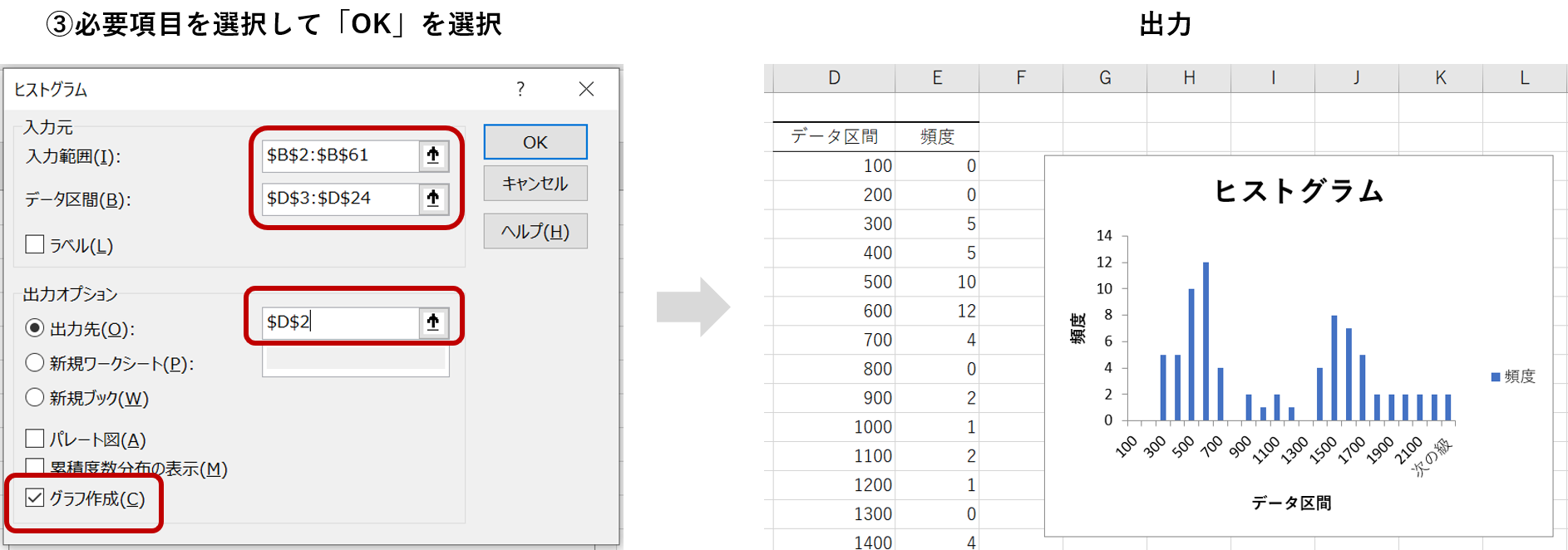
出力の結果、各データ区間に対応するデータの個数と、その個数に対応するヒストグラムが描画されました。

分析結果の解釈

今回のヒストグラムを見ると、2点示唆を読み取れます。

まず1点目が、600円から700円に移る段階で頻度が大きく落ちている点です。このことから600円以下の購買金額で済ませている顧客が多く、700円くじを行うことで平均購買単価を上げることが期待できそうです。

2点目が、1500円付近で再び盛り上がり、1800円から1900円に移る段階でまた頻度が落ちる点です。つまりこのカフェでは600円付近の低額購買層と、1500円付近の高額購買層に分かれることが分かります。この結果から、700円のほかに、「2000円の購買で3回くじが引ける」といったキャンペーンを打つことが有効なのではないかと考えられます。

ケース④：相関分析で気温と商品の売上に相関があるのかを調べる

使用する手法：相関

データ間の変動の一致を調べるのに、相関分析がよく用いられます。

夏にホットコーヒーを飲む人はあまり見かけませんが、冬場でもアイスコーヒーはちらほら見かけます。もし気温が下がっても売上が落ちないのであれば、ある程度アイスコーヒーは用意しておかなければなりません。

そこで気温とアイスコーヒーのデータから、両者の変動の関係性を調べたいと思います。

相関とは

2つのデータAとBに関して、Aが増えたときにBも増える傾向にあれば「正の相関」、反対にAが増えたときにBは減少する傾向にあることを「負の相関」があるといいます。各データの動き方の共通性を見たいときに用いる手法です。

分析を行う

それでは、気温とアイスコーヒーの売上に相関があるかを求めていきます。今回はお店で取り扱っているコーヒーA、B、Cの3種類を見ていきます。

まず、データを用意して、「分析ツール」を開き、「相関」を選択します。

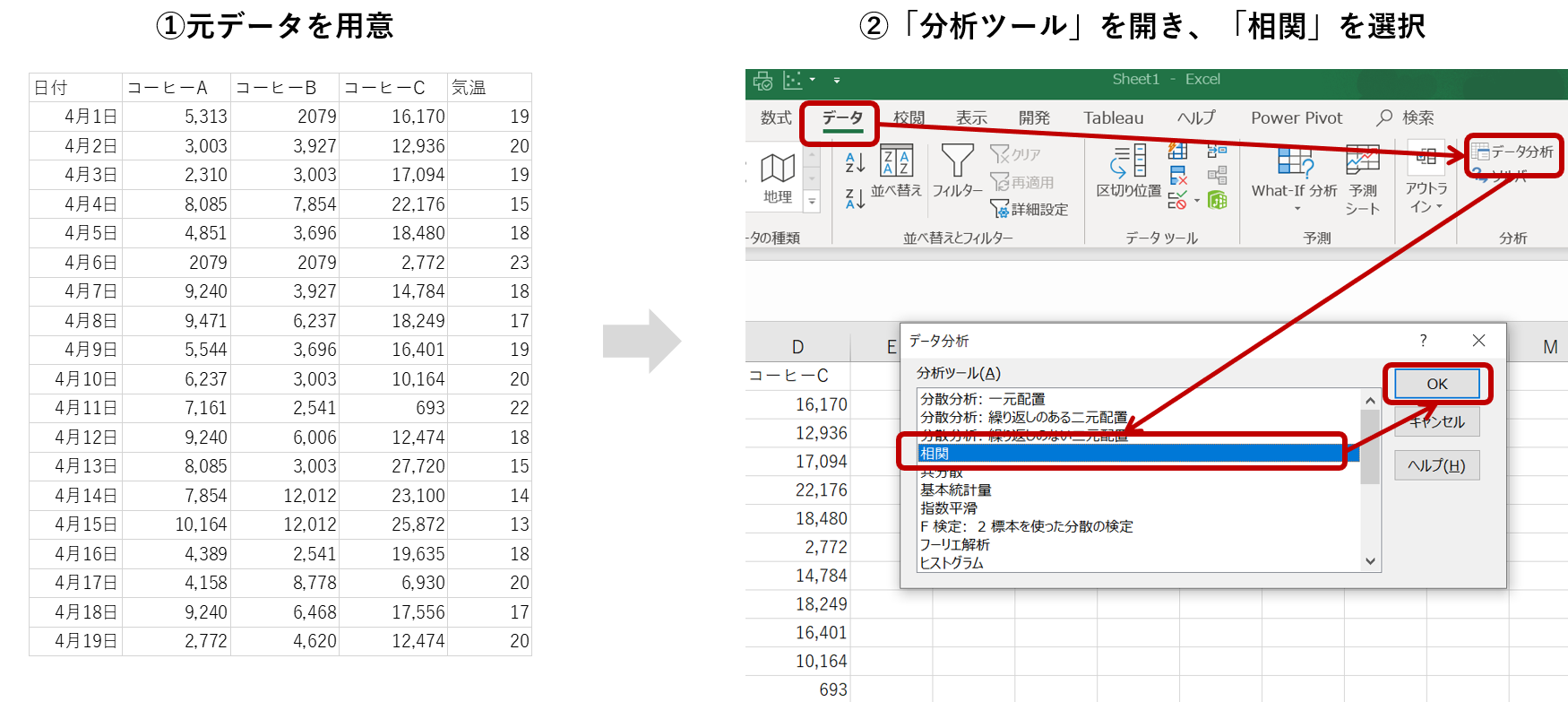
「入力範囲」で分析するデータを指定し、必要個所に入力をして「OK」を選択します。この時、列名（先頭行）を含めておくと結果が見やすくなります。（見やすさのために最小限の編集を行っています）

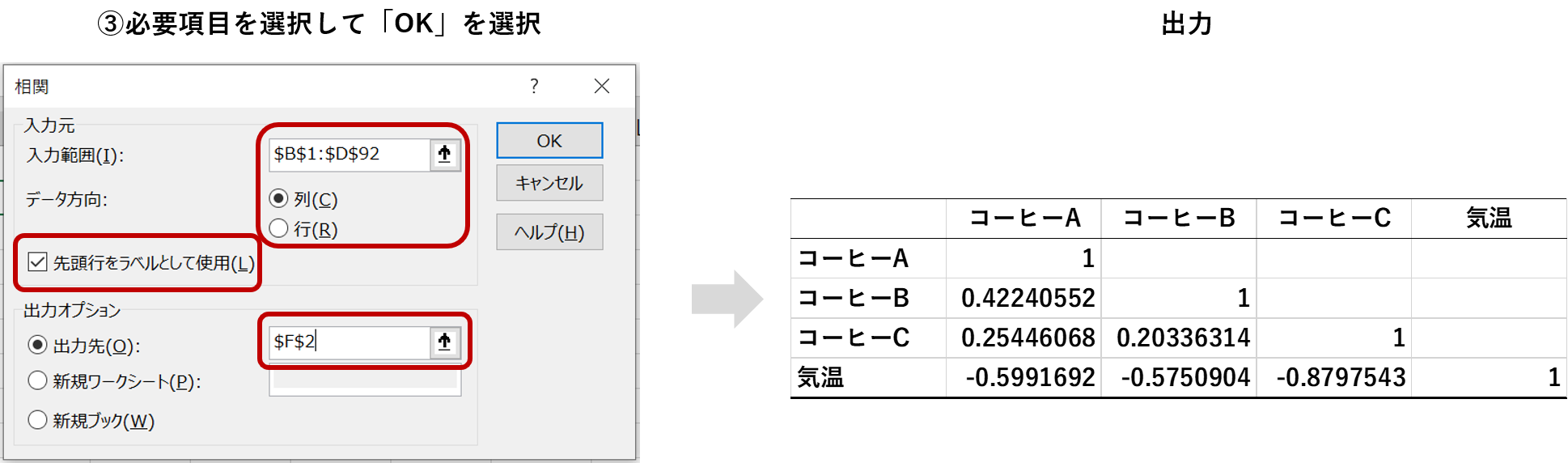
出力は表の左下が埋まった形で出てきます。各セルに表示されている値は、その節の行と列それぞれの項目間の相関係数を表しています。

相関係数は、1に近いほど「正の相関」がある、－1に近いほど「負の相関」がある、0に近いほど「相関関係がない」と読み解きます。

分析結果の解釈

出力の表の最後の行を見ると、気温はどのコーヒーに対しても「負の相関」にあると分かります。このことから、どのコーヒーも気温が下がると概ね売上が落ちるということが分かりました。特にコーヒーCは相関係数が-0.88と大きいことから、気温の影響を激しく受ける商品だということが分かります。

ケース⑤：t検定で2つの商品の売上に差があるのかを調べる

使用する手法：F検定、t検定（分散が等しくないと仮定した2標本による検定）

2つの対象に関してそれぞれの平均値に「偶然とは言えない差」があるのかどうかを調べるのに、t検定を用います。

ここのカフェには、コーヒーAとコーヒーBの2つのレギュラーメニューがあります。そしてここ最近業績が振るわず、この2商品のうち片方をメニューから取り除く決断をしました。

しかしどちらを除くべきかが少し悩んでいます。ケース①の分析で、平均売上高はAの方が高いのですが、最高売上はBの方が高いのです。平均売上が高い方を選びたいのですが、もしかしたら①で出た平均の差はたまたまなのかもしれないという不安が残ります。なので「Aの方が売上平均が高い！」と断言できる材料が欲しいと考えています。

そこで、t検定を用いて「Aのほうが売上平均が高い！」かどうかを確かめます。またこのt検定を行う前段階としてF検定というものも行われます。

t検定とは

t検定は「母平均に対する検定」と呼ばれます。「今年の桃は例年より重いか」、「AとBのクラスで数学の平均点数に差はあるのか」など、平均値の差に関する問いに答えてくれる手法です。

F検定とは

F検定は、比較するデータ間のばらつき（＝分散）が等しいかどうかを検定する手法です。このF検定の結果次第でt検定で用いる手法が変わります。

分析を行う

それでは、コーヒーAとコーヒーBの売上に差があるのかを調べてみます。

まず初めにF検定を行い、コーヒーAとコーヒーBの売上のばらつきが同じかどうかを確認します。

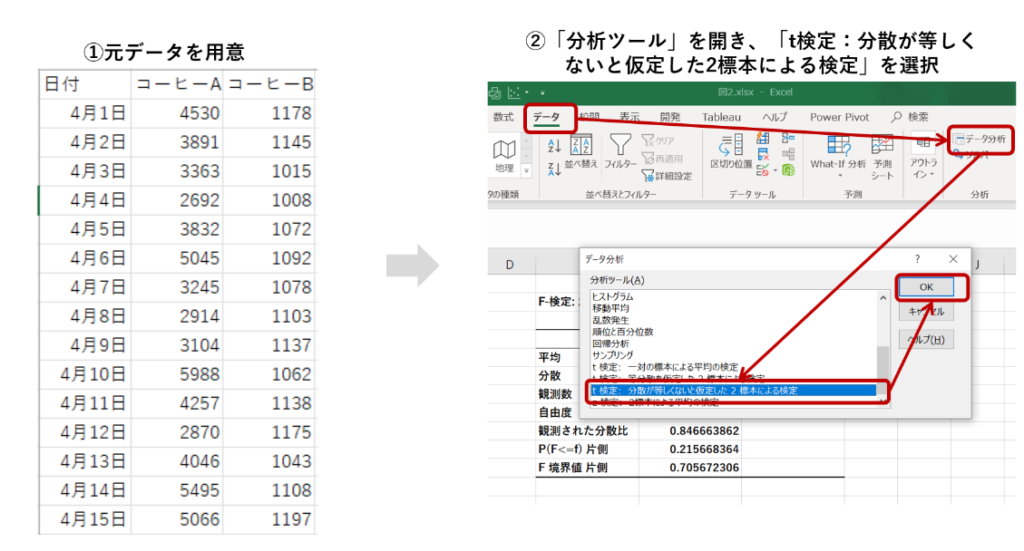
データを用意して、「分析ツール」を開き、「F検定」を選択します。

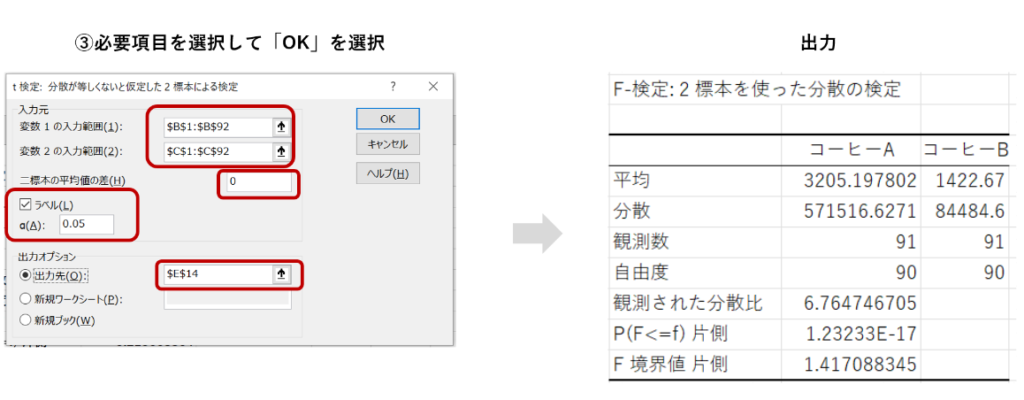
「入力範囲」で分析する2つデータ列をそれぞれ指定し、必要個所に入力をして「OK」を選択します。先頭行に商品名があるのでラベルにはチェックを付けます。

また、α（A）は分散が等しいかどうか判定するための閾値になります。通例0.05や0.001が選択されることが多いです。出力のP値がこのα（A）を上回れば2つのデータの分散は等しいとされ、反対にP値がα（A）を下回れば2つのデータの分散は等しくないと結論付けます。

出力結果を見ると、P値は1.23233E-17(<0.05)となっています。1.23233E-17は1.23233かける10の-17乗です。このことから、コーヒーAとコーヒーBの売上のばらつき（＝分散）は等しくないことが分かります。

そのため、今回は「分散が等しくないと仮定した2標本による検定」用いて平均の差の検定を行います。

t検定を行う

それではt検定を用いて、コーヒーAとコーヒーBの売上に差があるのかを確かめてみます。

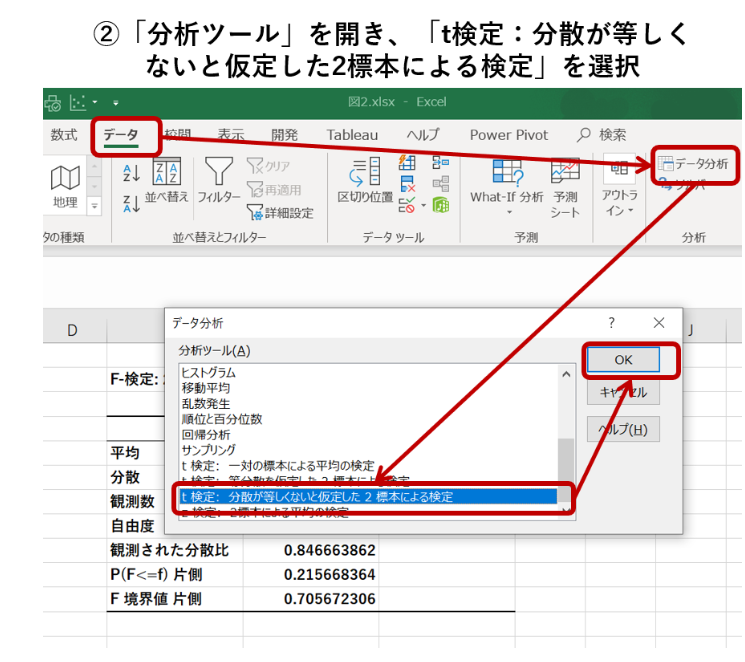
先ほどと同じデータを用意して、「分析ツール」を開き、「t検定：分散が等しくないと仮定した2標本による検定」を選択します。

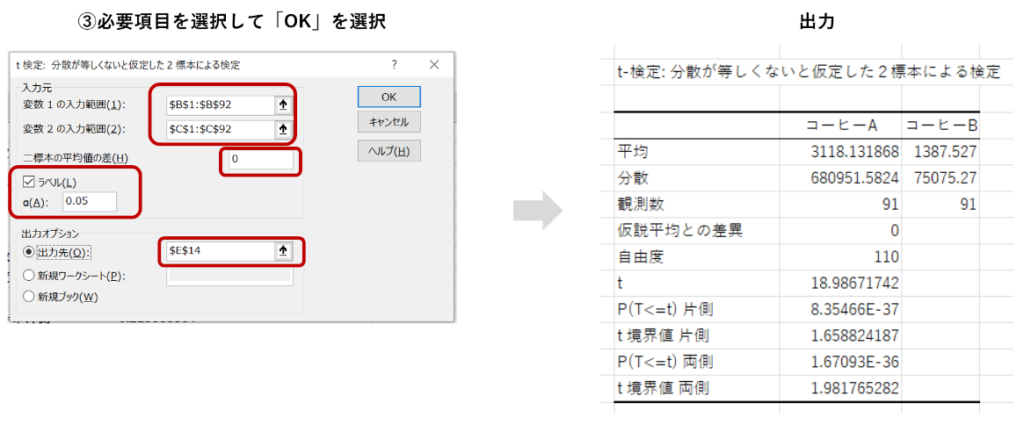
「入力範囲」で分析する2つデータ列をそれぞれ指定し、必要個所に入力をして「OK」を選択します。基本的にF検定の時と同じ設定で問題ありません。

「二標本の平均値の差」の項目には、今回は0を入力します。2つの平均値の差が「0か否か」を確認したいので0が選択されます。

出力結果には10個ほどの指標が並んでいます。今回注目する値は「P(T<=t)片側」です。今回の目的が「コーヒーAの方がコーヒーBより売上平均が高い」という片方の値の大小に注目したものなので、「片側」の指標を見ることになります。

そしてこの値が設定したα（A）よりも小さければ、2つの平均に差があるといえます。

分析結果の解釈

出力された「P(T<=t)片側」の値は8.35466E-37(<=0.05)なため、2つの売上平均に差があると言えそうです。

ケース⑥：分散分析で複数商品の各売上に差があるのかを調べる

使用する手法：分散分析（一元配置）

先のケース⑤では2種類の商品に関して売上平均の差を見ました。

しかしこのカフェにはコーヒーA、コーヒーB、コーヒーC合計3種類のコーヒーがあります。この3種類を並べて差があるかも確かめたいです。

しかしt検定では一回に2種類までしか見ることができないため、3種類すべてを見るにはt検定を3回行わなければなりません。これでは面倒ですね。

このように、3種類以上のデータに対してその平均に差があるかを確かめるときは、分散分析を用います。

分散分析（一元配置）

まず分散分析は、分散の大きさを用いて各平均に違いがあるのかを調べる手法です。比べたいデータが3種類以上あるときに用いられます。

分散分析には大きく分けて、一元配置と多元配置（主に二元配置）と呼ばれるものがあります。「〇元」というのは、要因の数のことを指します。

今回の例であれば、売上平均の差を見る要因は商品の種類という一要因のみなので、一元配置となります。これに地域や店舗規模などの要因が加わると多元配置になります。多元配置に関しては次のケース⑦で扱います。

分析を行う

それでは、コーヒーA、コーヒーB、コーヒーCの3種類のコーヒーの売上に関して差があるのかを調べてみます。

コーヒーのデータを用意して、「分析ツール」を開き、「分散分析：一元配置」を選択します。

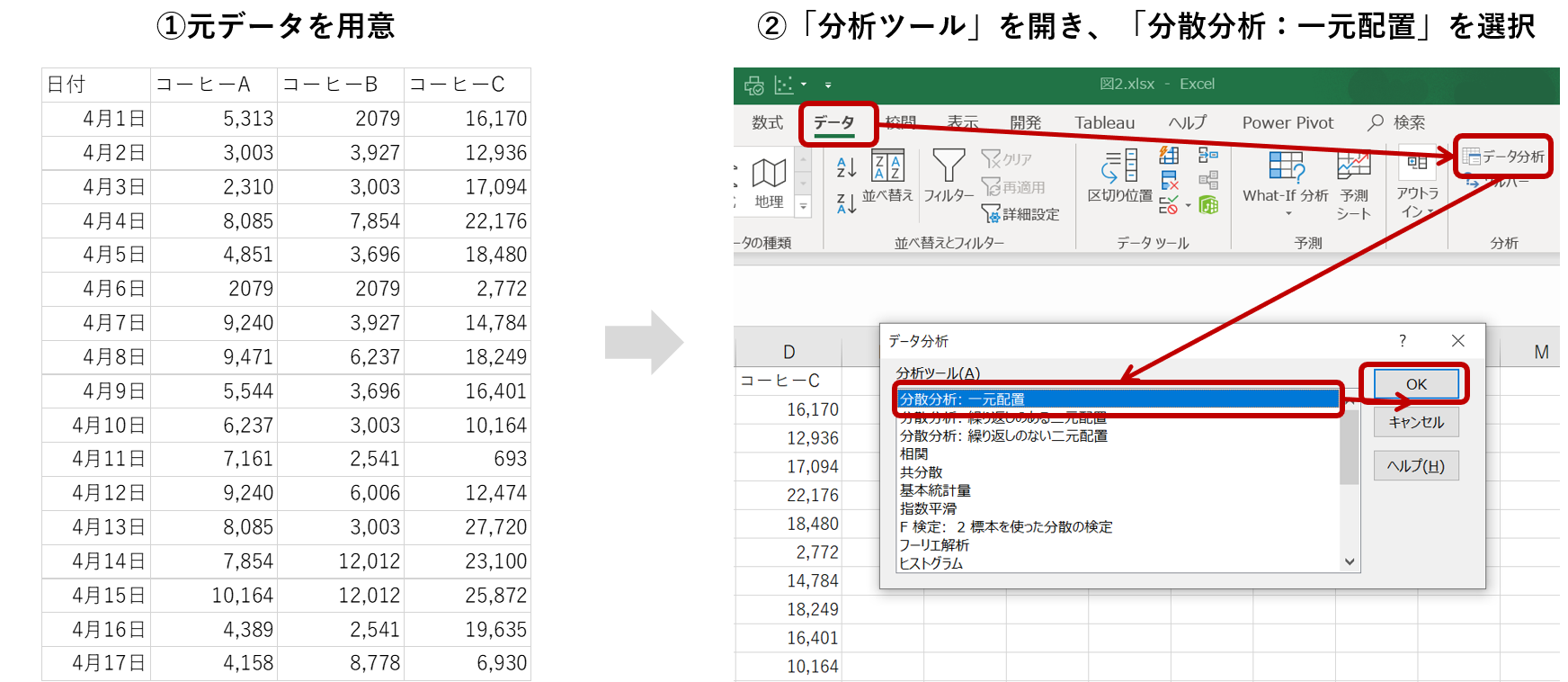
「入力範囲」で分析する2つデータ列をそれぞれ指定し、必要個所に入力をして「OK」を選択します。t検定とは異なり対象データを一括で範囲に指定します。

また今回もα（A）は0.05に設定しています。

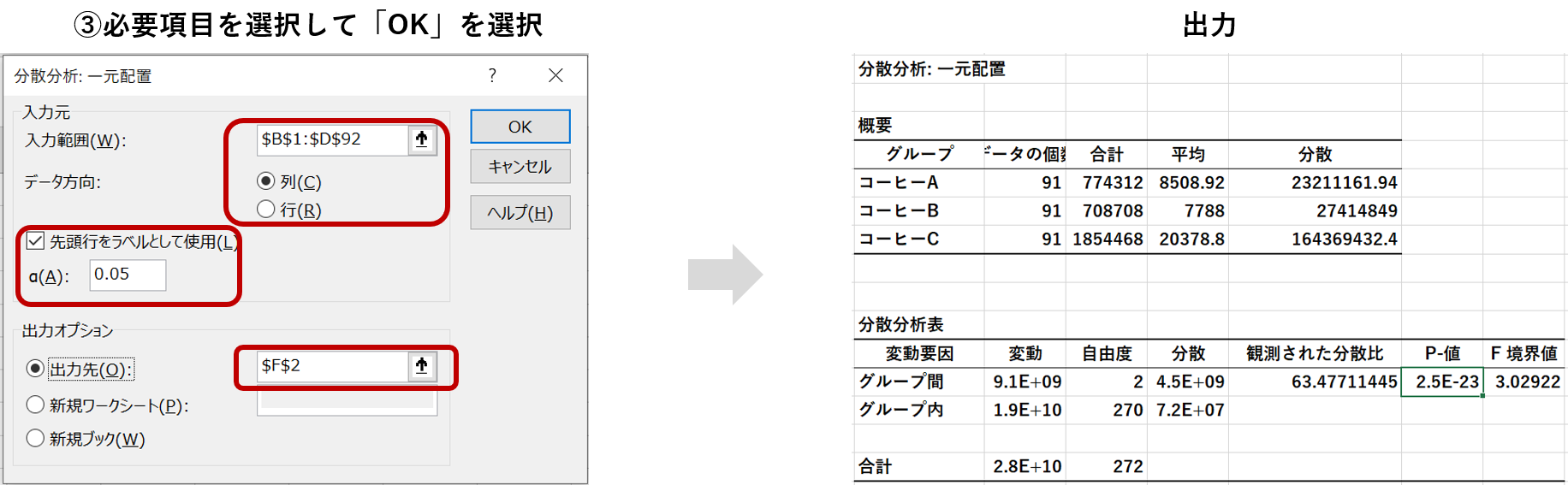
今回の出力で注目するのは「P値」です。この値が先ほど設定したα（A）より小さければ、3種類の商品の売上平均に差があるということができます。

分析結果の解釈

出力された「P値」は2.5E-13です。これは0.05より小さな値なため、3種類の商品間の売上平均に差があるといえそうです。同じ表の「平均」の欄を見ると、コーヒーCの売上金額がずば抜けて高いです。そのためこのコーヒーCの突出具合が今回の結果の要因になったと考えられます。

ケース⑦：分散分析で曜日と商品に関係性が”あるのかどうか”を調べる

使用する手法：分散分析（繰り返しのない2元配置）

商品や曜日などの2要因に関して関係性があるのかどうかを見たいとき、二元配置の分散分析を用いることができます。

商品を買いたいお客さんがいるのに、在庫がないことは大変な機会損失です。しかし持てる在庫は限られているため、よく売れる曜日があれば、その曜日には多く在庫を用意し、そうでない日は他の商品の在庫を優先したいと考えています。

分散分析を用いて曜日による売上の違いを見たいと思います。

二元配置の分散分析とは

ケース⑥で説明した通り、2元配置の時は値の差に影響する要因が2つの時を言います。今回のケースであれば、「商品の違い」と「曜日」の2種類の要因に注目しているので2元配置になります。

またこの2元配置にも、「繰り返しがある二元配置」と「繰り返しのない2元配置」があります。

「繰り返しのない2元配置」は各要因の組み合わせに対して値が1つしかないのに対して、「繰り返しのある2元配置」は複数の値があるものをいいます。

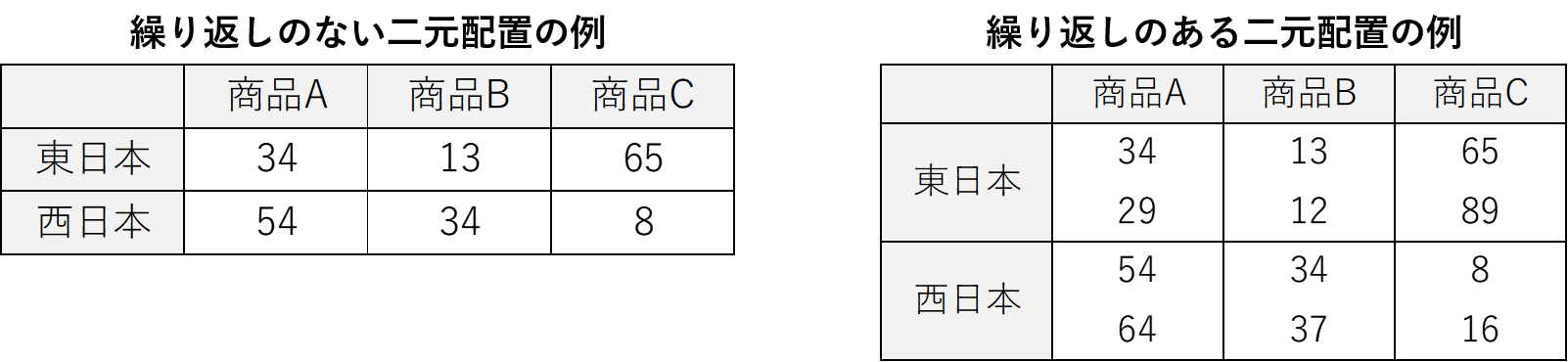
今回の分析では「繰り返しのない」データを使用するので、「繰り返しのない二元配置」の分散分析を行って差を確認していきます。

分析を行う

コーヒーA、コーヒーB、コーヒーCの3種類のコーヒーの売上平均に関して、曜日という要因を加味して差があるのかを調べてみます。

曜日×商品のクロス集計データを用意して、「分析ツール」を開き、「分散分析：繰り返しのない二元配置」を選択します。

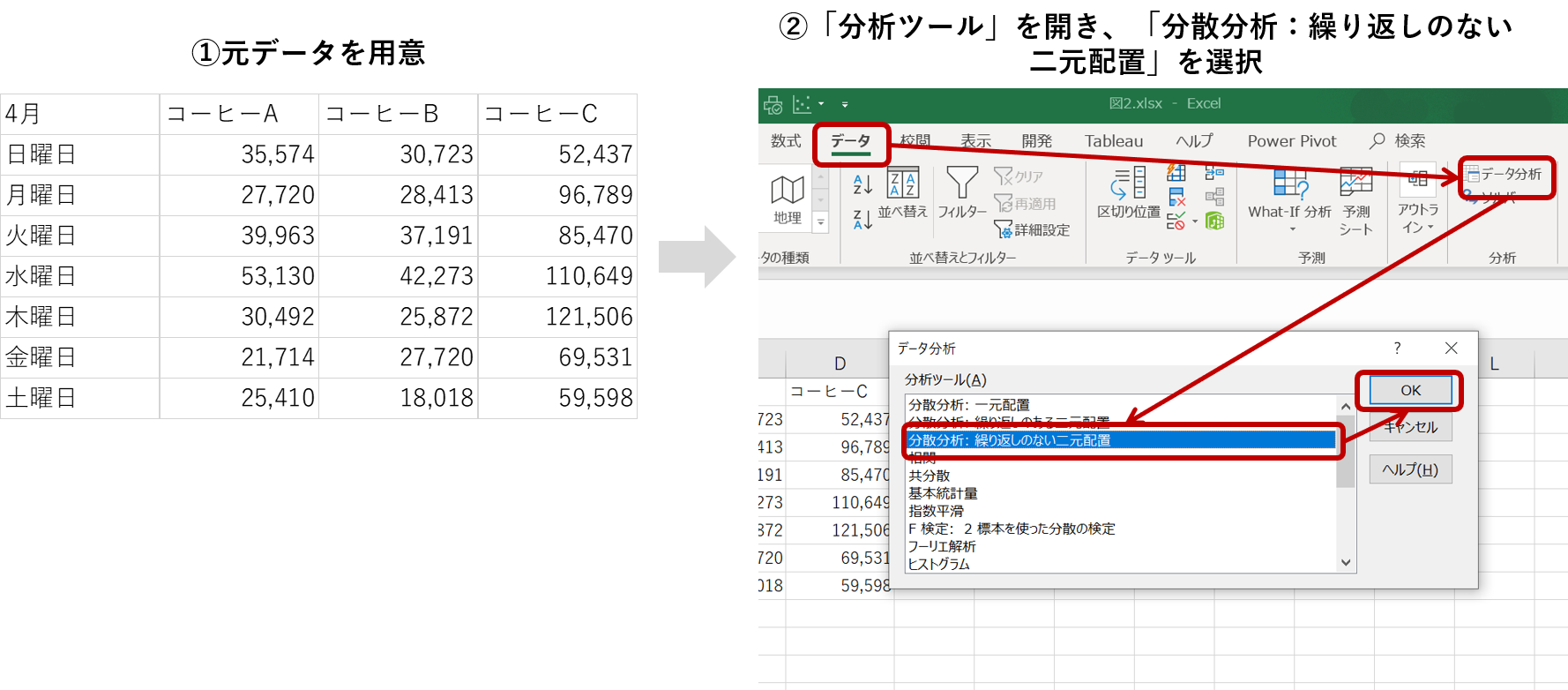
クロス集計表全体を「入力範囲」に指定して、必要個所に記入し「OK」を選択します。今回もα（A）は0.05としています。

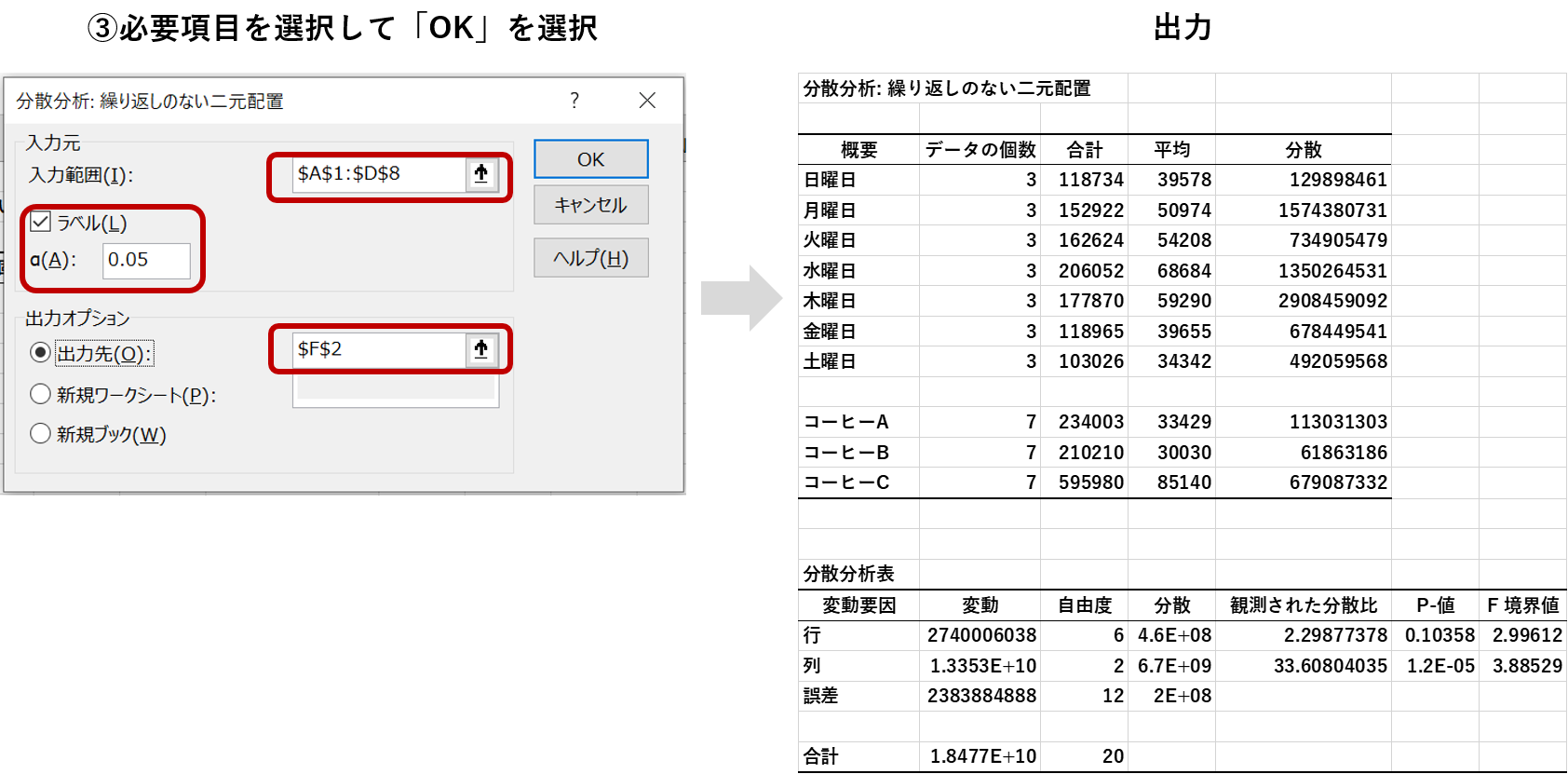
今回の出力先でも注目すべきは「P値」です。行（曜日）と列（商品）についてそれぞれこの「P値」が先ほど設定したα（A）より小さければ、その要因によって売上平均に差が出ていると言うことができます。

分析結果の解釈

まず行（曜日）の「P値」は0.103 (>0.05)なため、売上に影響を及ぼしているとは言えなさそうです。

次に列（商品）の「P値」は1.2E-05 (<0.05)なため、売上の差に影響している要因といえます。この結果はケース⑥と一致していることが分かります。

これにより、曜日に関係なく均等に在庫を用意したほうがいいことがわかります。

ケース⑧：回帰分析で売上に最も影響を与えている施策は何かを探る

使用する手法：回帰分析 

「どの要因が売上に結び付いているのか」を推定する手法の一つに、回帰分析というものがあります。

チラシやメールやツイッターなど、お店のプロモーションを行う手段はたくさんあります。それら手段を組み合わせて認知を浸透させるとともに、最終的に来客数を増やしたいと考えています。

今現在、このカフェではLINE・Facebook・ツイッター・チラシの4つを利用して告知を行っています。しかしこの4つのうち、どれが直接的に来店に影響するかが分かっていないのが現状です。もし最も影響のある媒体が分かればもっと積極的にその媒体を利用し、反対にあまり影響のない媒体があれば面倒なので取りやめることも考えられます。

回帰分析を行ってそうした媒体を特定してみましょう。

回帰分析とは

回帰分析は、「他方のデータを用いて、一方のデータを予測する数式を推定する」分析です。例えば家賃を予測したいときに回帰分析を行うことで、家賃以外の情報を利用して家賃を予測する事ができます。この時、下のような回帰式が算出されます。

今回の分析では、式の左側に来るのが売上で、右側に来るのが各媒体の情報になります。

分析を行う

各媒体の情報から、どの媒体が最も売上に寄与しているか調べてみます。

今回、売上は月次のデータを用います。そして媒体の情報は各媒体の月間の投稿数を使用します。

それでは、2年分の月次の売上と各媒体の投稿数のデータを用意し、「分析ツール」を開き、「回帰分析」を選択します。

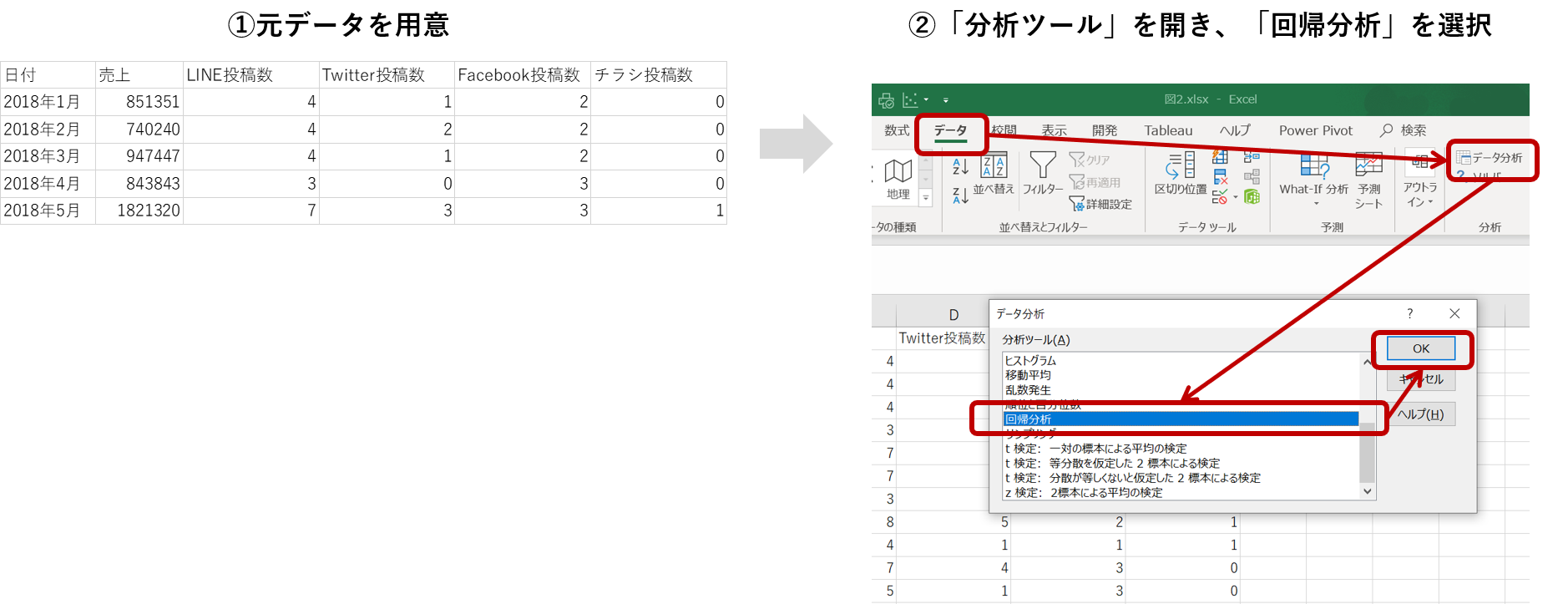
「入力Y範囲」に「売上」の列を指定し、「入力X範囲」に各媒体の列をまとめて指定します。必要個所に記入し「OK」を選択します。

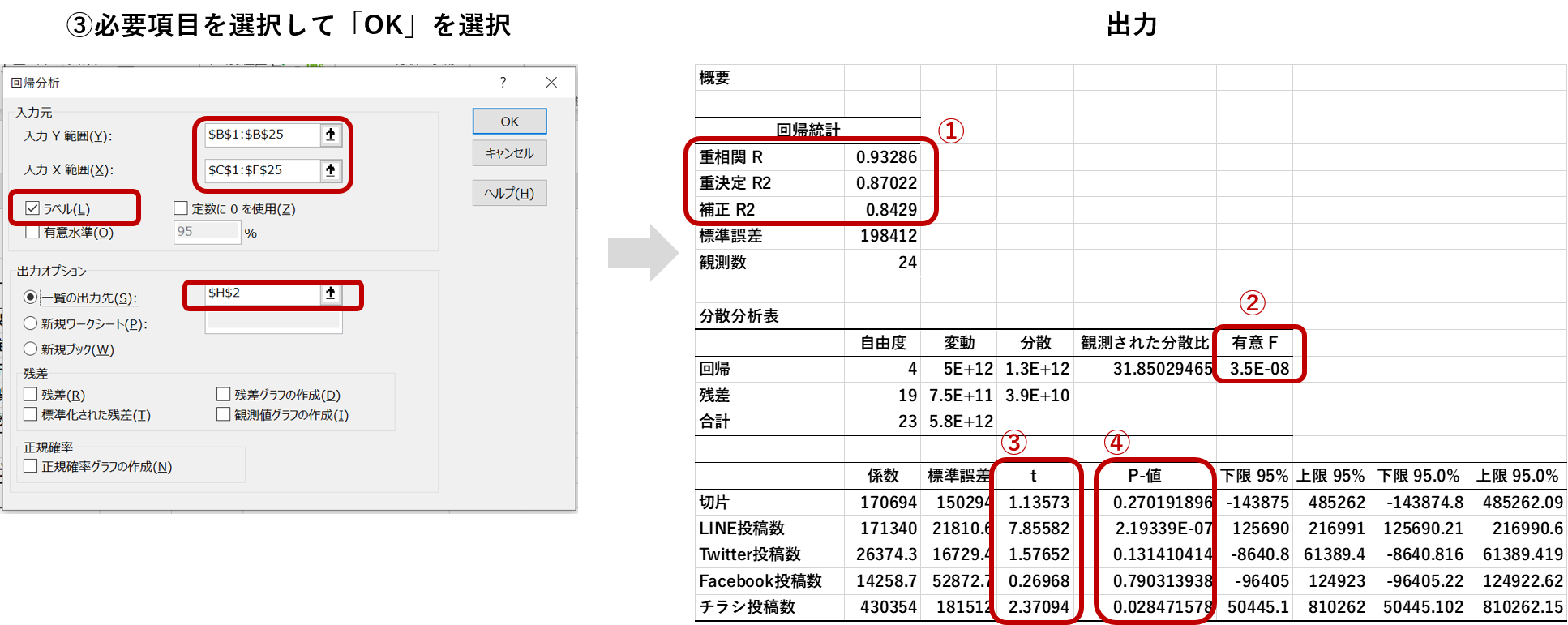
たくさん数字と難しそうな単語が出てきたので、いくつか解説いたします。ここにあるすべての指標を見なくても、分析内容は理解できます。

分析結果の解釈

まず➀決定係数（出力の表の重決定R2）を確認すると、0.87とわかります。これは得られた回帰式が売上の変動の87%を説明していることを表すので、まずまずの精度の回帰式が得られたといえます。

次に②有意Fを確認すると、3.5E-08 (<0.05)より、得られた回帰式が有用なものであると分かります。

次に➃P値を確認すると、LINEとチラシは0.05を下回り、そのほかは0.05を上回っています。そのため、LINEとチラシ以外を売上の要因として考えるのは危険という判断ができます。

最後に、LINEとチラシの➂t値を比較します。ラインのt値が7.8なのに対し、チラシのt値は2.3です。このことから、売上に最も貢献しているプロモーション媒体はLINEであると結論付けることができます

5. 「分析ツール」機能にない分析手法は、他ツールを使うべし

「分析ツール」を用いれば、基本的な分析を行うことは可能です。しかし因子分析や主成分分析、クラスター分析などの手法は「分析ツール」機能で実行することができません。

このような分析を行いたい場合、可能ならばプログラミング言語やBIツールといった他のツールの使用を検討することをお勧めします。例えば、無償であればRやPython、有償であればSPSSやSASというツールが代表的です。

他のツールを使用する一番の理由として、エクセル上で手作業での分析は手間がかなりかかってしまうからです。とあるエクセルの解説書には主成分分析を行うのに、10種類以上の式をセルに打ち込み、「ソルバー」という新たな機能を用いて、10ページ近くかけて結果を算出していました。（かなり丁寧な説明だったのでページがかさむのは仕方ないですが、筆者が実際に試したところ1回10分程度かかってしまいました…。）

その一方で世の中には先述したツールのように、数十万行以上あるデータでもコードを数行書くかボタンをポチポチするだけで分析を行える環境がたくさん存在します。

以下の画像はSAS Ondemand for Academicsという統計解析ソフトウェアの操作画面です。各種設定をクリックするだけで高度な統計解析を行うことができます。

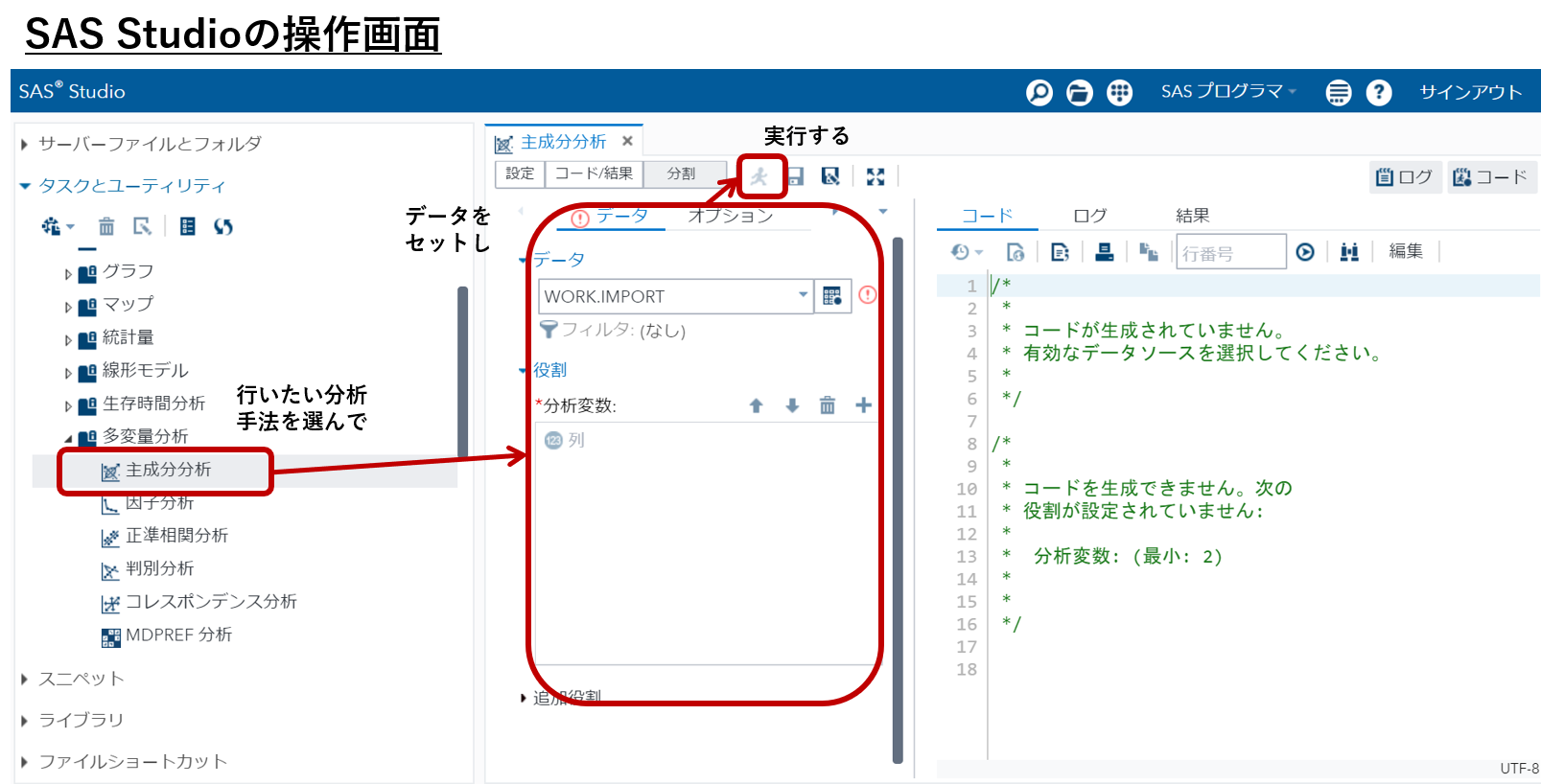
エクセルにはVBAというプログラムを書いて分析を実行できる機能もあります。しかしデータ分析においてはExcel VBAよりPythonのほうがExcel以外でも活用できるという点で、やはりほかのツールに任せるべきです。

新しいツールを学習するには、ある程度の時間のやる気が必要ですが、その投資に見合った分のリターンは得られるはずです。

6. まとめ

エクセルの「分析ツール」機能で8つのケースを分析してみました。

関数など複雑な作業は用いずとも、簡単にデータ分析を行えたと思います。

「分析ツール」機能を活用して、平均値や中央値といった指標を超えた一歩踏み込んだ分析を行い、新たな示唆の発見や素早い意思決定につなげましょう！

データのことなら、高い技術力とビジネス理解を融合させる私たちにご相談ください。

当社では、データ分析/視覚化/データ基盤コンサルティング・PoC支援に加え、ビジュアルアナリティクス、ダッシュボードレビュー研修、役員・管理職向け研修などのトレーニングを提供しています。組織に根付くデータ活用戦略立案の伴走をしています。

データビズラボへ問い合わせする