
この記事では、統計学において最も重要と言っても過言ではないほど重要な定理「中心極限定理」について解説します。この記事を読むことで、中心極限定理がどのような定理なのかを直観的に捉え、なぜこの定理が重要なのか理解することができます。
中心極限定理とは
中心極限定理とは
中心極限定理とは以下の法則です。
※上記のように $n$ を大きくしたとき、分布Aを実質的に正規分布と同じように考えることができる場合、これを「近似」といいます。
これは以下のようにいうこともできます。
この定理において、重要なポイントが2つあります。
- 標本をとってきた元の集団(母集団)が正規分布に従っていなくとも、標本の数が大きくなるに連れてサンプル(標本)の平均値は必ず正規分布に近づいていく
- そのとき標本の平均値の分散は、元の集団の分散( $\sigma^2$ )をサンプルの数( $n$ )で割った値( $\frac{\sigma^2}{n}$ )になる
※正規分布とは、多くの社会現象、自然現象が従う釣鐘上の確率分布です。詳しくは以下の記事を参照してください。
それでは、具体例を見てみましょう。
具体例①
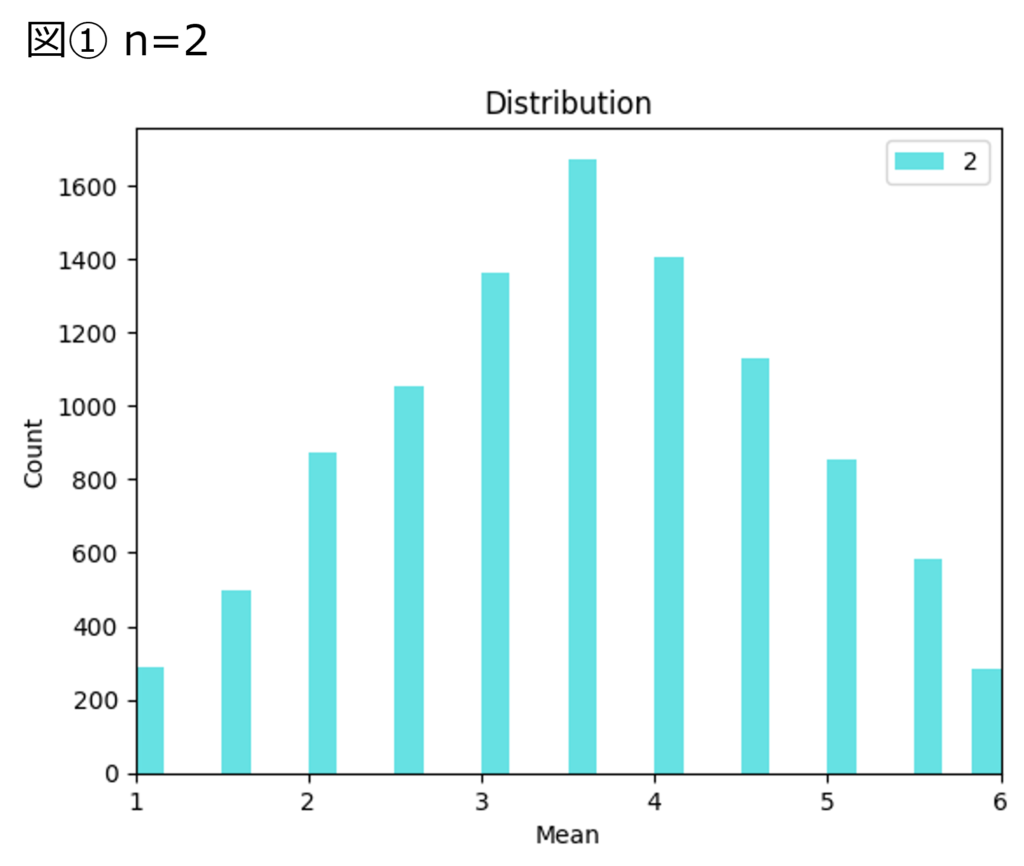
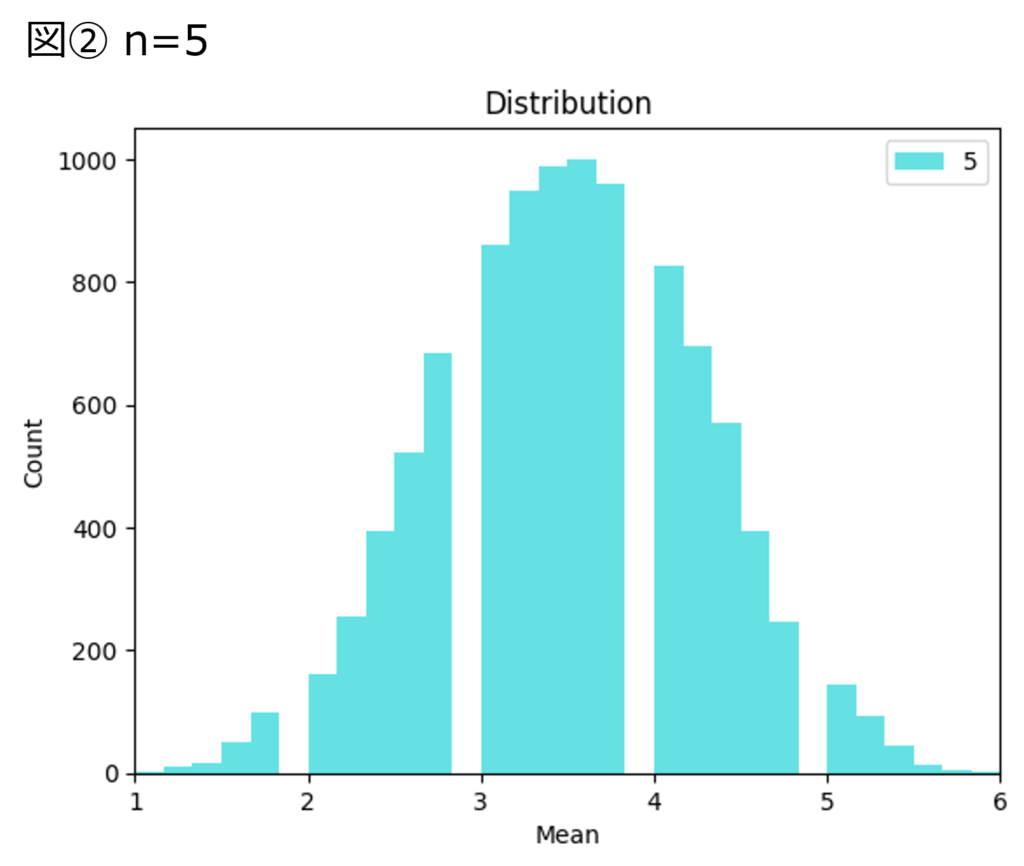
1~6までの各目が同じ確率で出るサイコロを $n$ 回振り、出た目の平均の分布を調べます。$n$ を2、5、100の3パターンとして分布を調べると、以下図①~③のようになります。
$n$ が大きくなるにつれて、サイコロの目の平均の分布は正規分布の形に近づいてく様子が見て取れます。
サイコロの各目が出る確率は、全て1/6であるため、サイコロの目は一様分布に従っています。サンプルを抽出した元の集団が一様分布に従う集団でも、サンプルの平均は正規分布に近づいていきます。
具体例②
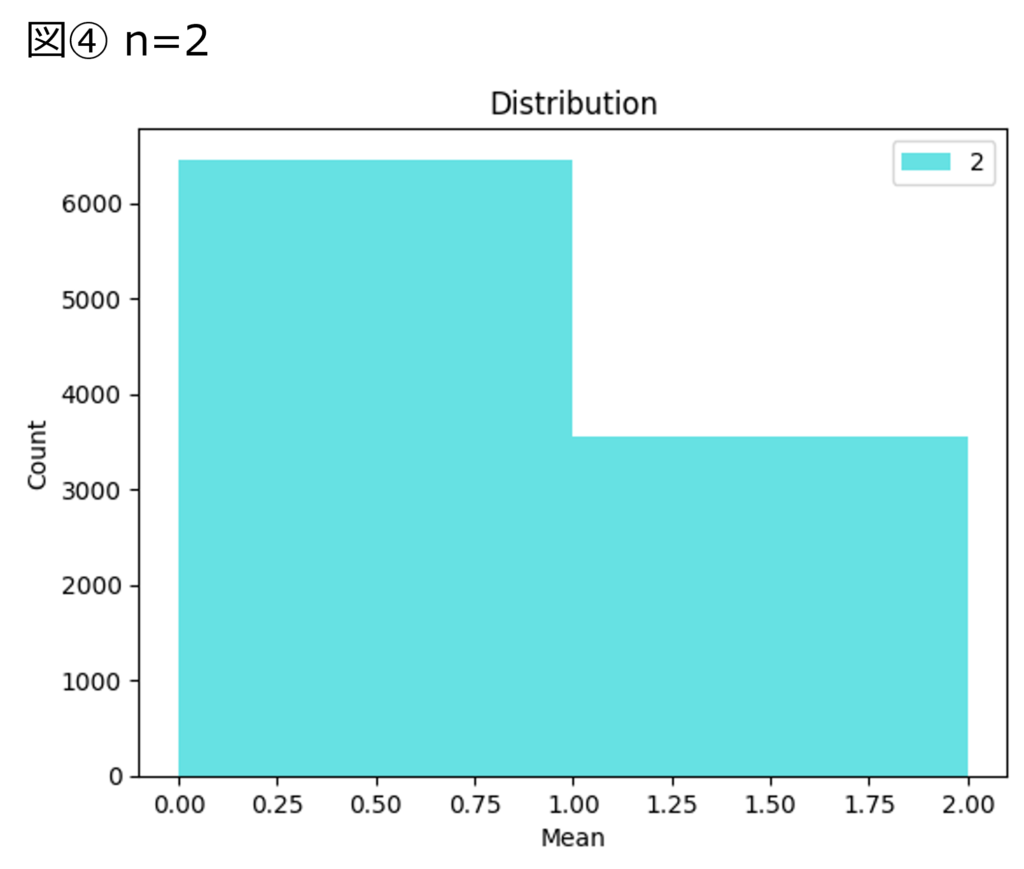
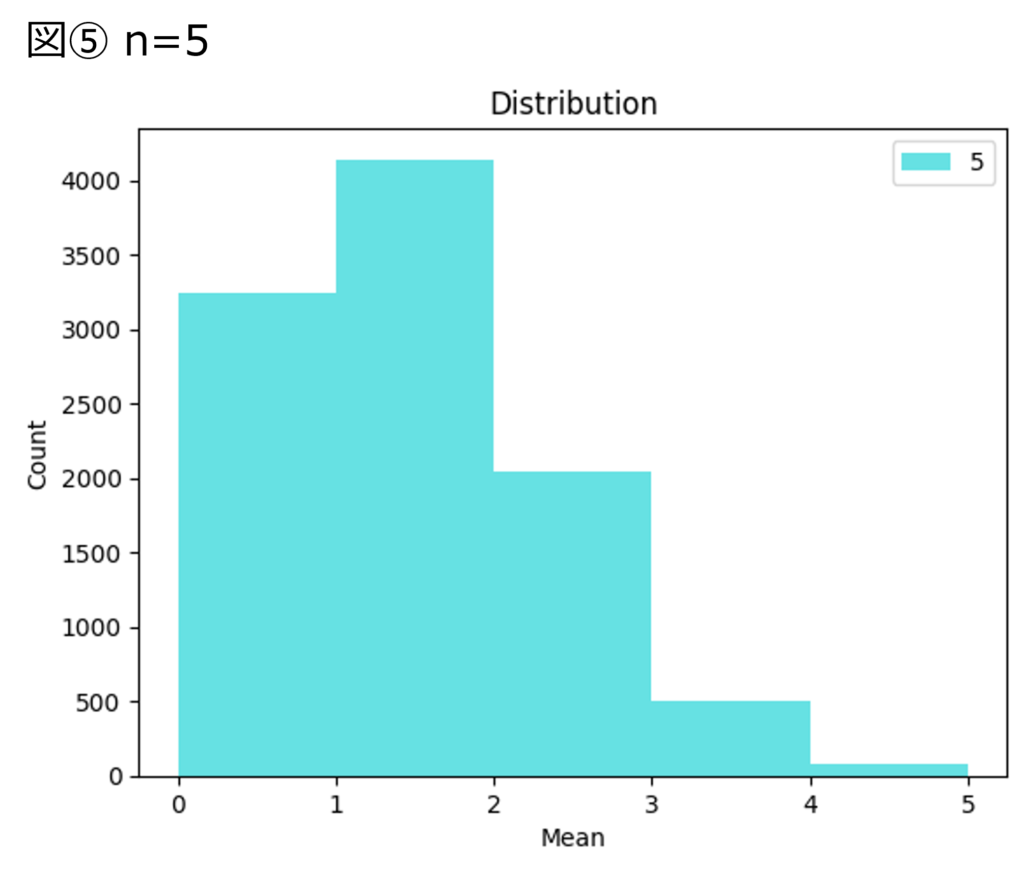
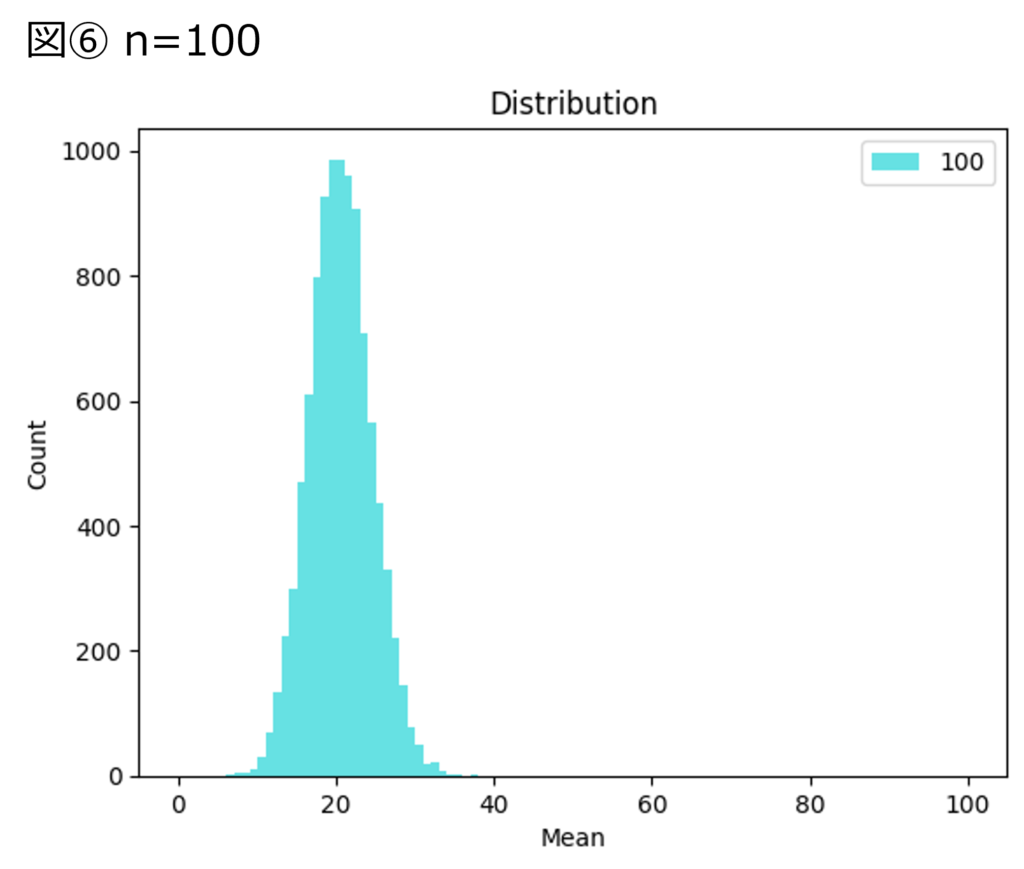
当たりくじが2割、外れくじが8割入った袋から $n$ 回くじを引き、当たりくじの枚数(の平均)の分布を調べます。 $n$ を2、5、100の3パターンとして分布を調べると、以下図④~⑥のようになります。なお、引いたくじは次のくじを引く前に袋に戻すものとして考えます。
こちらも具体例①と同様に $n$ が大きくなるにつれて、サイコロの目の平均の分布は正規分布の形に近づいてく様子が見て取れます。くじを引くと、当たりくじと外れくじのどちらかが出るため、当たりくじの枚数は二項分布に従っています。二項分布に従う集団でも、サンプルの数が増えるにつれて、サンプルの平均は正規分布に近づいていきます。
ところで上記の二項分布の性質を二項分布の正規近似あるいはド・モアブル―ラプラスの定理といいます。二項分布の正規近似は中心極限定理の特殊系であり、中心極限定理を認めればすぐに証明することができます。
二項分布の正規近似の定義は以下の通りです。
$n$ は標本の数、 $p$ は特定の事象が起こる確率、 $np$ は $n$ 回標本を抽出したときに特定の事象が起こった回数を意味します。具体例②の場合、 $n$ がくじを引いた回数、 $p$ が当たりくじを引く確率、 $np$ が引いた当たりくじの枚数となります。
ここでは一様分布・二項分布の集団からサンプルを抽出した場合を例として、サンプルの数が増えるにつれて、サンプルの平均が正規分布に近づいていく様子を確認しました。もちろん一様分布・二項分布以外の分布に従う集団の場合でも同様サンプルの数が増えるにつれて、サンプルの平均が正規分布に近づいていきます。
またこのとき $p$ に着目すると以下のようにいうこともできます。
中心極限定理と大数の法則の違い
中心極限定理と混同されがちなものとして、大数の法則があります。大数の法則は、以下2種類の法則からなります。
- 大数の弱法則
平均 $\mu$ と分散 $\sigma^2$ が存在する時、任意の正数εに対して、以下の式を満たす
- 大数の強法則
平均 $\mu$ が存在する時、以下の式を満たす
厳密には両者は異なるのですが、簡単にまとめると「サンプルの数 $n$ が増えればサンプルの平均値 $\bar{X}_n$ は元の集団の平均値に近づいていく」ということを意味しています。
ここで改めて中心極限定理と大数の法則の意味を整理してみます。
- 中心極限定理
- 大数の法則
両者を比較すると、
- サンプルの平均値と元の集団の平均値が近似できることを示しているものが大数の法則
- サンプルの平均値と元の集団の平均値の差が近づいていく過程をそのばらつき(分散)とともに示しているものが中心極限定理
と考えることができます。大数の法則をさらに深堀りしたものが中心極限定理というように理解するとイメージがつきやすいと思います。
中心極限定理はなぜ有用か
中心極限定理がなぜ有用か、それはサンプルの平均値を正規分布に従うものとして考えることができるからです。このことにより、サンプルから、元の集団の平均値(真の平均値)及びそのばらつきを推定することができます。
例えば、これから日本人の平均身長を調べるとしましょう。最も正確に平均身長を測る方法は、直接日本人全員の身長を測定し、その平均値を計算することです。しかし、現実には日本人全員の身長を測定するなどといったことは不可能です。よって実際に日本人の平均身長を調査する場合、身長を測定する人をランダムに選び、その人たちの測定結果から日本人全体の平均身長を推定するという手段が取ることになります。
このとき注意すべきことは、ランダムに選んだ人の測定結果(標本)の分布が日本人全体の身長の分布とぴったり一致するわけではないということです。ランダムにサンプルを抽出するとき、サンプルのデータには確率的なばらつきが生じます。通常では、ばらついた値はどのような分布に従うかがわかりづらく、求めたい真の平均身長やその範囲を正確に把握することが難しくなります。しかし、中心極限定理のおかげで多数のサンプルを取ったうえでその平均値を求めれば、ばらついた値を正規分布という私たちが良く知る分布に落とし込むことができます。私たちは正規分布がどのようにふるまうか詳細に把握しているので、結果として値の平均値やばらつきを予測できるようになるのです。
従って、ランダムに選んだ人の平均身長を測定することで、日本人の平均身長として最も可能性が高い値、及びその値がおおよそどの範囲に収まっているか推定することができます。一般的にサンプルが十分な数であれば(多くの場合サンプル数が1000を超えていれば)、サンプルの平均値の分布は実質的に正規分布として考えることができます。サンプルの平均値が正規分布に従っていれば、真の平均値が大体どの範囲に収まっているかを推定する「区間推定」や、区間推定の考え方を応用して仮説を検証する「検定」を行うことができるのです。
例題―実生活における中心極限定理の活用
私たちの実生活で出てくる指標にも、中心極限定理の考え方が用いられているものがあります。テレビ番組の視聴率が良い例です。
視聴率には、テレビ所有世帯のうち、どのくらいの世帯でテレビが見られていたかを表す「世帯視聴率」と世帯内の4才以上家族全員の中で誰がどのくらいテレビを視聴したかを示す「個人視聴率」がありますが、本記事では「世帯視聴率」を視聴率として考えます。視聴率は専門の調査会社が集計をしていますが、テレビを保有する世帯に対して手当たり次第、番組を視聴したか調べているわけではありません。一部の世帯をサンプルとして選び、番組の視聴履歴を調べているのです。例題を見てみましょう。
例題.視聴率の区間推定
前提)
- 関東地区における視聴率調査対象世帯数は2700世帯として計算します
- 各世帯による調査への回答は、「テレビ番組を視聴したか否か」のいずれかになるため、視聴率は二項分布に従います
解法)
調査対象世帯のうち番組を視聴した割合の平均(以下標本比率)は0.346(視聴率34.6%を割合に変換)、分散は0.346 ×(1 – 0.346) = 0.226 となります(式(*)より、詳しくは具体例②を参照)。
これをもとに標本比率の平均の分布を考えます。標本比率の平均は変わらず0.346となります。標本比率の平均の分散は(標本比率の分散)÷(標本数:調査対象世帯数)なので、0.226 ÷ 2700 = 0.000084になります。ここで中心極限定理の登場です。視聴率データの標本の数が2700と十分に大きいので、同番組を視聴した割合の平均値は平均0.346、分散0.000084の正規分布に従うと考えることができます。
\[ z = \frac{p – \hat{p}}{\sqrt{\frac{p(1-p)}{n}}} \]と置くと、 $z$ は平均 0、分散 1の標準正規分布に従うと考えることができます。
このとき $p$ は標本比率、 $\hat{p}$ は母集団比率の推定量、$\sqrt{\frac{p(1-p)}{n}}$ は標本の標準偏差、$n$ はサンプルの数、$z$ は標本比率平均と母集団の比率(母比率)の平均の推定量の差を標準誤差(標本比率の標準偏差)で割った値です。
実際に同番組の視聴率の95%信頼区間を求める式は以下のようになります。
\begin{flalign*}
& z = \frac{0.346 – \hat{p}}{\frac{0.475}{\sqrt{2700}}} \quad \text{(1)} & \\
& z \text{は標準正規分布の下側2.5\%点から上側2.5\%点の区間内にあるので、} & \\
& -1.96 \leq z \leq 1.96 & \text{(2)} \\
& (1)を(2)に代入すると、-1.96 \leq \frac{0.346 – \hat{p}}{\frac{0.475}{\sqrt{2700}}} \leq 1.96 & \\
& \Rightarrow \quad 0.346 – 1.96 \times \frac{0.475}{\sqrt{2700}} \leq \hat{p} \leq 0.346 + 1.96 \times \frac{0.475}{\sqrt{2700}} & \\
& \Rightarrow \quad 0.328 \leq \hat{p} \leq 0.364 &
\end{flalign*}
よって、視聴率 $\hat{p}$ の95%信頼区間は0.328〜 0.364となります。これが意味することは、視聴率の調査を100回行ったとき、32.8%〜36.4%の範囲内に95回は真の視聴率が含まれると考えられるということです。これにより、真の視聴率のおおよその範囲を推定することができました。
まとめ
本記事では中心極限定理について、①中心極限定理とは何か、②なぜ中心極限定理が有用か、③実生活での応用例を重点的に解説しました。本記事の要点をまとめると以下のようになります。
- 中心極限定理とは以下の法則である
- 中心極限定理により、多数のサンプルデータをとったときその平均値が正規分布に従うため、確率的にどのようにばらつくのか詳細に把握することができる
- 中心極限定理により、母集団の真の平均値を推定する区間推定やそれを応用した検定を行って、実生活で起こる確率的な現象を統計的に把握することができる
中心極限定理は統計学の基礎を学ぶ上で非常に重要な概念です。本記事の内容をきちんと抑えることで、区間推定や検定などビジネスや研究で用いられる概念の理解や統計検定2級の学習に大いに役立つと思います。ご自身が中心極限定理及び周辺の統計的概念について、腹落ちするまで繰り返し学習すると統計学の理解が深まります。



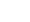


最近はChatGPTや生成AIのニューラルネットワークの基礎理論が分かりやすいと注目されている久保田邦親博士の材料物理数学再武装では、中心極限定理は等確率の原理からできているんだって。目からうろだったわ。あとブラックボックス問題なんかへの大局観をやしなえる関数接合論、経営学ではKPI競合モデルとしてビジネス関係のシナジー効果の解析にも使われているらしい。一読する価値あり。