
あなたはデータ分析の手法をいくつ言えるでしょうか?分析手法の引き出しはあればあるほど、データに対する考察の量を増やし、分析の質を高めることができます。
本記事ではこれからデータ分析に本格的に取り組む方向けに、MBAプログラムのマーケティングリサーチの授業でも紹介されている代表的な分析手法を25種ピックアップし、それぞれ解説しました。初学者でも理解できるようなるべく数式を持ちいず、イラストを多用して手法のイメージをつかんでもらえるような構成にしています。
データの分析手法は、そのカテゴリごとに記事や本が構成されていることが多いですが、この記事ではそれらを一つにまとめて紹介します。そのため本記事の分析手法を把握しておくことで、代表的な分析手法を網羅的におさえることができます。
また、データ分析そのものについては以下の記事をご参照ください。
目次
手法一覧
目的 | 手法 | キーワード |
1.データの差を統計的に比較する | ・カイ二乗検定 ・t検定 ・分散分析 | A/Bテストを統計的に行う |
2.複数のデータを要約する | ・因子分析 | 共通因子を発見する 知覚マップを作成する |
・主成分分析 | 複数の変数を合成する 知覚マップを作成する | |
・多次元尺度構成法(MDS) | 知覚マップを作成する | |
・コレスポンデンス分析 | クロス集計表を可視化する | |
・数量化Ⅲ類 | 2値データを用いたコレスポンデンス分析 | |
・補足:選好回帰分析 | 製品の属性と満足度の関係を理想ベクトル、もしくは理想点で表現する | |
3.データを分類する | ・クラスター分析 | 似た要素ごとにグループ(クラスター)にまとめる |
・潜在クラス分析 | クラスへの所属を確率的に表現する | |
4.データから予測する | ・判別分析 | 質的な変数を分類する |
・数量化Ⅱ類 | より柔軟な判別分析 | |
・決定木分析 | 木構造でデータを分類・予測する | |
・ランダムフォレスト | 複数の決定木を用いる | |
・コンジョイント分析 | 構成要素の影響度合いを把握する | |
・線形回帰分析 | データの分布に直線を引く | |
・数量化Ⅰ類 | 説明変数が質的変数の重回帰分析 | |
5-1番外編①:テキストマイニング | ・特徴語抽出 | 文章を特徴づける語を抽出する |
・共起分析 | 共起関係にある語句を調べる | |
・階層的クラスタリング | 似た文脈で用いられる語句をまとめる | |
5-2番外編②:(ID-)POSの分析 | ・ABC分析 | 売れ筋・死に筋商品を把握する |
・デシル分析 | 金額で顧客を分類する | |
・RFM分析 | 最新購買日・頻度・金額で顧客を分類する | |
・アソシエーション分析(バスケット分析) | 購買パターンを把握する |
1.データの差を統計的に比較する
この章では統計的な手法を利用して、データの差を客観的に比較し評価する手法を紹介します。
さて、データの差を客観的に比較すると何が嬉しいのでしょうか。
「先月100人の来客者が、今月は120人に増えた!」
あなたはこの結果をどのように解釈しますか?「単純に売上が伸びて良かった」、と思ってもいいのでしょうか?
たまたま今月だけ店の前を通る人の数が増えたために、たまたま売上が上がったのかもしれません。
数字を比較するときに、数字の大小だけで決めてしまう場面は多いと思います。
統計の力を借りれば、そうした主観に頼らず、客観的に判断を下すことが可能になります。
カイ二乗検定・t検定・分散分析
カイ2乗検定・t検定・分散分析は、2つもしくは2つ以上の数字の差は偶然か否か、という問いに答える分析手法です。大学で統計を学ぶ時や、統計を基礎から勉強しようとすると必ず出てくる代表的な手法です。
例えば「100と120の間にある20という差は偶然できた差か」、といった問いに答えてくれます。
これらの手法は、扱うデータによって扱われ方が異なります。その数値が購買人数のようなカウントデータならカイ二乗検定、売上や利益のような連続値ならt検定を使います。その一方、3つ以上の数字をいっぺんに見たいときは分散分析を用います。
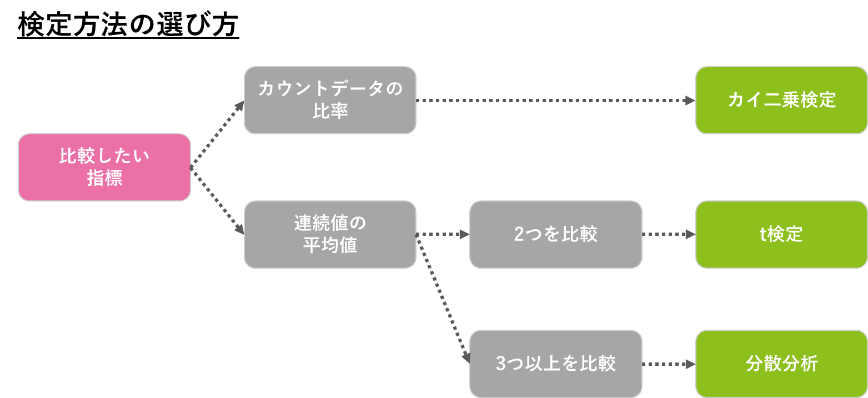
※カウントデータ:「購入した人」や「来店した人」など、1人,2人…というように一つ一つ積みあがっていくようなデータです。
※連続値:売上金額や購買数量など、平均値の算出をすることができるデータです。
この分野ではよく「検定」という言葉を目にします。検定は統計的検定もしくは仮説検定の略として使われます。簡単に言うと検定とは、「部分的に得られた数字から、全体に関して仮説を立てたとき、それが正しいかどうかを確率的に確かめる手法」です。
部分から一般化していいの?たまたまじゃないの?という問いに答える作業だとイメージすると分かりやすいかもしれません。
|①カイ二乗検定(独立性の検定)の例
ここに桃があります。この桃をもっとかわいくしたいと思ったあなたは、リボンをつけてみました。どっちがかわいいと思いますか?

アンケートをとると以下のような結果になりました。

リボンありの方が5人ほどOKの数が多いですね。しかしこの5人の増加はたまたまなのでしょうか。それともリボンのおかげで発生した、統計的に偶然とは言い切れない5人なのでしょうか。
今回は「かわいいと感じた人数」のカウントデータです。そのためこの表をもとにカイ二乗検定を行います。
検定を行うと、偶然ではないとは言い切れない、という結果になります。リボンだけ付けても、統計的に優位な変化は起こせないという結果になりました。
|②t検定(1標本問題)の例
あなたは桃の農家です。毎年平均300gを目指して桃を栽培しています。
しかし今年は「なんだかいい感じだぞ?」と思って、試しに10個収穫して重さを測ってみました。するとそれらの平均は306gになりました。

平均で見ると、例年に比べ今年の桃は少し重そうですね。
しかし、果たしてこの6gの差は必然の結果なのでしょうか。それとも偶然起きた誤差のようなものなのでしょうか。
今回の例では、桃の重さは連続値なのでt検定を用います。
検定を行うと、「平均値は300gとは言い切れない」といった結果になることが分かります。すなわち、今年の桃の重さは例年と比較して重そうだということが言えそうです。
|③分散分析の例
あなたは桃の農家です。日課である桃の木の手入れをしていると、木によって桃の成長具合が違うのではないか、と違和感を覚えました。
そこで3本の木をランダムに選んで、10個ずつ桃を収穫し、桃の重さを比較してみました。

この結果を見て、木によって桃の成長具合が異なるといえそうでしょうか?それともこれら平均値の差は誤差でしかないのでしょうか?
分散分析を用いると、これらの平均値の差は偶然ではないと言い切れない、ということが分かります。どうやらセグメンテーションの仕方を変える必要があるようです。
|適用例
この手法は主に「AとBには偶然といえない差がある、yesかnoか」という疑問に幅広く答えてくれます。そのため固定された適用の仕方はなく、様々な事象に用いることができます。例えば、以下のように使用することが考えられます。
- Webページのレイアウトに関するA/Bテスト
- 商品の製造における異常検知
- 販促キャンペーンの効果検証
2.複数のデータを要約する
この章では、データを要約する手法に関して紹介します。
データが要約されるとはどういうことでしょうか。また要約されると何が嬉しいのでしょうか。
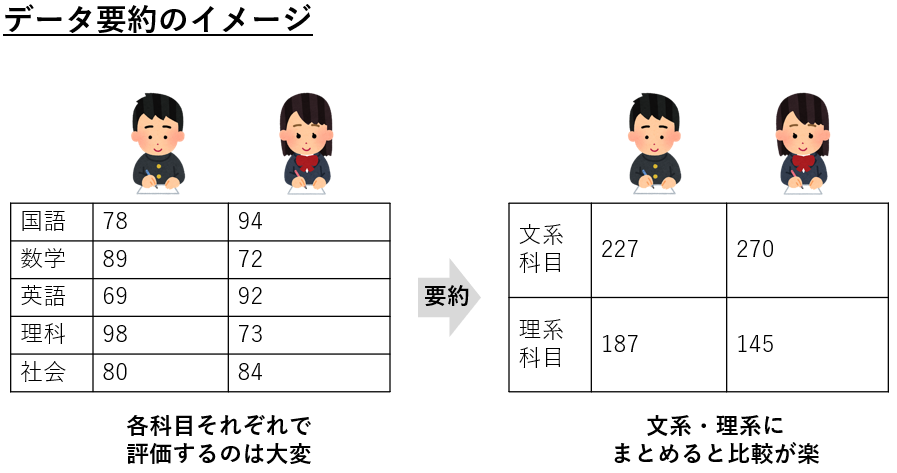
データを要約する目的は、「複雑なものを、情報量を損なわず簡単に表現する」ことだといえます。複雑なものをシンプルにしてあげることで、データ全体に関する解釈がしやすくなります。
因子分析
因子分析は、複数の変数に影響を与える隠れた要素(共通因子)を探り出す手法です。因子とは、ある結果を起こすもととなる要素のことです。そして共通因子は、複数の変数に対して共通性を持っている因子であるということができます。因子分析のイメージは、下図のピンク部分を特定するイメージです。
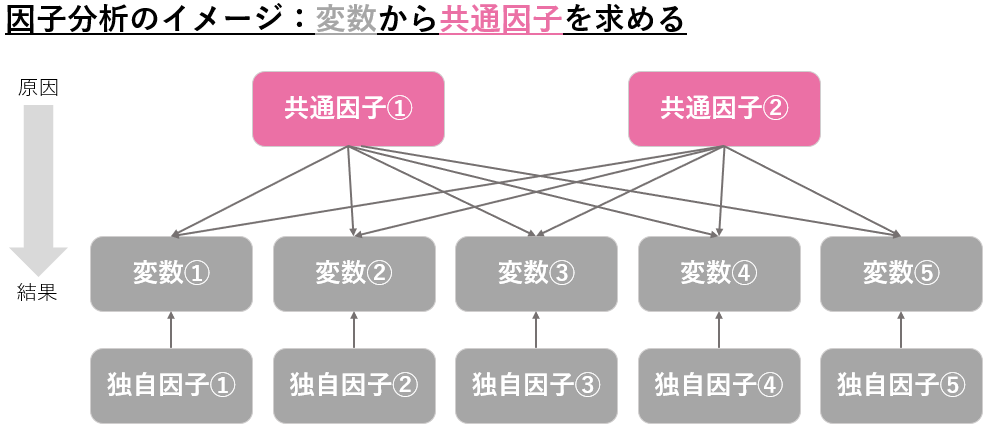
まだ難しいと思うので、例を示します。
|因子分析の例
あなたは桃Aを専門に作っている桃農家さんです。あるときスーパーに行くと、いろいろな種類の桃が置いてありました。

これを見てふと、「自分の作っている桃Aは他の桃と何が違うとお客さんに認知してもらっているのだろう?」とあなたは思いました。あなたは桃Aの甘さに自信があります。
そこでスーパーのお客さんにアンケートを取りました。

このままではどう解釈したらいいかわからないですよね。
しかし、直観的に「高い桃は甘くてジューシーで色がきれいだろうな」と思えないでしょうか?
つまり、今回のアンケート結果の背後に、桃の「高品質―リーズナブル」といった共通因子があるのではないかと考えられます。そして、これら共通因子の影響を受けて、今回のようなアンケート結果がもたらされたといえるのではないでしょうか。
ここで因子分析をして、アンケート結果に影響を与える共通因子を探ってみます。
すると例えば以下のような結果になりました。
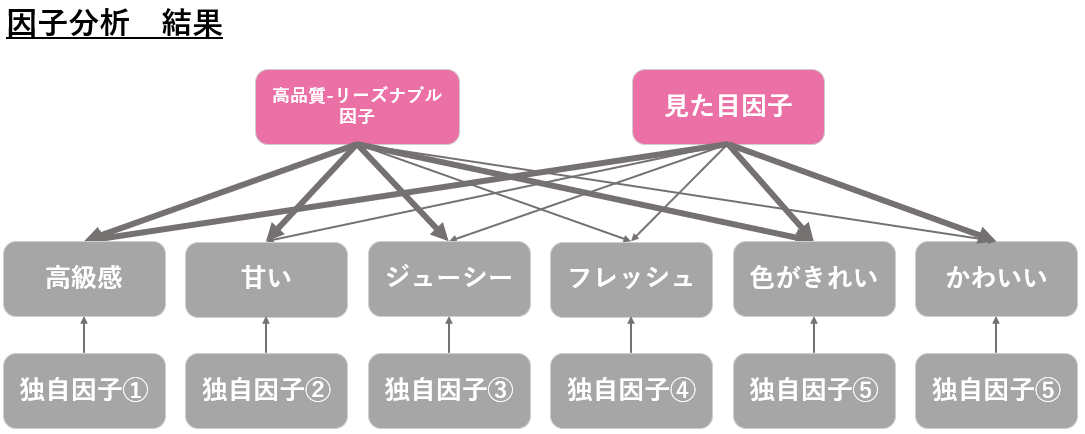
因子分析の結果、2つの共通因子が発見されました。1つが仮説にもあった「高品質―リーズナブル因子」です。そして2つ目は「見た目因子」です。新しく潜在的な因子を発見することができました。こうした直観では発見できなかった因子を発見できることも、因子分析のメリットです。
さらに、因子分析の結果は以下のようにマッピングすることもできます。

この結果から、桃Aは品質そこそこの低価格な商品として認知されていることが分かりました。
|適用例
因子分析はカテゴリやブランドのイメージを把握するためによく利用されます。そのためアンケートデータとの相性が非常に良いです。
例えば以下のような利用例が考えられます。
自社製品および競合製品に関するアンケートから、同一カテゴリ内の製品の知覚マップ(ポジショニングマップ)を作成する。
あるブランドの製品のラインナップを増やす際に、既存製品に関する知覚マップ(ポジショニングマップ)を作成し、カバーしきれていない領域を埋める製品コンセプトを考える。
主成分分析
主成分分析は、いくつかの変数を組み合わせて、少数の変数にまとめる手法です。この主成分分析も、因子分析と同様にデータを要約するのに用いられる代表的な手法です。
この変数を組み合わせることを、変数を合成するといいます。そして合成されて新しくできた変数を主成分と呼びます。下図は主成分分析のイメージ図です。ピンク部分を作り出すのが、主成分分析のゴールになります。
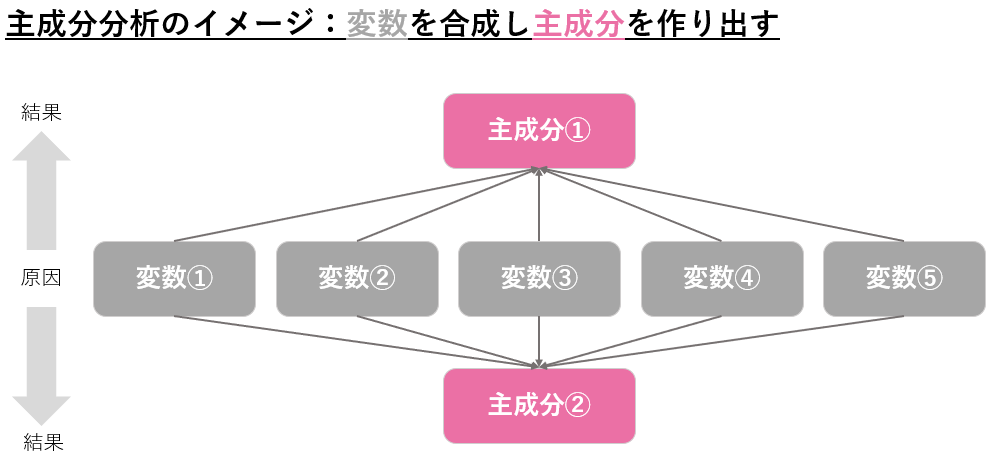
|主成分分析の例
こちらも因子分析と同じ例を用いましょう。つまり、各桃に関するアンケート結果を用います。
アンケート結果から各桃の評価を行うとき、どのように評価をすればよいでしょうか?個々の項目を見ていくのは解釈が難しそうです。
ここで主成分分析を用います。主成分分析を用いて解釈のしやすい総合指標をつくります。
主成分分析を行うと、以下のような結果になりました。
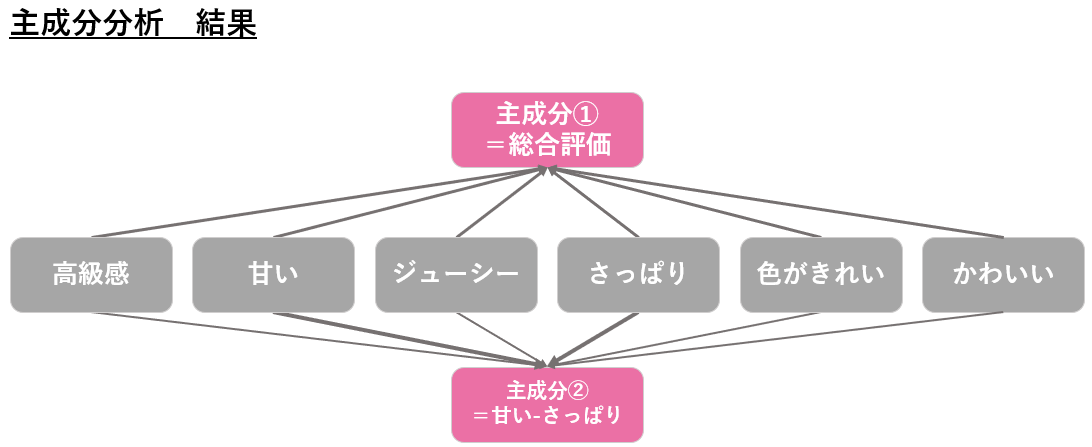
主成分分析の結果、アンケート結果が「総合評価」という主成分と「甘いーさっぱり」という主成分で表されることが分かります。6個の項目だったのが2個の指標に置き換わったので解釈が楽になったのではないでしょうか。
主成分分析も因子分析と同様に、以下のようなイメージでマッピングすることができます。
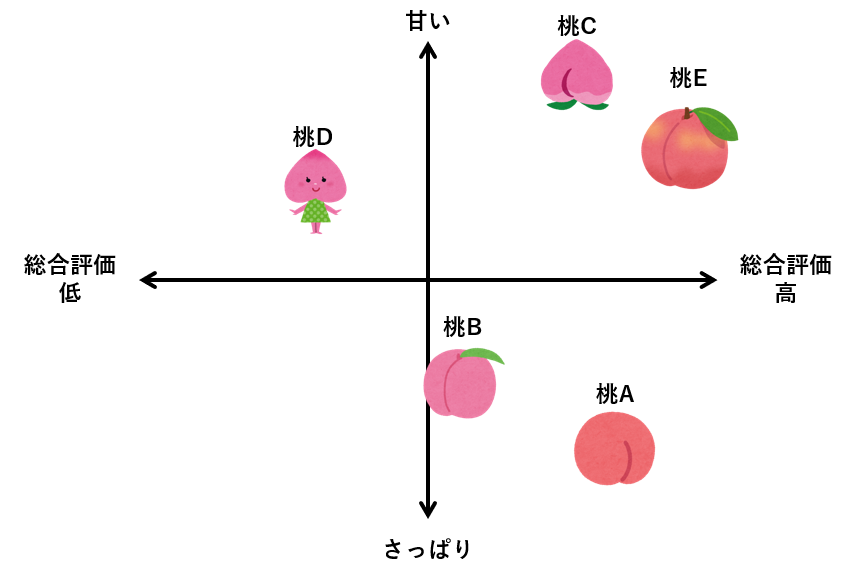
桃Aはさっぱり系に分類され評価も高いことが分かります。直接的な競合としては桃Bが考えられますが、今のところ総合的には桃Aの方が勝っているといえそうです。
ここまで見ると、主成分分析と因子分析はよく似ているように見えます。多変量のデータを要約する手法、という点では共通しています。
しかし、因子分析は共通因子がデータの背後にあると仮定して、その共通因子を探りに行きます。これに対し、主成分分析は今あるデータから新しい主成分を作る手法です。つまり、データの因果関係の矢印が逆になります。
さらにかみ砕きます。
北海道が地元のカップルのAさんとBさんがいるとします。因子分析は変数の共通因子を探る分析です。この例では「北海道民」がこの2人の共通因子といえます。その一方主成分分析は変数を合成して主成分を作る分析です。2人が付き合った「カップル」というカテゴリが主成分だといえます。
|適用例
主成分分析もデータの要約という観点から、因子分析と同様の使い方をすることができます。またほかにも異常検知や機械学習の文脈でも使用されることがあります。使用例としては以下が挙げられます。
アンケート調査による知覚マップ(プロダクトマップ)の作成をし、競合との相対的な自社製品のポジションを把握する
正常を表す主成分を作り出して異常検知の基準にする
機械学習における次元圧縮
多次元尺度構成法(MDS)
MDSは、知覚マップを作成するのに用いられます。似たもの同士をまとめてくれるイメージです。
「多次元」とありますが、2次元で表されることの方が多いです。なぜなら立体以上より平面の方が解釈しやすいからです。
MDSも因子分析に似ています。どちらでも知覚マップを作れるという点では共通しています。しかし、両者は扱うデータが異なります。
因子分析では複数種類の質問項目から類似性を探りますが、MDSは類似度を直接聞いたデータを用います。

|MDSの例
あなたは桃Aを専門に作っている桃農家さんです。あるときスーパーに行くと、いろいろな種類の桃が置いてありました。

桃の専門家のあなたからしたら、これらの桃はどれも明らかに違うように思えます。
しかし、桃に詳しくないお客さんは違いを見分けられないかもしれません。
そこで、桃ごとに他の桃とどれだけ似ているかを聞いたアンケートを作成しました。

このアンケートから得られたデータからMDSを行いました。
すると以下のようなマップを作成することができました。

MDSによって作成されるマップの軸自体は意味を持ちません。類似度が高いものが近くにプロットされているだけです。
このマップからだと、桃Aは桃Eと似ていると認知されているようです。また桃Dはどの桃とも似ていないと思われているようです。
|適用例
MDSは直接類似度を聞いたデータ用いるので、解釈はしやすい手法だと思います。しかし使用データの応用範囲が狭く、実務での使用に向いているとは言い難いです。
この手法を使用するとしたら、知覚マップ(プロダクトマップ)を作成して自社製品のポジショニングを確認する方法が考えられます。
コレスポンデンス分析
コレスポンデンス分析は、クロス集計表を視覚的に表現できる手法です。傾向の近い項目を近くに配置したマップを作成してくれます。イメージは以下のようになります。
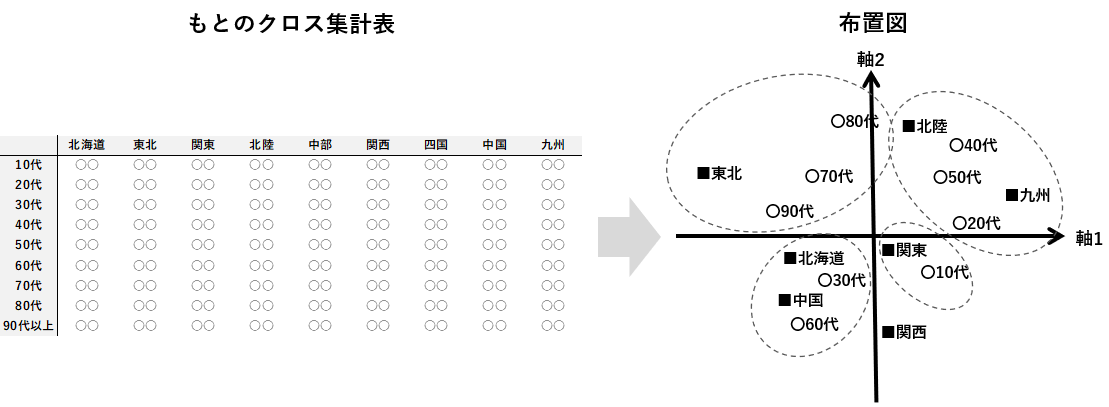
|コレスポンデンス分析の例
年代によって、桃の好みはあるのでしょうか?
直観的にはありそうな気がします。若者は甘さに酔った味が好みで、年配の方はさっぱりした味の方が好みなように思われます。
この疑問に答えるべく、あなたは各年代の人に最も好きな桃の種類を尋ねました。
その結果は以下のクロス集計表に表されます。さらに更にコレスポンデンス分析を行うと、右下図のように表せられました。
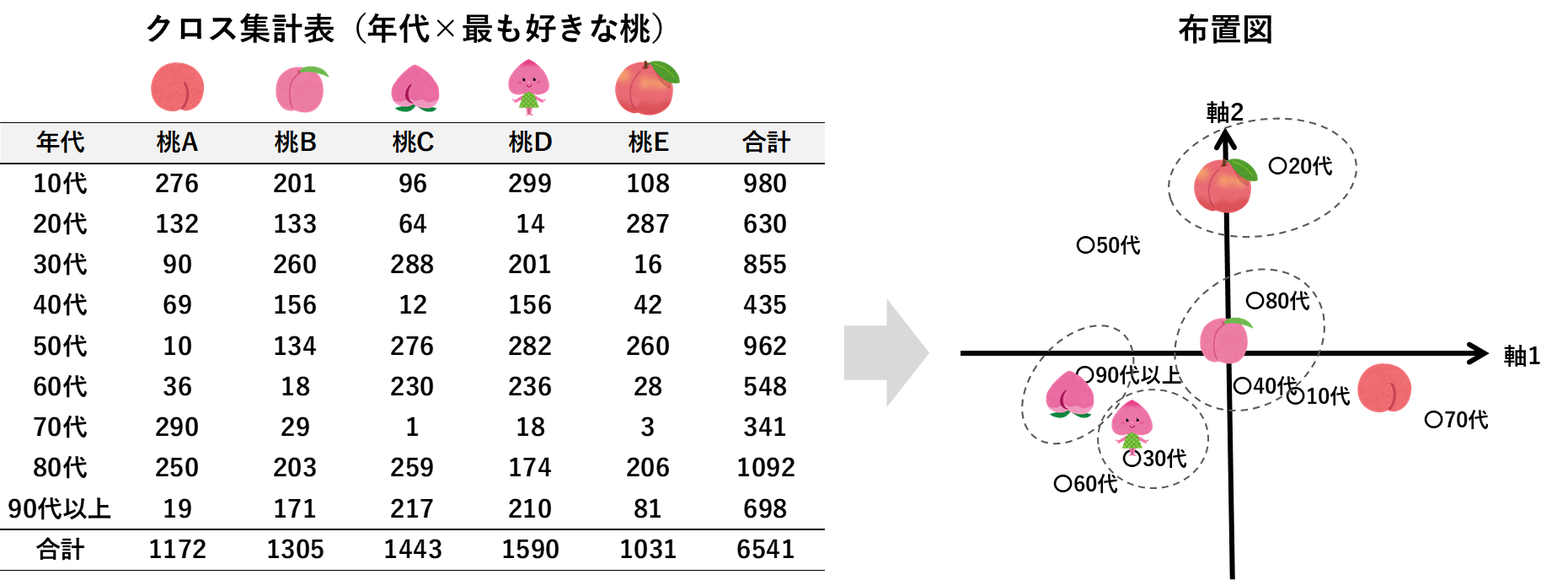
図を見ると、桃Bは比較的高めの年齢層にフィットした製品であるといえそうです。その一方で、若者は桃Eに関心を寄せているとみることもできました。
コレスポンデンス分析もまた、主成分分析などと似ているように思えます。しかし、これらは用いるデータが異なります。
因子分析や主成分分析は量的データ(点数や売上など)を用いるのに対し、コレスポンデンス分析は質的データ(非常に満足、満足、不満足が何人いるか、など)を用います。そのため、コレスポンデンス分析はアンケートデータに対して利用されやすいです。
|適用例
コレスポンデンス分析は質的データのクロス集計表を可視化するものだと述べました。そのため、例えば以下のような目的を持ったアンケートデータを分析することができます。
アンケートデータから生年代別の好きなブランドの傾向を調べる
アンケートデータから、よく使う媒体と製品の認知度の相関を調べる
数量化Ⅲ類
数量化Ⅲ類は数理的にコレスポンデンス分析と同様です。数量化Ⅲ類を用いることで項目間の相関関係をマップ可視化することができます。ただしコレスポンデンス分析と数量化Ⅲ類では、想定されているデータが異なります。コレスポンデンス分析は2×2のクロス集計表から似通った項目を見つけます。それに対し数量化Ⅲ類は、変数が質的データのローデータを扱います。そのためデータ型によって使い分けることができます。
補足:選好回帰分析
選好回帰分析は、因子分析等で得られた知覚マップから、回帰分析を用いて製品属性と顧客満足の関係を求める手法です。
因子分析では各ブランドがどの属性を持っているかを把握することができます。しかし知覚マップを作成する最終的な目標は、「なぜ、どのような要因によって、その製品が顧客によって選択されているのか」を明らかにすることです。選好分析を用いることで、製品の属性と満足度の関係を理想ベクトル、もしくは理想点で表現することができます。
|選好回帰分析の例
以下の図は因子分析で用いた知覚マップの例です。このマップの矢印が理想ベクトルであり、この矢印に沿って原点から離れるほど、高い満足度が得られるという解釈をすることができます。
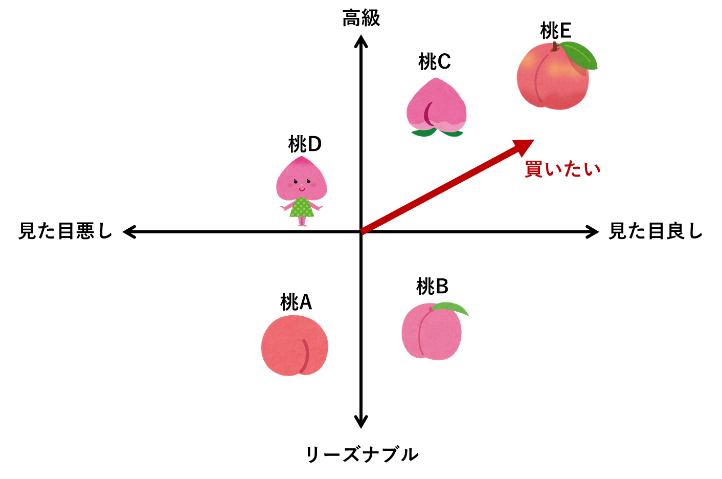
今回の場合、少し高くても見た目が良い桃を販売することで満足度が向上すると考えることができます。
|適用例
行ってしまえば線形の回帰分析をしているのと同様です。使用する場面は、因子分析等をして知覚マップを作成したときといえます。
3.データを分類する
この章では、データをいくつかのグループに分類する手法を紹介します。
ビジネスシーンにおけるデータの分類は主に、セグメンテーションに用いられます。
限られた経営資源の中から多くの売上を上げるには、自社の戦略に沿ったターゲットに的確にアプローチをする必要があります。そのようなターゲットを把握するために、性別や年齢、購買行動のパターンの違いにより、規定された市場における顧客を分割します(セグメンテーション)。このセグメンテーションには、どのような尺度・基準を用いるべきかといった点に明確な基準がありません。かといって、消費者のニーズを把握せずに直観的な基準でセグメンテーションを自動的に行うべきではありません。場面に応じて適切な分け方をしてあげる必要があります。
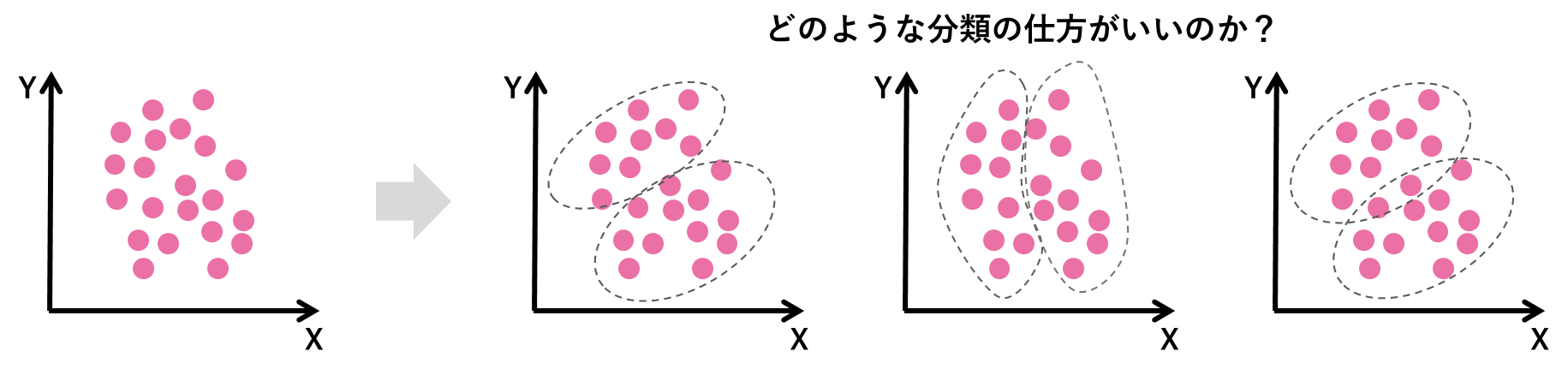
こうしたセグメンテーションを行う分析手法には、いくつかの手法が存在します。ここではクラスター分析と潜在クラス分析という手法を紹介します。
またデータの分類は必ずしも顧客分類だけに限る必要はありません。製品や地域の分類にも用いることができます。
クラスター分析
クラスター分析は、データの集合を似た者同士のグループ(クラスター)に分類する手法です。この分析はマーケティングにおいて、セグメンテーションを行うために最もよく用いられます。
クラスター分析の計算後の出力の形式は大きく2つに分けられます。1つが階層的クラスタリングで、もう一方は非階層的クラスタスタリングです。
階層?非階層?言葉ではよくわからないと思います。出力例を見てみましょう。
|階層的クラスタリング
階層的手法を用いるとトーナメント表のようにクラスターが形成されていく様子を見ることができます。階層というのは、トーナメントの分岐のことを指します。階層が深いほど、多数に分類されていることが分かります。
そして、似ているものは近くの階層に、似ていないものは遠くの階層に配置されます。
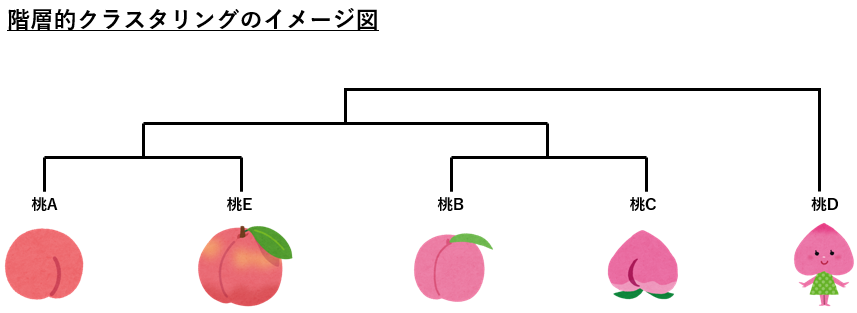
|非階層的クラスタリング(k-means)
非階層的手法を用いると、自分で指定した数のクラスターに全体を一気に分割します。ここにはトーナメント表のような階層はないので「非階層」と呼ばれます。
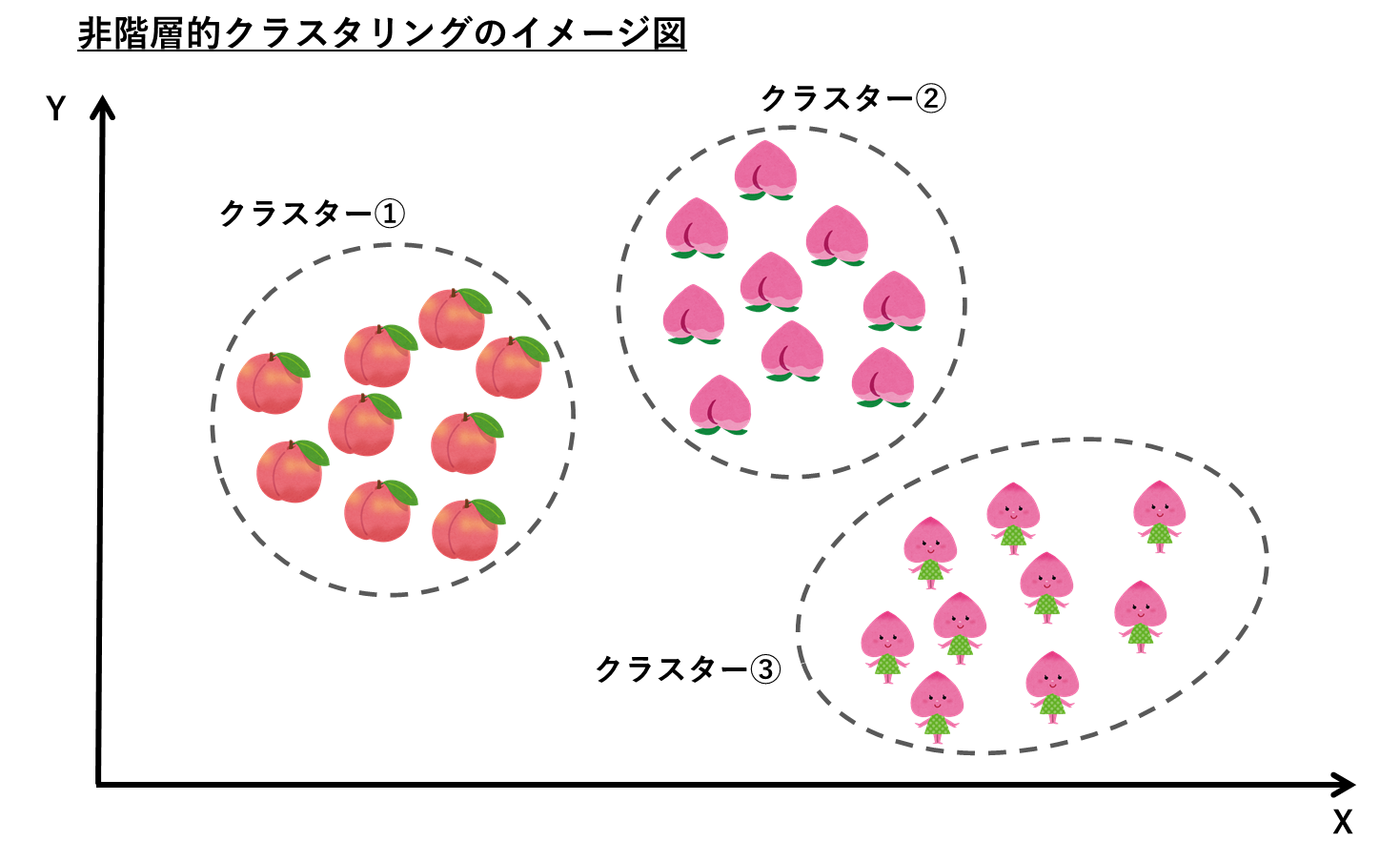
今回はk-means法という手法で分類を行いました。このk-means法は分類のルールに関する1手法です。非階層クラスタリングをするにおいて代表的な分類方法です。
|適用例
クラスター分析の代表的な利用方法は顧客分類(セグメンテーション)や製品分類です。
例えば、以下のような利用方法・活用が考えられます。
売上と利益ベースで製品カテゴリをクラスタリングし、売上はあるものの割引等で利益が出ていない製品カテゴリを特定し、過度な割引を避けるように営業店に働きかける。
会員情報(性別・年代・地域・購買履歴など)をもとにクラスター分析を行い、会員顧客の嗜好性を特定し、それぞれの嗜好に合わせたDMやイベントの招待を行う。
潜在クラス分析
潜在クラス分析もクラスター分析と同様に、セグメンテーションのためによく利用されます。しかしクラスター分析とはアプローチがやや異なります。潜在クラス分析に関しては、以下の点が代表的な特徴になります。
- 統計的情報から最適なクラス数を判断することができる。
- 分析対象のクラスへの振り分けを、各クラスに属する確率で表現する。
- 量的変数と質的変数だけでなく順序変数(ランキングなど)を使用してクラスを使用でき、分析の柔軟性が高い。
いまいちイメージつきにくいかと思うので、例を見てイメージをつかみましょう。
|潜在クラス分析の例
ここでは潜在クラス分析を用いて顧客の分類を行います。
今回の分類は、4ブランドの桃の購買履歴をもとにして行います。いくつのクラスに分類されるかも、分析の経過の中で適切な数が算出されます。
潜在クラス分析の結果、以下のように顧客が分類されると分かりました。
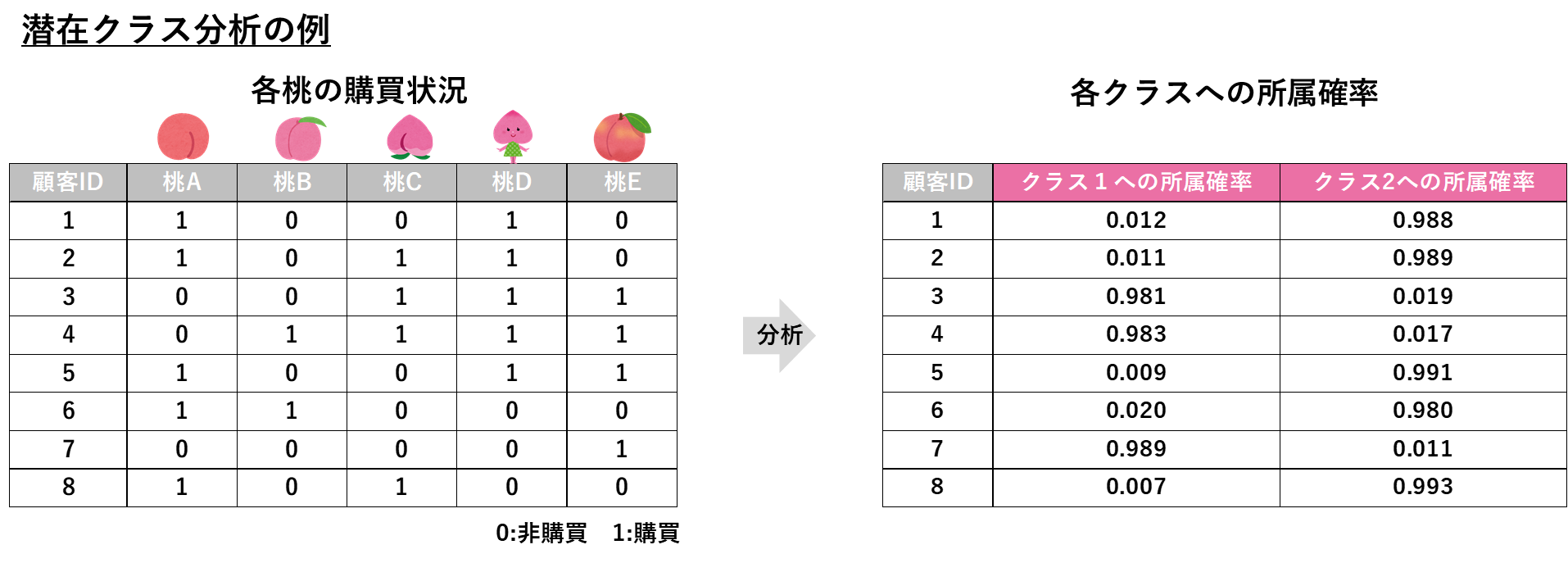
結果を見るとクラスター分析と異なり、「所属確率」という形で分類がなされていることが分かります。
この結果から、クラス1に所属する顧客は桃C、D、Eを買いやすく、クラス2に所属する顧客は桃A、Bを買いやすいということが分かります。
|適用例
潜在クラス分析も、クラスター分析と同様な利用方法ができます。潜在クラス分析は所属確率でグループが表現される点から、対象の「共通する性質」を発見することに重きが置かれています。
POSデータの購買履歴やアンケートのデータから、顧客をセグメンテーションしたり、商品に関するアンケートから商品のグルーピングに用いることができます。
4.データから予測する
この章ではデータを予測するための様々な手法を紹介します。
「データ分析をする」と聞くと、この予測がよく頭に浮かんできそうです。
データの予測はどのように行われるのでしょうか?
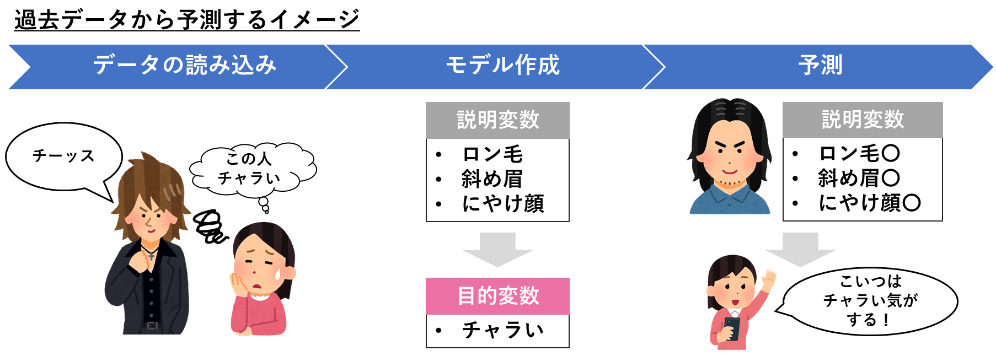
一般的な説明では「過去の説明変数と目的変数を利用してモデルを作り上げ、そのモデルから将来の目的変数を予測する」ことが予測に関するデータ分析の手順です。
よくわからない…?
それでは日常生活に置き換えてイメージしてみましょう。
私たち人間も日常生活の中でたくさんの予測を行っています。たとえば初めて会う人の印象も、私たちがその人の身なりから予測した結果です。過去の経験から、その人の内面を予測しますよね?
判別分析
判別分析は、様々な連続的な属性データ(来店回数、売上高など)から質的な目的変数(購買経験のある/なし、など)の分類を判別する手法です。判別分析では判別関数、および判別関数から計算される判別スコアによって、対象を区別します。言い換えると、判別分析は「A(ある)とB(なし)を最もうまく分けるような直線(判別関数)を引く」ことが大まかなイメージです。
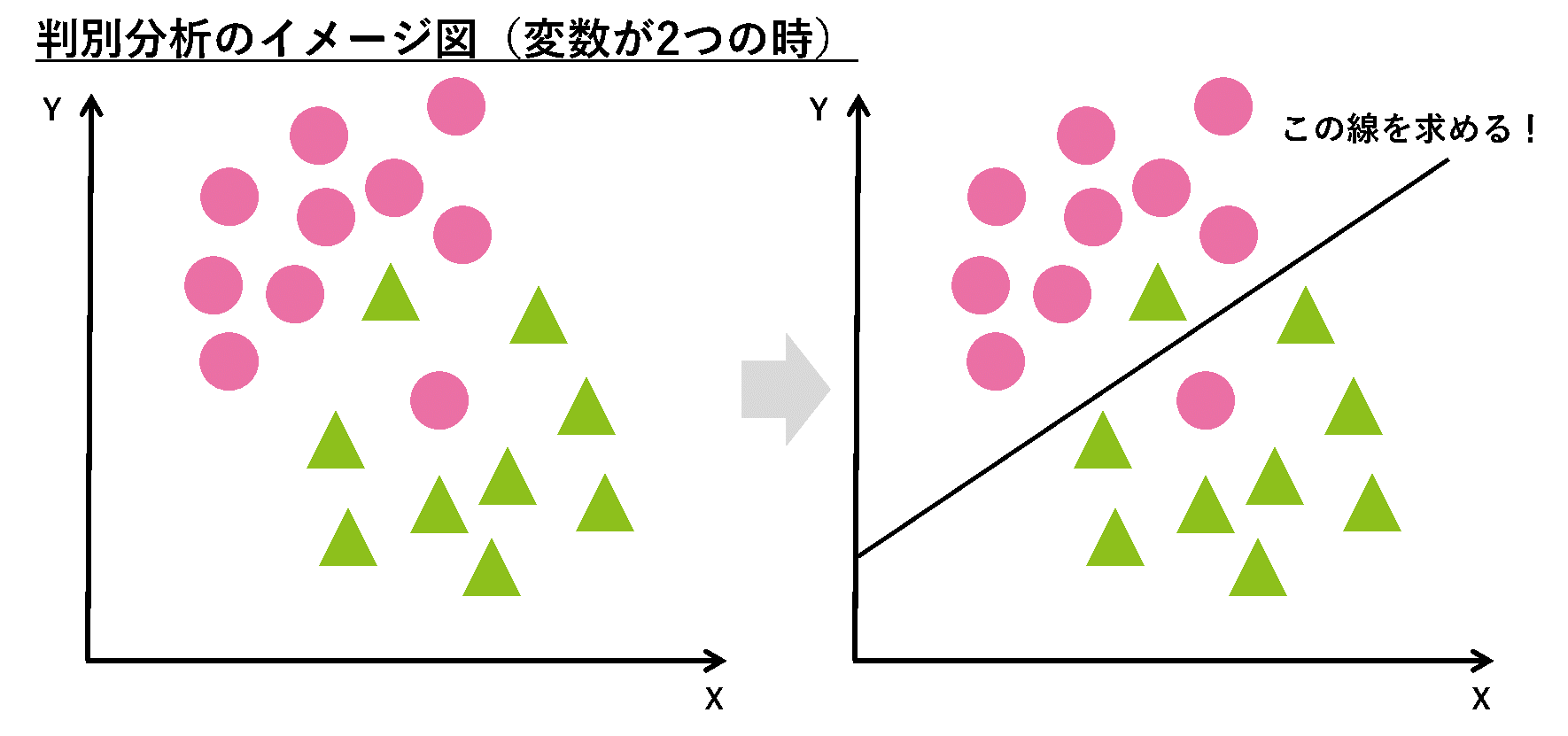
|判別分析の例
桃を買おうとしたとき、どの桃が甘いか見分けられますか?筆者は見分けられません。
では、甘い桃を見分ける状況を考えてみましょう。
甘い桃を見分ける指標として、
- 白い斑点が多いと甘い
- 産毛が多い
といったものがあるそうです。この2つの指標から桃の甘い/甘くないを予測してみましょう。
まず何回か桃を買って、白い斑点の数、産毛の量と桃の甘い/甘くないを調べました。

得られたデータから、判別分析を行います。すると以下のような式が得られます。

得られた判別式から、ID100の桃が甘いかを予測することができます。
今回は判別関数を予測のために使用しましたが、係数を標準化することで、式を構成する係数を比較して、項目間の判別への影響度を測ることも可能になります。
今回は係数の比較はできません。なぜなら斑点の数と産毛の本数は、そもそも単位が違うので直接比べられないからです。標準化はこうした単位の違いをカバーしてくれる機能を持ちます。
|適用例
上でも述べましたが、判別分析は①新規データの判別(グループの予測)、②項目ごとの判別への影響度の測定、の2点の役割を担うことができます。そのため適用例は以下が考えられます。
新規顧客に対し判別分析を行い、解約しそうな顧客かどうか予測する
製品に対するアンケートを用いて、製品のコア・イメージに大きく影響を与えている項目を特定する。
クラスター分析との併用。クラスター分析による分類を目的変数として直線を作成することで、どの項目がクラスターの形成に寄与していたか推定する。
数量化Ⅱ類
数量化Ⅱ類は、判別分析に非常に似ています。異なる点は、判別分析は目的変数と説明変数にそれぞれ質的データと量的データを用いるのに対し、数量化Ⅱ類では目的変数と説明変数の両方に質的データを用いる点です。
例えば製品の満足度に関するアンケートを用いて、高い満足度を感じる顧客を予測したり、満足度につながった要因を分析することができます。
決定木分析
決定木分析は、一定の閾値を基準とした分岐をつくり、データを分類していく手法です。まるで木のような形で結果を視覚的に見られる点が特徴です。
ただ木といってもよくわからないですよね。以下が決定木のイメージです。
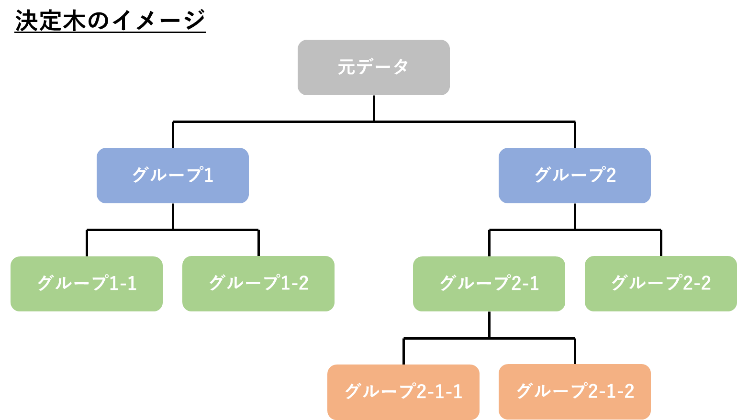
最も良く分類できそうな基準が1番上に配置されます。その基準によって分類されたデータは、また次に最も良く分類される基準に従って分類されます。これを再帰的に繰り返します。
決定木は分類と予測の両方に使うことができます。この記事では、分類の例を紹介します。
|決定木の例
あなたは桃農家です。もっとたくさんの人に桃狩りに来てもらいたいと思って広告を打つことにしました。しかし、どのようなユーザーに打てばいいかわからないです。
幸い、毎回来客者に満足度に関するアンケートを顧客属性も含めてとっていたので、この顧客の属性から、満足度が高くなりやすい顧客を広告のターゲットとすることに決めました。
決定木を用いて分析したところ、以下のようになりました。

今回の結果だと、40歳以上の男性が広告のターゲットとして適しそうです。日々の仕事から解放されたからでしょうか。
単体の決定木に依存して分析を行う際には注意が必要です。結果の可読性という点は優れているのですが、分類や予測の精度が高くなり辛く、過学習を起こしやすいからです。
決定木分析ライクに精度良く分類や予測を行う場合は、以下で説明するランダムフォレストという手法を用いることが多いです。
ランダムフォレスト
ランダムフォレストは機械学習の手法の一つで、決定木を複数用意して分析を行い、その中の多数決で結果を得る方法です。木を集めると森(フォレスト)になるイメージです。3人寄れば文殊の知恵ですね。
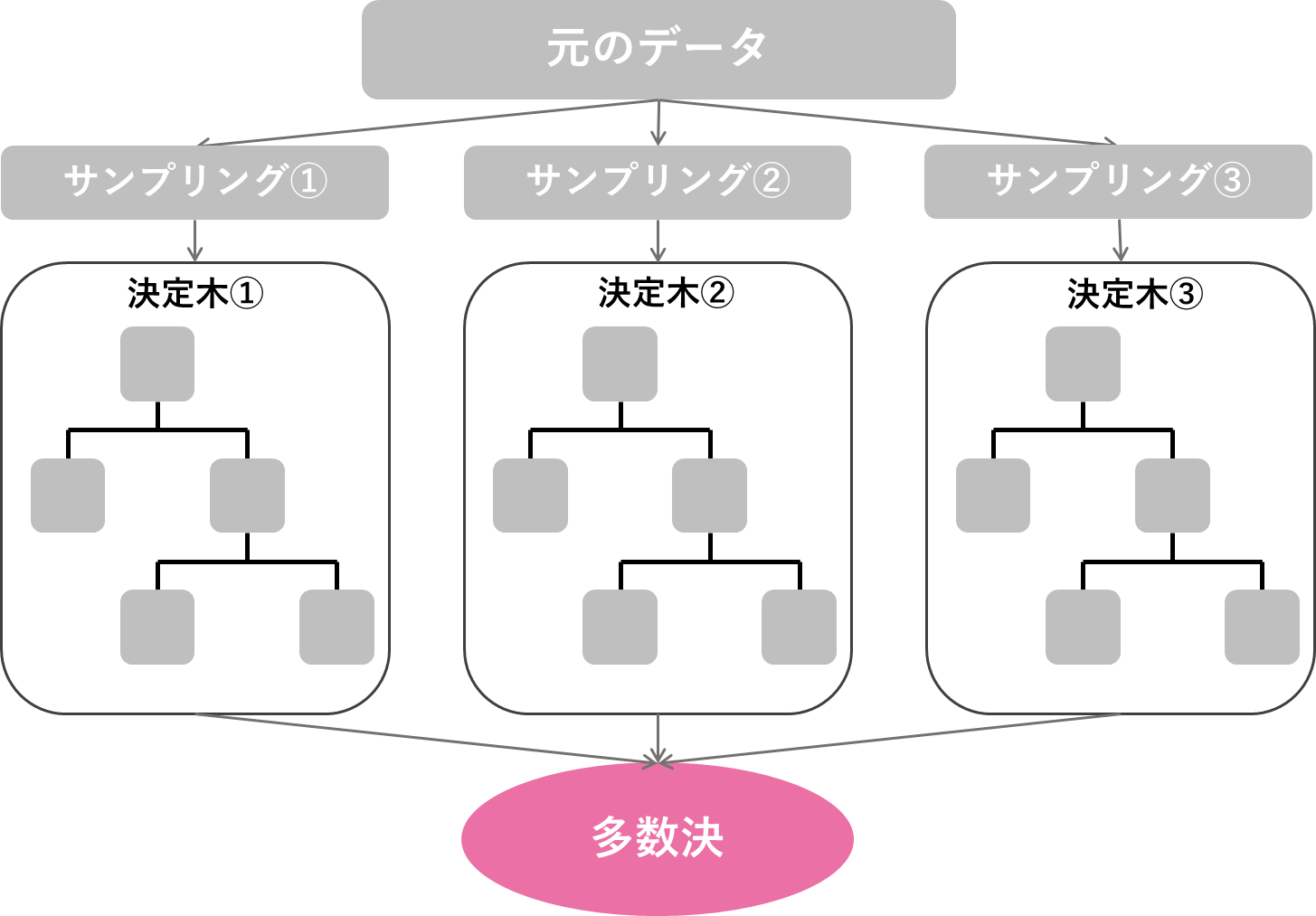
サンプリングが複数あるのが気になりますでしょうか?
それぞれの決定木の作成に対してサンプリングを行う理由は、同じデータからは同じ決定木しか生まれないからです。すべて同じような決定木になってしまったら、各決定木の出す結果も当然一緒になってしまいます。サンプリングを行うことで、異なるデータをもとに決定木を作成することができます。
|適用例
ランダムフォレストは、予測モデルを作成するときの最有力候補の一つだといえます。様々な対象に用いることができるため、使用方法は無限大ですが、いくつか例をここにあげます。
- 顧客の属性データ・購買データから離反可能性の高い顧客を特定する
- 在庫予測
- 来店者数予測
- 不良品発生予測
コンジョイント分析
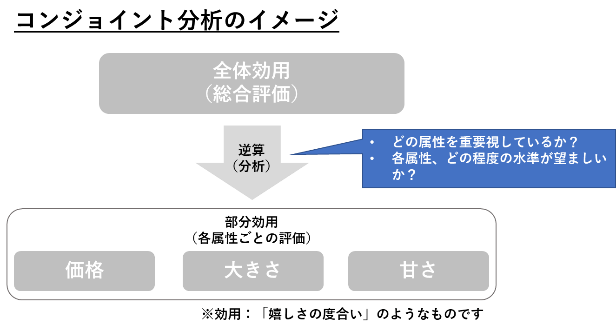
コンジョイント分析は、その商品が持つ各属性に関して消費者が商品を購入する際に優先する(妥協する)度合いを測定する分析手法です。
属性とは、例えば価格や性能といったものです。壊れやすく粗悪なものでもとにかく安さを優先するときや、その一方で少しお金を出してでもいいものを買いたいと思ったことはないでしょうか。これが商品の持つ属性を優先(妥協)するという現象です。コンジョイント分析を用いると、その各属性の優先順位および属性の最適な組み合わせを得ることができます。
|コンジョイント分析の例
あなたは桃農家です。新しい種類の桃を販売してみたいと思うものの、どのようなコンセプトの桃を売るべきか悩んでいます。アイデアとしては次のようなものを考えています。

次に、お客さんにこうした桃のプロファイルを買いたい順に並べ替えてもらいます。コンジョイント分析では、このプロファイルの並び順は、お客さんの幸せ度(効用)によって決まっていると考えます。
こうして得られたデータにコンジョイント分析を行うと、以下のような結果が出てきます。
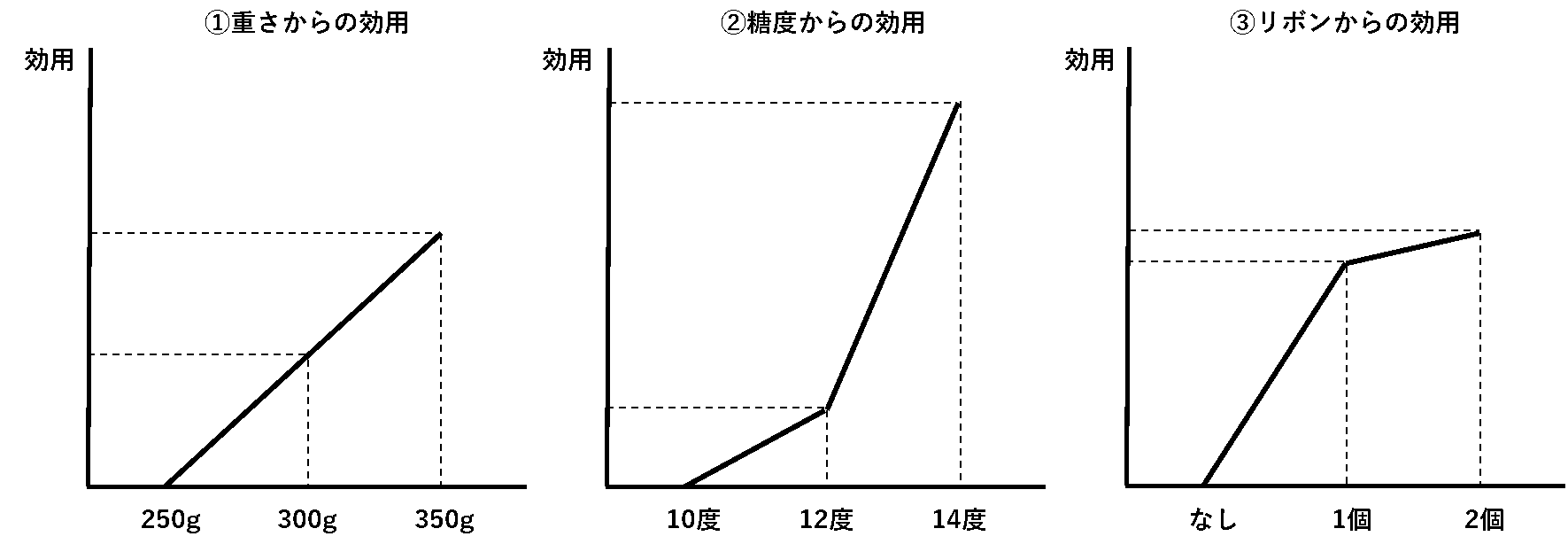
この結果を見ると、例えば桃の糖度は同じ2度上げるのでも、顧客にとっては12度から14度に上げる方が嬉しいといえます。その一方でリボンの数は、1つ付ける分にはそれなりに喜ばれるが、2つ目を付けてもあまり意味がないということが分かります。かけられるコストが限られている以上、リボンは2つも付ける必要がない、という判断をすることができます。
|適用例
コンジョイント分析は、製品・サービスのコンセプト評価を行うときに有用な手法です。特に、費用が大きすぎるためテストをすることができないような製品のコンセプトの良し悪しを決めるときによく用いられます。例えば、以下の使用法が考えられます。
新型車種に付け加える新機能や車の色を選定するとき
賃貸物件を立てる際に、その建物の種類(和風・コンクリート・ログハウスなど)、駅からの距離、駐車場の有無などの条件と、価格をどのように組み合わせるかを考えるとき
線形回帰分析(単回帰・重回帰)
線形回帰分析は、データ分析手法の中でも最も伝統的で基本となる手法です。一般的に回帰分析は、ある変数yの変動を、別の変数xを用いて説明や予測を行うために使用されます。変数xが1つだけなら単回帰分析、変数xが2種類以上あるときに重回帰分析といいます。
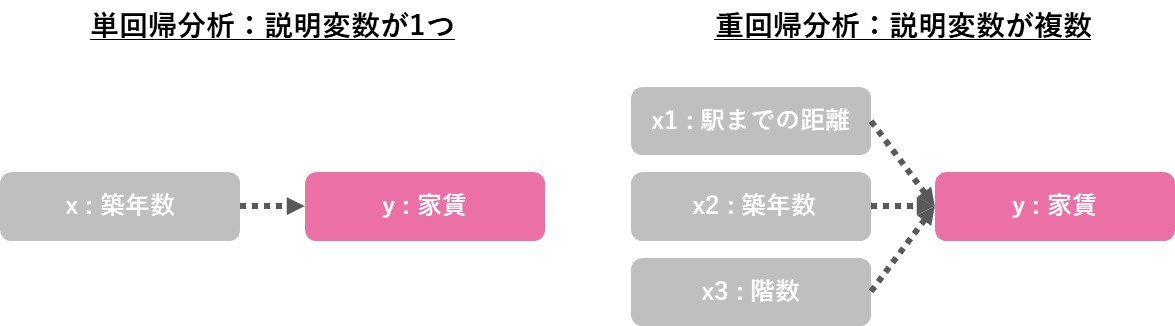
「変数」や「回帰」といった難しい言葉を使わずに表現をすると、「他方のデータを用いて、一方のデータを予測する数式を推定すること」が回帰分析の本質であるといえます。例えば家賃を予測したいときに、家賃以外の情報を利用して家賃を予測するとしたら、以下のような重回帰式が立てられます。

上で単回帰・重回帰を紹介しましたが、このうち重回帰分析の例を説明したいと思います。単回帰分析はシンプルさゆえに精度が高くなりにくく、実務で用いられることが少ないため、ここでは説明を省略します。
|重回帰分析の例
あなたは桃農家で、直売所にも桃を卸しています。桃の運搬は自分でやらなければならないので、できれば必要最低限の量だけを持っていきたいと考えています。
そこで、今までの販売履歴をもとに翌日の販売個数を予測して、持っていくべき桃の個数を決めようと心に決めました。
使う架空のデータは、①日次の販売履歴、②その日の気温、③平日/休日・祝日、の3つの情報です。

重回帰分析によって得られた予測式より、8月1日の販売個数を予測してみます。
天気予報によると、8月1日の気温は31度です。また8月1日は平日です。
従って予測される販売個数は、20+1.3×31+10×0=50個、だということが分かりました。
|適用例
単回帰分析を実務で見かけることはほとんどないものの、重回帰分析はあらゆる場面で使用されています。重回帰分では、分析の際に算出される式を用いて①予測と②要因分析をすることができます。
予測は例の通りです。得られた予測式にデータを代入し、予測したい数量を算出します。
要因分析は、予測式の係数に注目します。先ほどの例では、休日になると販売数量が10個も増えることが分かります。このことから、休日は平日よりもよく売れる、といった考察をすることができるようになります。
ただし今回紹介した重回帰分析は、連続量(売上や来客数など)の予測のみに適用できます。
例えば2値データ(「解約の有無」、「購買の有無」といったようなyes/noで表される)を予測したい場合はロジスティック回帰と呼ばれるものを使用します。
この点を踏まえて、重回帰分析は次のようなことに使用することができます。
昨年や前日の来客数および気象データを利用して、翌日の販売数量を予測し、在庫の必要数を計算する。
従業員の属性および活動データから営業成績を予測する式を作成し、営業成績と相関する要素を特定する。
仕入れ商品の価格変動を予測し、たかづかみするのを回避する。
数量化Ⅰ類
数量化Ⅰ類は、説明変数が質的変数である重回帰分析のことです。購買の有無や性別などの数値でないデータから、購入数量や来店回数などの数量を予測することができます。
5-1 番外編①:テキストマイニング
テキストマイニングは、自然言語で書かれた文章を統計的に分析する手法です。コールセンターの問い合わせ内容やチャットボットに入力された内容、顧客アンケートの自由記述欄、といったデータに対してテキストマイニングは価値を発揮します。
売上や販売数量と違い、文章で書かれた情報を読み取るのは定性的で、一筋縄ではいきません。データ量が増えれば増えるほど、すべての文章に目を通すことは物理的に不可能になります。
こうした文章を読み取る労力を補ってくれるのが、テキストマイニングの大きな価値になります。

テキストマイニングでは形態素解析という手法を用いて、文章から単語を抽出し、もっともらしい単語の列へと分解します。こうして分解・抽出された語句をもとに、単語の出現頻度・共起などが分かります。
抽出?もっともらしい?共起?言葉だけでは難しいですよね。
安心してください。テキストマイニングの代表的な手法を3つ、例を用いて紹介します。
特徴語抽出
特徴語抽出は、文章の内容を特徴づける語句(特徴語)を抽出する手法です。この特徴語は単に出現頻度で決まっているわけではなく、一般的な文章と比べて出現頻度が多いと重要だとみなすという方針のもと決定されています(そうでないと「です・ます」などは常に抽出されてしまいます)。抽出された特徴語はワードクラウドと呼ばれる形式で、人の目にもわかりやすく表現されることが多いです。
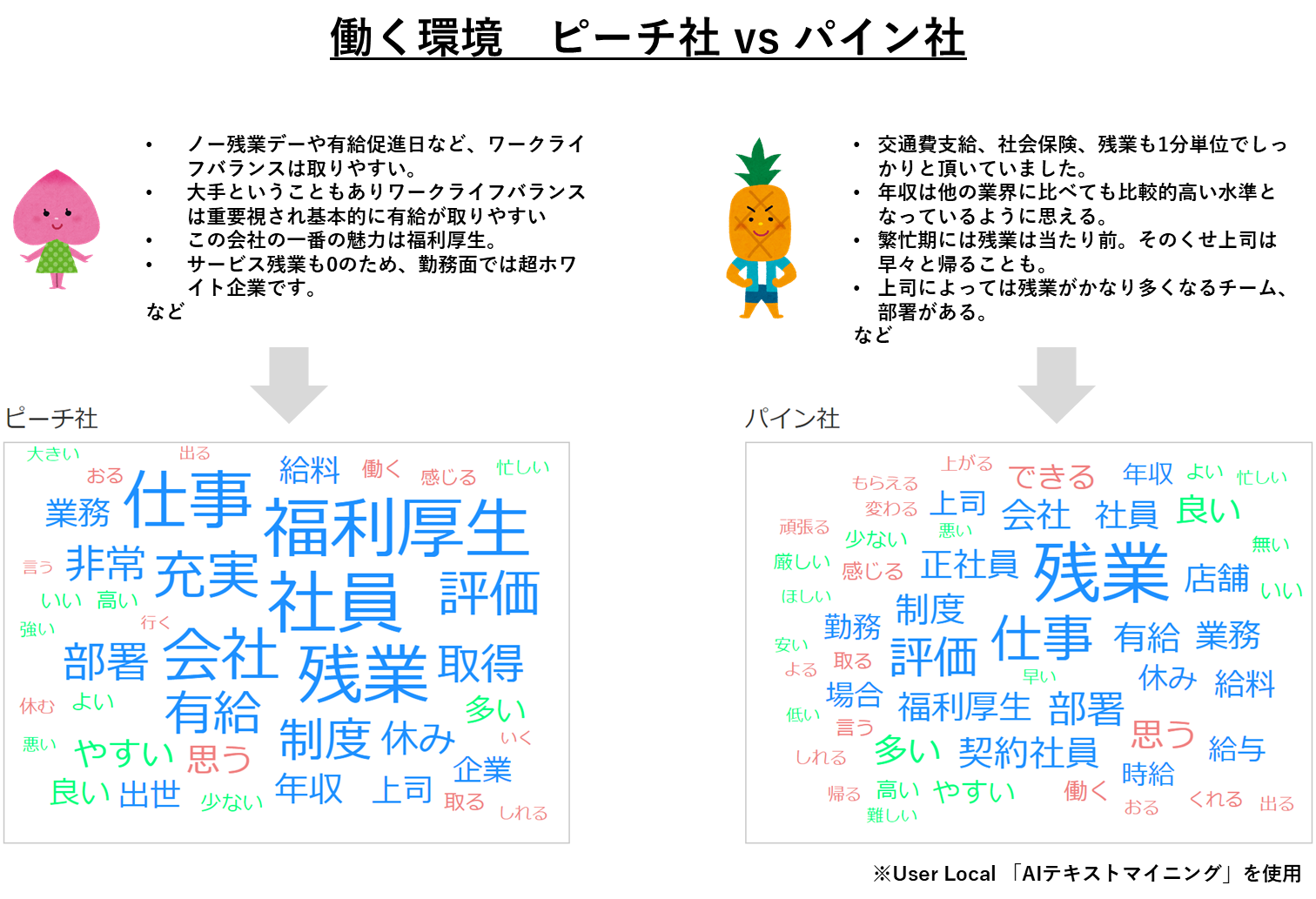
共起分析
共起分析は、「キムタク」→「かっこいい」のように共起関係にある語句を調べる手法です。共起分析をすることで、例えば自社ブランドがどのようなイメージを持たれているかを定量的に分析することができます。共起分析は共起ネットワークを用いることで文章全体の語句の共起関係を把握することができます。
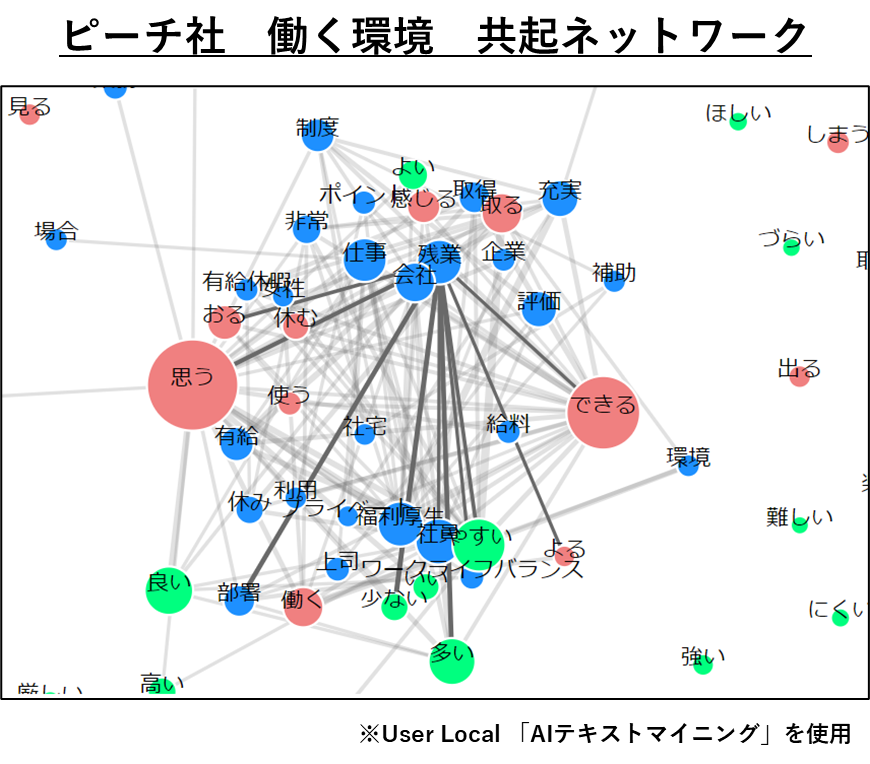
階層的クラスタリング
テキストマイニングにおける階層的クラスタリングのイメージは、クラスター分析の節で解説した階層的クラスタリングのイメージと同じです。テキストマイニングにおけるクラスタリングは、比較的似た文脈で用いられる語句同士をまとめ、一つのクラスター(グループ)を形成していきます。「階層的」クラスタリングの場合はトーナメント表のようにクラスターが形成されていきます。
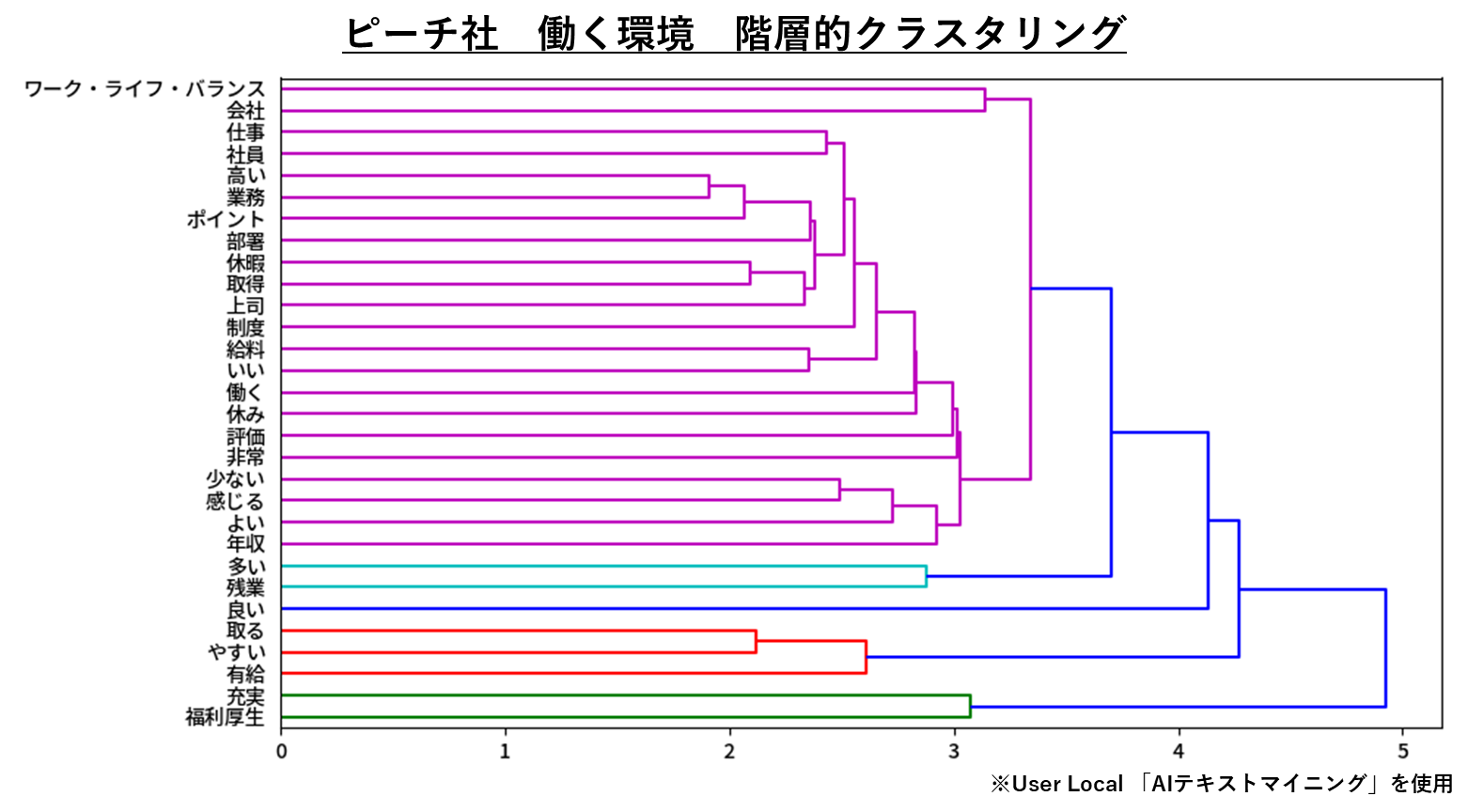
5-2 番外編②:(ID-)POSデータの分析
最近は小売店が保有するID-POSデータの整備が進み、その活用法に関する議論が盛んにされています。ここではID-POSデータの分析に関して代表的なものをご紹介いたします。
ABC分析
ABC分析は、売上を分析する初歩的な手法で、「重点分析」とも呼ばれます。ABC分析を行うことで、どの商品が売れ筋で、どの商品が死に筋かを判断することができるようになります。
ABC分析は以下の手順で行われます。

このランク付けから、商品の在庫管理に役立てたりします。例えばAランクの商品は売れ筋だと判断し、在庫に余裕を持たせるようにします。その一方でCランクは機会損失が小さいので必要最低限の在庫しか用意しません。
ABC分析は、「少数の商品が売上の大部分を占めている」というパレートの法則の考え方がもとになっています。そのため、何が売れ筋で何が死に筋なのかをしっかりと見極めることは在庫管理をする上で非常に重要になります。
デシル分析
購入金額に基づいて顧客を大きさの等しい10段階にランク付けする手法をデシル分析といいます。上位の顧客を高額購買客とみなし、プロモーションの対象にする活用がなされます。デシルのデシは「10分の1」を意味しています。
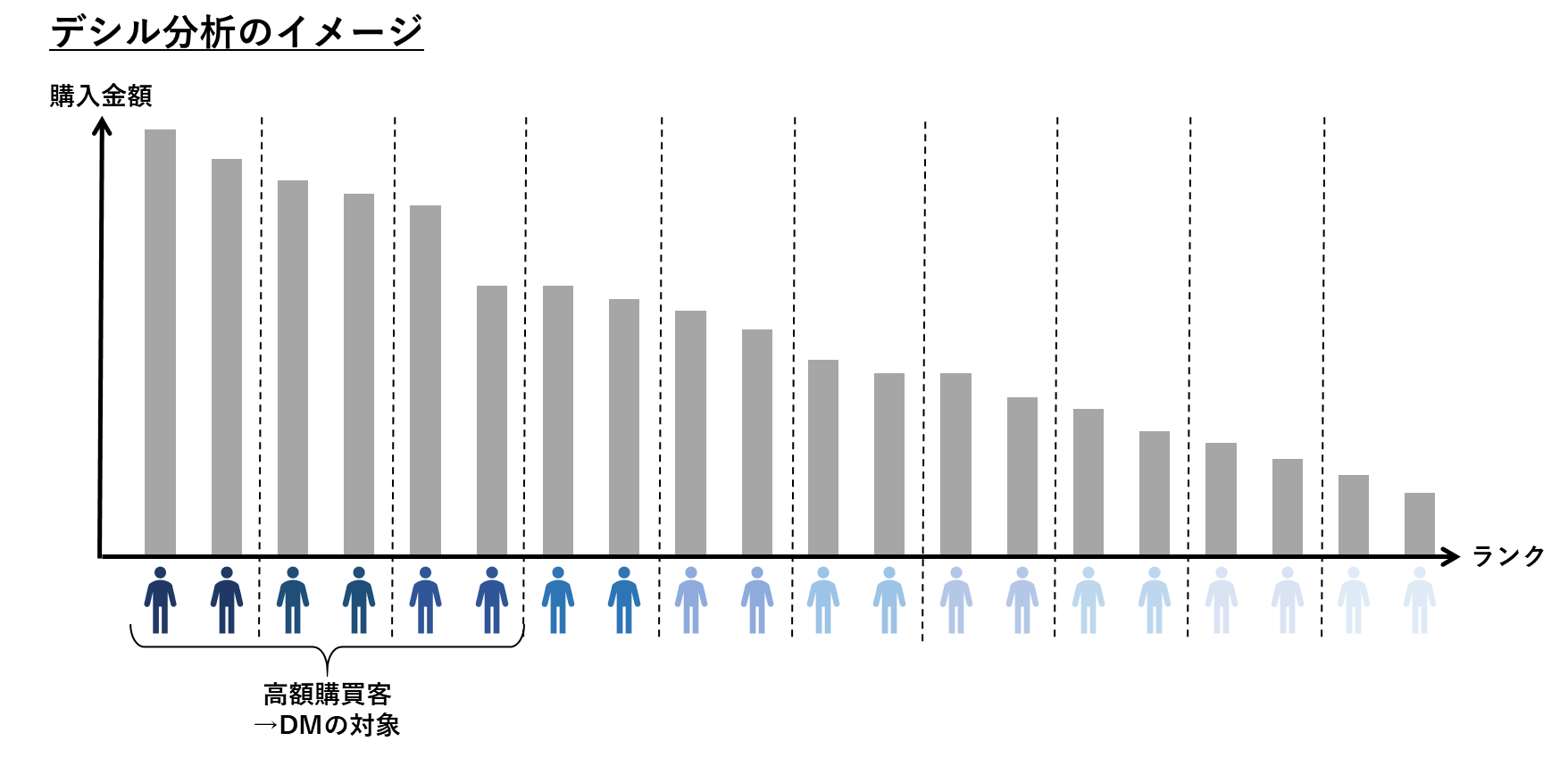
デシル分析は非常にシンプルで、マーケティングやデータ分析に詳しくない人でも扱いやすいです。しかしその一方で金額しか見ないシンプルさのため、深い分析には至りません。デシル分析をさらに細かい粒度で分析する手法の一つがRFM分析と呼ばれるものになります。
RFM分析
RFM分析は、Recency(最新購入日)、Frequency(購入頻度)、Monetary(購入金額)の3つの指標で顧客を分類する手法です。この手法は、企業にとっての顧客の優良度を測るのに用いられます。このRFM分析のうちMを詳細に見ていくのがデシル分析だといえます。

この3指標を使用して、顧客をランク付けしていきます。そして高ランクの基準に当てはまる顧客に対して、DMなどのCRM施策を積極的に行うことが多いです。

このランク付けに決まったルールはありません。企業ごとの戦略に従ってその基準を設定する必要があります。
アソシエーション分析(バスケット分析)
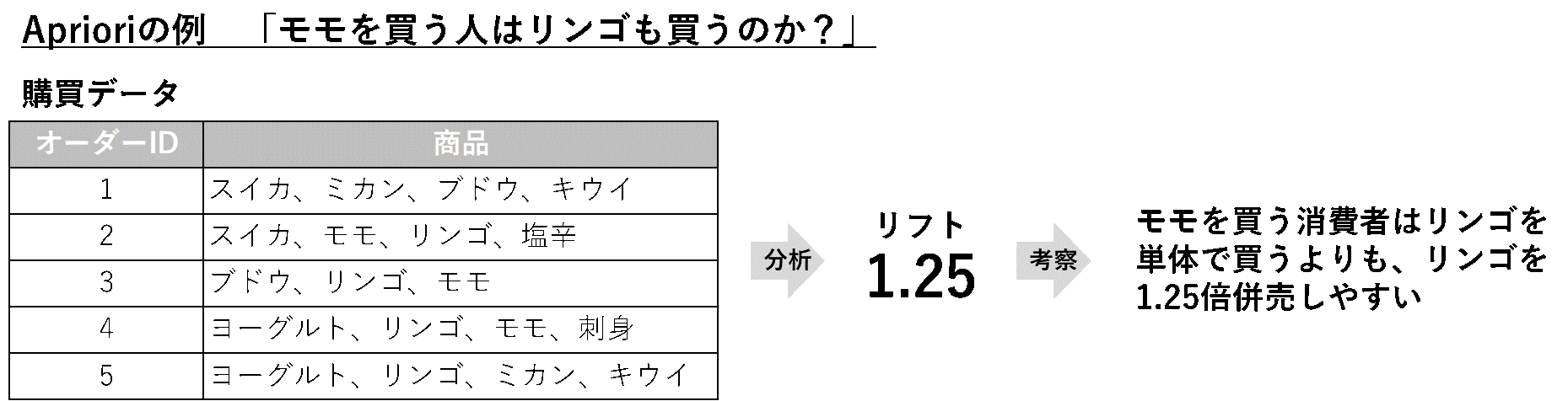
アソシエーション分析は、「何と何が同時に発生しやすいか」を分析するのに用いられる手法です。そしてアソシエーション分析のうち併売分析、すなわち「何と何が同時に購買されやすいか」を中心に分析を行うことをバスケット分析と呼びます。
有名な「ビールを買う人はオムツも一緒に買う」というのはアソシエーション分析を行うことで検証されています。
アソシエーション分析では、一般的には、支持度、確信度、リフトという3つの指標を用いたAprioriというアルゴリズムを用いて組み合わせを発見します。このうちリフトの高いルールを見つけ出す方法がよく用いられます。
少しややこしいので3指標の説明は割愛しますが、「単純に集計してるだけではないんだな」と覚えていただければ充分です。
まとめ
ここで紹介している分析手法は代表的であるものの、氷山の一角にすぎません。世の中にはまだまだ多くの分析手法が存在しています。
ただ肝要なのは、多くの分析手法を知ったうえで、目的に合わせた手法を適切に選択することだと思います。この適切に選択する作業は、まず手法を知らないことにはなし得ません。
この記事をきっかけに、データ分析の手法に関する理解の幅を広げていただければ幸いです。
データのことなら、高い技術力とビジネス理解を融合させる私たちにご相談ください。
当社では、データ分析/視覚化/データ基盤コンサルティング・PoC支援に加え、ビジュアルアナリティクス、ダッシュボードレビュー研修、役員・管理職向け研修などのトレーニングを提供しています。組織に根付くデータ活用戦略立案の伴走をしています。






コメント