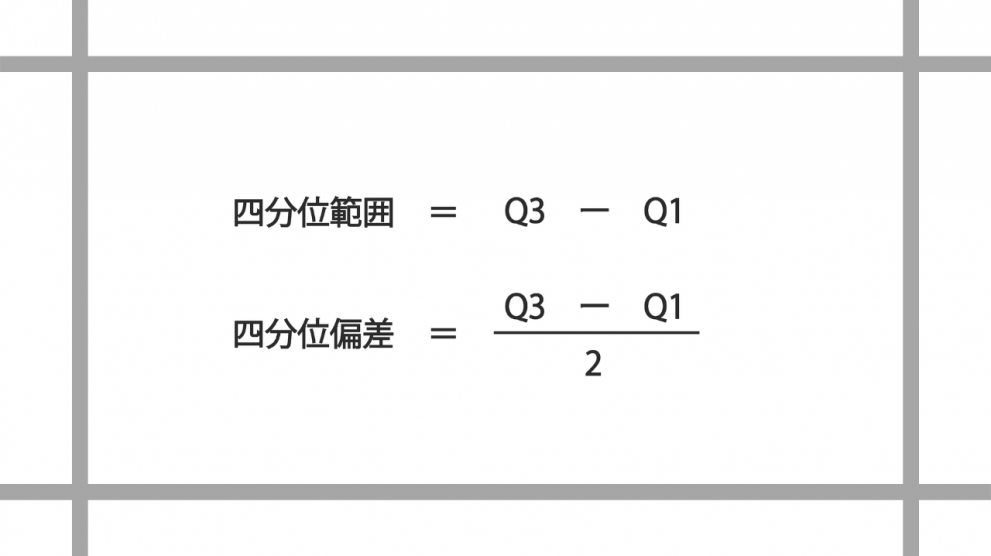
四分位範囲とは、データのちらばり具合を求めるもので、第1四分位数から第3四分位数までの範囲(データの中央50%部分の範囲)のことを指します。
一方で四分位偏差とは、この四分位範囲を二等分した値のことを指します。
統計検定の問題にも度々出題される四分位範囲・四分位偏差について、本記事では図解を用いて分かりやすく解説いたします。
1.四分位範囲は第1四分位数と第3四分位数の差分である
四分位範囲のイメージは以下です。
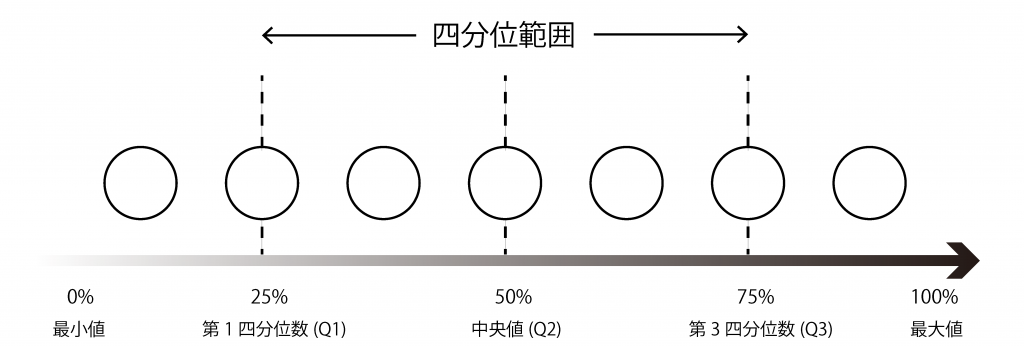
四分位範囲を理解するために、まずは「四分位数」を理解する必要があります。
四分位数とは、データを小さい順に並べたときに、そのデータの数で4等分した区切り値(25%、50%、75%)を指します。それぞれ小さい方から第1四分位数(Q1)、中央値(Q2)、第3四分位数(Q3)と呼びます。
そしてこの四分位数を使って四分位範囲の求め方を式に表すと下記の通りになります。
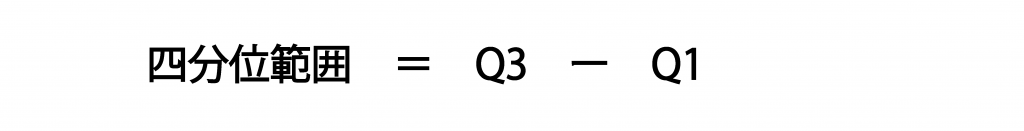
四分位範囲が大きければ大きいほど、データの散らばり具合は大きく、四分位範囲が小さければ小さいほどデータが密集しているといえます。
四分位範囲はデータのばらつきを比較したいときに活用する
四分位範囲はデータのばらつきを比較したいときに活用されます。
例えば、下図はある高校のクラスA、クラスBにおける生徒11人の数学におけるテストの点数を低い順に並べたものになります。
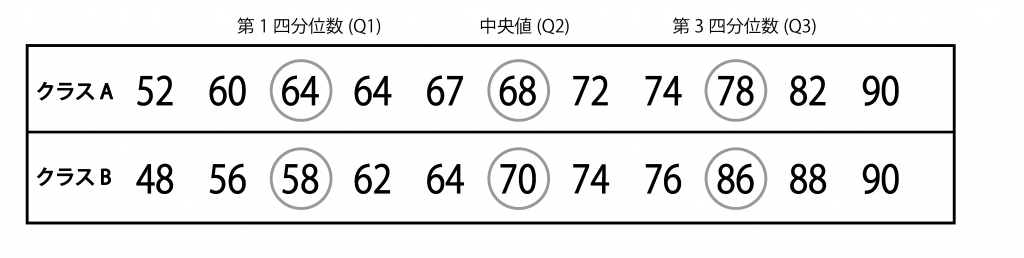
表をもとにそれぞれの四分位範囲を求めると、下記の通りになります。
クラスA:78(Q3)-64(Q1)=14
クラスB:86(Q3)-58(Q1)=28
上記では、クラスBの四分位範囲の方が大きいので、クラスAの数学におけるテストの点数より、クラスBの数学におけるテストの点数のばらつきが大きいとわかります。
2.四分位偏差とは四分位範囲を二等分した値
四分位範囲と類似した概念で、四分位偏差があります。四分位偏差とは四分位範囲を二等分した値です。式に表すと、下記の通りになります。
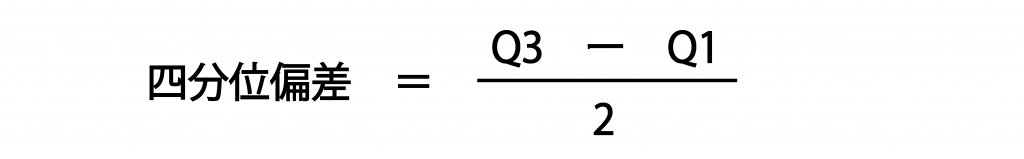
四分位範囲と同じくデータの散らばり具合を表す指標となっておりますが、わざわざ二等分する理由としては、四分位範囲では中央値からQ1、Q3がどのくらい離れているか掴めないためです。
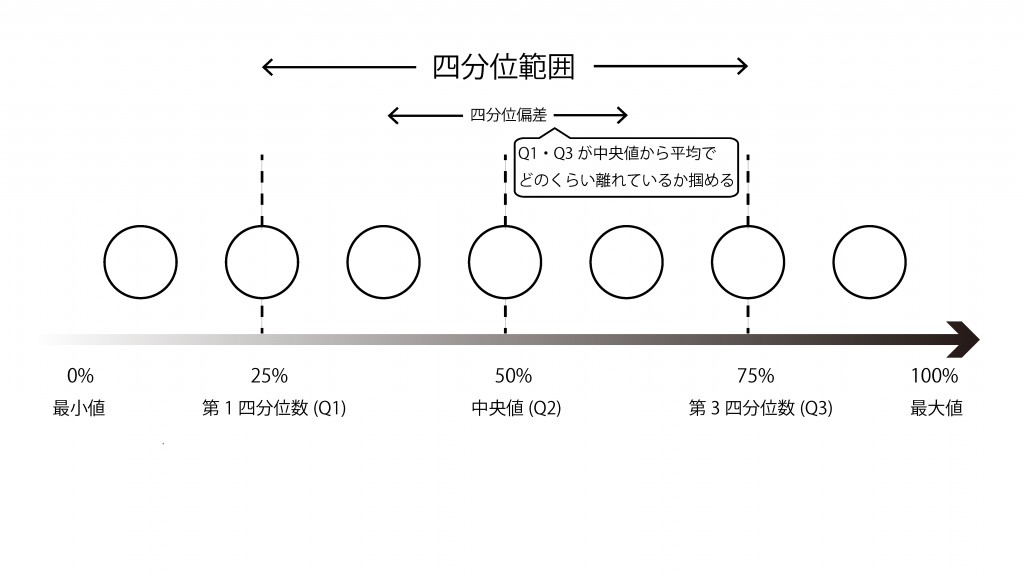
四分位偏差のメリットとして、四分位範囲の値を二等分することにより、Q1、Q3が中央値から平均でどの程度離れているかを掴むことができることが挙げられます。
そのため、四分位偏差を使えば四分位範囲よりも更に中央に密集したデータを把握できます。
まとめ
今回は、統計検定でもよく出題される四分位範囲について、その定義や特徴、四分位偏差との違いまで簡単に解説いたしました。
データのばらつきを掴むための指標は四分位範囲や四分位偏差の他にもいくつか存在します。標準偏差はその代表であり、平均値では表すことのできないデータのばらつきを掴むために使われます。興味のある方はこちらの記事も併せてご一読下さい。
『標準偏差とは?意味から求め方、分散との違いまでわかりやすく解説』
なお、統計検定の受験を控えている方に向けて、統計検定3級の効果的な対策をまとめた以下の記事をおすすめします。ぜひご活用下さい。





コメント