
データ分析や統計学の本を読んだら、必ずと言っていいほど目にする「標準偏差」というキーワード。
この標準偏差について下記のような疑問をお持ちの方は多いと思います。
- 「標準偏差とはどういう意味なんだろう?」
- 「標準偏差はどうやって見ればいいの?」
- 「標準偏差は実際に仕事で何の役に立つの?」
標準偏差は統計学を勉強していく中で出てくる正規分布やカイ二乗分布、t分布などのベースとなっているので、標準偏差をしっかりと理解することは統計学を学ぶ上で最も重要であるといっても過言ではありません。標準偏差をあまり理解せずに統計学の勉強を進めてしまったせいで、
「難しい。理解できない、、、」
と統計学に挫折する方は非常に多いです。
そこで、この記事では標準偏差の意味や具体的な求め方、実際のビジネスでの活用事例についてわかりやすく解説します。標準偏差を理解すると日常生活や仕事の見え方が変わってくるはずです!
目次
1.標準偏差は平均値では表せない”データのばらつき”を知るための便利なツール
標準偏差とはデータの特徴を要約する基本統計量の一つで、「データが平均値の周辺でどれくらいばらついているか」を表します。
ヒストグラムで表すと、以下の通りです。
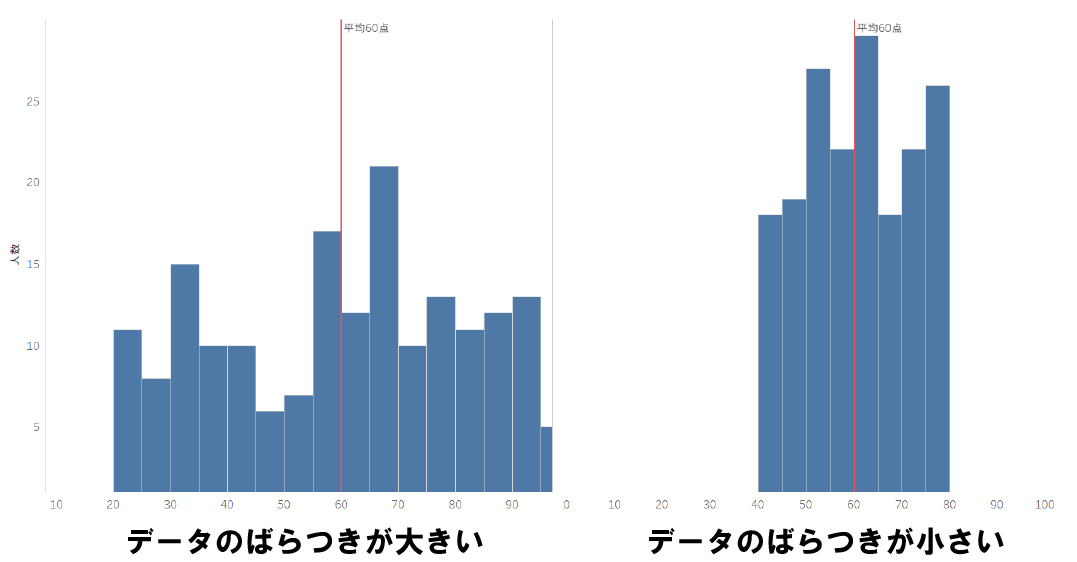
上図のように平均値が同じデータであっても、平均値からのデータのばらつき具合が全く異なるデータというものはよくあります。標準偏差はこのように平均値だけではわからないデータのばらつきを知るために有効なツールです。
標準偏差を理解するにはまず平均値の差である「偏差」を理解することが重要です。
1-1.偏差は平均値からの差である
偏差とは平均値からの差です。これは各データがそれぞれ「平均値からどれくらい大きい(小さい)のか?」を表しています。
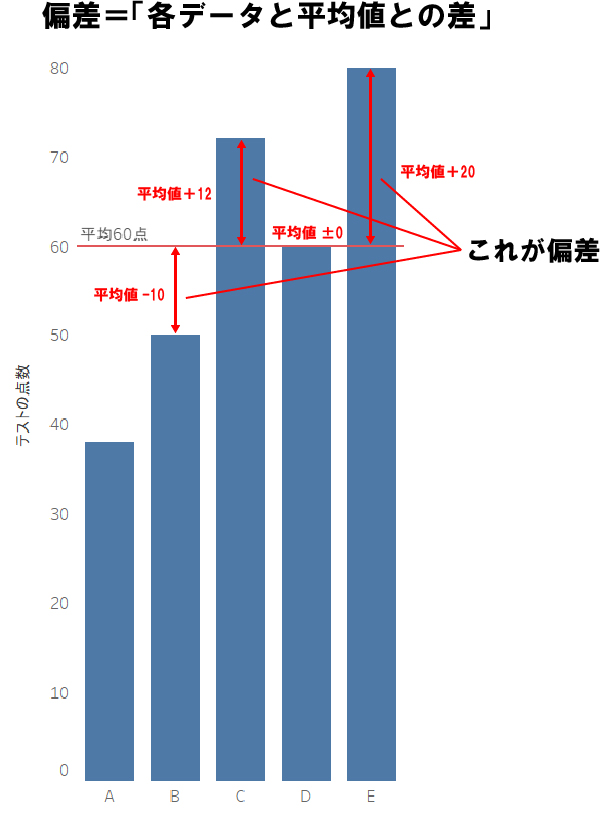
例えば、上記図の平均点が60点のテストで、Bさんは50点、Eさんは80点だったとします。その場合の各データの偏差は下記のとおりです。
- Bさん:50点ー60点=-10点(平均点より10点小さい)
- Eさん:80点ー60点=+20点(平均点より20点大きい)
偏差が理解できてしまえば、標準偏差の意味を理解するのは簡単です。標準偏差は「標準的な偏差」=「標準的な平均値との差」と訳せます。つまり、「このデータの偏差(平均値からの差)が標準的にこれぐらいですよ。」ということを表しているものです。
1-2.標準偏差でデータ全体の中での位置を把握できる
標準偏差を知れば、「各データがデータ全体の中でどの位置にいるか?」ということを理解できます。
つまり、標準偏差を知ることで下記のことがわかります。
- 標準偏差が大きい=平均値から離れているデータが多い=データのばらつき具合が大きい
- 標準偏差が小さい=平均値から近いデータが多い=データのばらつき具合が小さい
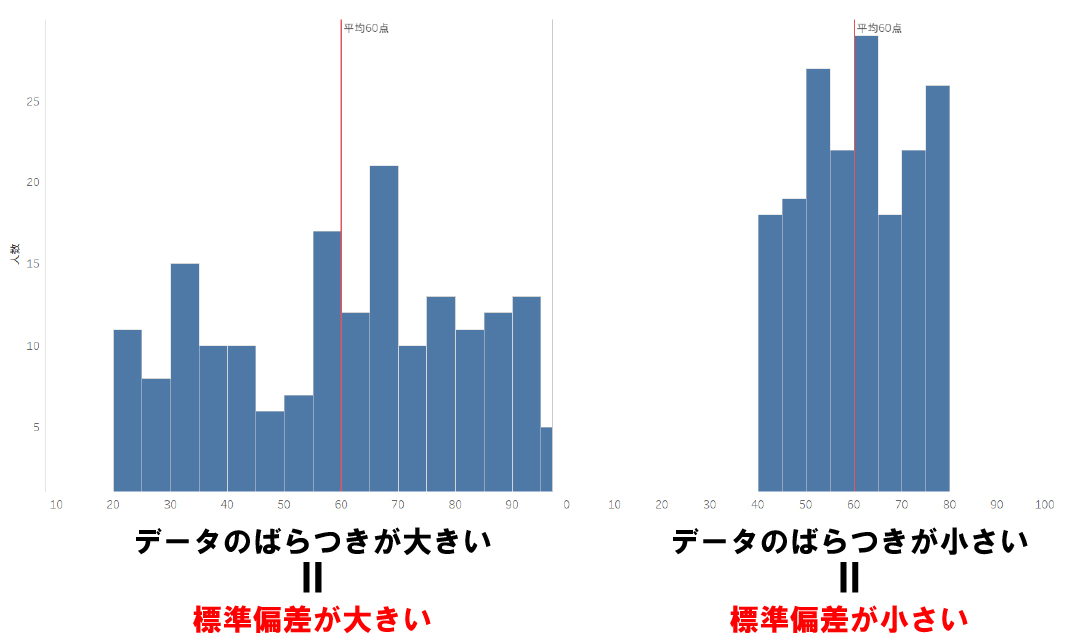
標準偏差によってデータの捉え方が変わる
標準偏差を知ることにより、データの捉え方が変わります。
例えば、あなたが数学のテストで全体の平均点が60点の中で50点を取ったとします。その時に平均点と自分の得点だけしか情報がないと、「平均点より少し低かったけど頑張った方だな。」と思うかもしれません。
しかし、このテストの標準偏差が5点だったら、自分の点数に対する捉え方がガラッと変わります。この場合、多くの人が平均点に対して60点±5点=55点~65点の範囲内にいることになるので、50点を取ったことに対して「まずい点数を取ってしまったな、、、」と凹むことになります。
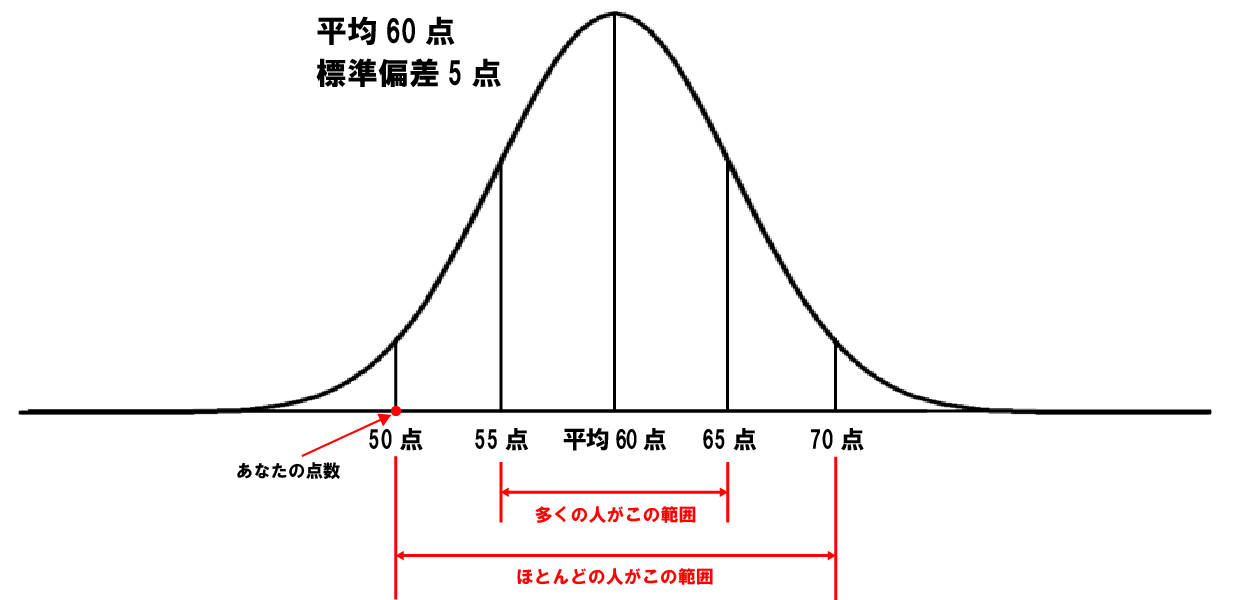
このように平均値だけでなく、標準偏差を知ることで、各データが全体のデータの中で下記のどちらなのかを理解できるようになります。
- 珍しいデータなのか?
- よくあるデータなのか?
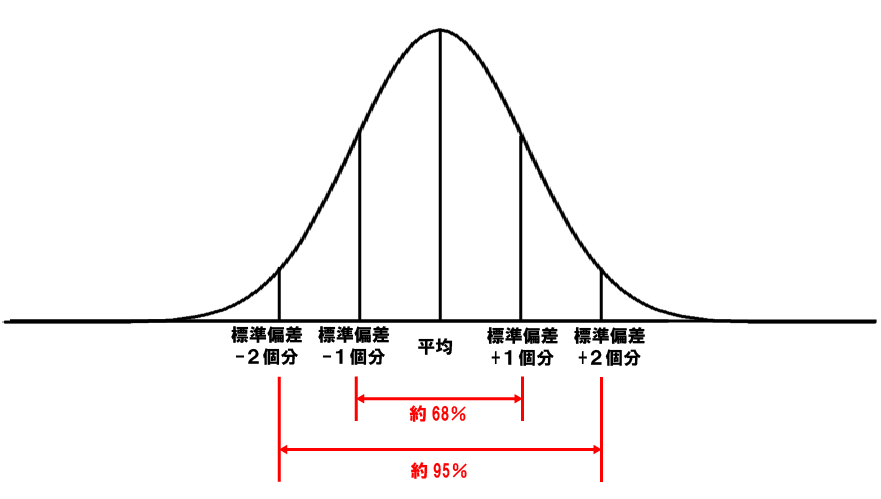
上記を知るために便利なのが標準偏差の68%ルールと95%ルールです。
1-3.標準偏差の68%ルールと95%ルール
標準偏差には下記のようなルールがあります。
- 平均値から±標準偏差1個分に含まれるデータは全体の約68%を占める
- 平均値から±標準偏差2個分に含まれるデータは全体の約95%を占める
※どちらのルールもデータの分布が下記のような正規分布に従う前提
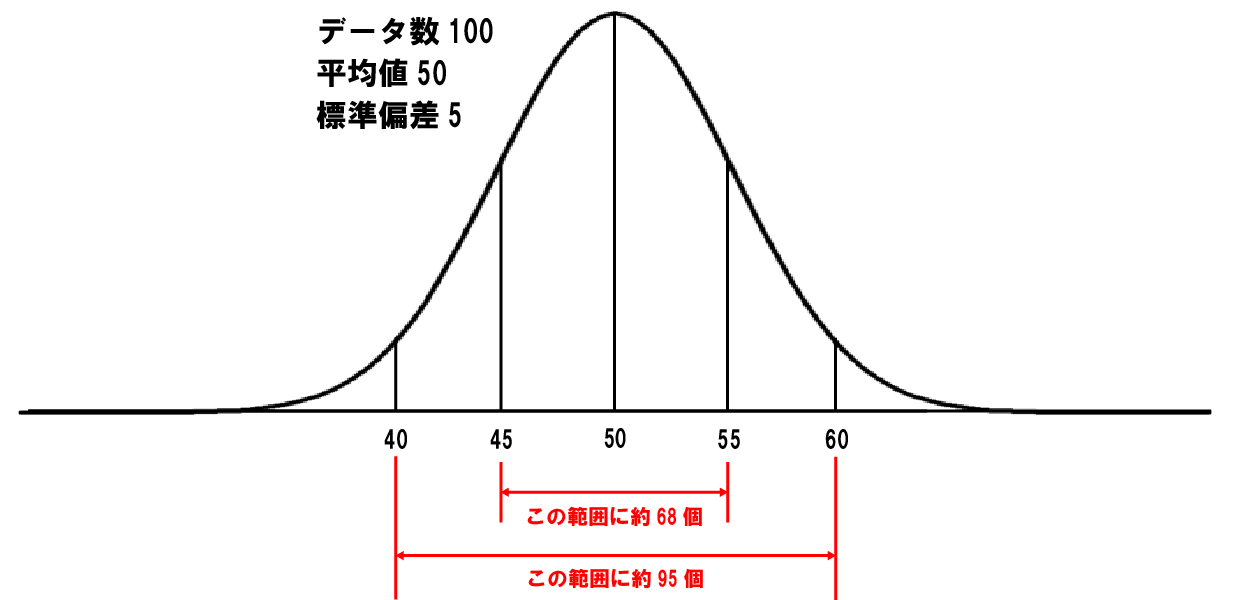
例えば、データの数が100個あり、その平均値が50、標準偏差が5である場合、平均値±標準偏差1個分離れているというのは50±5という意味です。つまり、45~55の範囲内に68%のデータ、つまり100×68%=約68個のデータが含まれるということを意味しています。
この68%ルールと95%ルールを知っているとものすごく便利です。なぜなら、あるデータが平均値+標準偏差1個分以上の場合、全体の上位16%(平均値-標準偏差1個分の場合も同じく16%)ということがわかりますし、平均値+標準偏差2個分以上だった場合は上位2.5%以内に入るということがわかるからです。
このように、あるデータのデータ全体における位置を知るには、平均値だけでなく、「そのデータが平均値から標準偏差何個分離れているか?」を基準に捉える、これがすごく有効です。
各データが標準偏差何個分であるかを知るには
(データー平均値)÷標準偏差
の式で計算することができます。例えば、平均値50点、標準偏差5点の場合にあなたが65点を取ったとします。
この場合、この65点が標準偏差何個分かというと
(65点ー50点)÷5点=15点÷5点=3
となり、標準偏差3個分となります。
統計データ可視化を成功させる95のチェックリストをダウンロードする
2.初心者が混乱しがちな3つのポイント
標準偏差についてよく混乱しがちなポイントを3つご紹介します。
2-1.標準偏差 Xとは「各データが平均値から標準的にX離れている」という意味
標準偏差 Xの意味は「各データが平均値から標準的に X 離れている」ということです。
例えば、平均値50、標準偏差10の場合は「平均値50に対して、各データが標準的に10離れている」という意味になります。つまり、平均値50±10=40~60の範囲に全データの約68%が含まれているということがわかります。
2-2.分散は標準偏差を二乗した値
分散は標準偏差を二乗した値です。標準偏差との関係性は下記のとおりです。

例えば、下記のようになります。
- 標準偏差10の時、分散=標準偏差²=10²=100
- 標準偏差5の時、分散=25
分散と標準偏差はよく似ている
分散は標準偏差と特徴がよく似ており、分散を知ることで下記のことがわかります。
- 分散が大きい=平均値から離れているデータが多い=データのばらつき具合が大きい
- 分散が小さい=平均値から近いデータが多い=データのばらつき具合が小さい
分散の難点
分散は数学的にものすごく便利なのですが、標準偏差を2乗しているので、単位が変わってしまうのが難点です。例えば、標準偏差5分の場合、分散25分² となるので、分散を見るだけでは実際に平均値からどれくらいばらつきがあるかが直感的にわかりにくいのです。そのため、実際に平均値からどれくらいばらつきがあるのかを把握するためには標準偏差が使われます。
2-3.偏差値は標準偏差がベース
偏差値は平均が異なるテストの点数を同じ物差しで比較するために生み出されたものです。受験において非常に認知度の高い偏差値ですが、実は標準偏差がベースとなっています。
偏差値は平均値を50、標準偏差1個分のずれに対して10の値を与えるという形を取りますが、具体的な計算方法や詳細な違いは標準偏差の計算方法の理解が必要なので、後ほど詳しく解説していきます。
3.身近な例を「標準偏差」を使って考える
標準偏差をより身近に感じてもらうために2つ例を挙げます。
3-1.1年間の体重変動
1年間の体重変動について標準偏差を基準に見てみます。1年間毎月体重を記録したAさんとBさんがいます。二人とも平均体重は65kgでした。ただ、それぞれの1年間の体重に関する標準偏差は下記のようになりました。
- Aさん:10kg
- Bさん:1kg
Aさんの場合、標準偏差が10kgなので、平均体重65kgに対して±10kg(55kg~75kg)の変動が標準的にあったことを意味しています。これはなかなかの変動幅ですよね!?恐らくAさんは食生活が安定せず、ダイエットとリバウンドを繰り返しているかもしれません。
一方、Bさんの標準偏差は1年間で1kgなので、平均値65kgに対して、±1kgの変動が標準的にあったということです。つまり、1年間で体重が64kg~66kgに収まる時が多かったようです。このように標準偏差を見れば、Bさんは食生活が安定していそうだということがわかります。
このように、平均値だけではわからなかったことが、標準偏差を見ることでわかるようになります。
3-2.電車とタクシーの到着時刻
もう1つ例を挙げます。「電車の到着時刻とタクシーの到着時刻」についてです。出張の交通手段で電車かタクシーを選ぶ必要があるという場面を想像してください。
それぞれの到着時刻の遅れの平均は
- 電車:平均3分
- タクシー:平均5分
この場合、タクシーの方が乗り換えもなく楽なので、この程度の到着時刻の違いならタクシーを選ぶかもしれません(費用は考慮から外しています)。しかし、標準偏差を見てみると下記の通りでした。
- 電車:標準偏差2分
- タクシー:標準偏差20分
この場合、電車だと標準的に平均3分±2分、つまり1分~5分の遅れになる可能性があります。一方、タクシーの場合は平均5分±20分、つまり予定時刻よりも15分早く到着する場合もあれば、25分遅れる場合もあるということです。
これがわかれば、約25分も遅刻する可能性のあるタクシーは選ばないことが多くなるでしょう。このように標準偏差は平均値だけでは判断できないことを教えてくれるので大変便利です。
4.標準偏差を求める4つのステップ
次に標準偏差の求め方についてお話ししていきます。標準偏差は下記4ステップで求めることができます。
- step1:平均値を求める
- step2:偏差を求める
- step3:分散を求める
- step4:平方根を求める
では、1つずつのステップを具体例を交えながら詳しく確認してみましょう。
4-1.step1:平均値を求める
1章でお話しした通り、標準偏差は平均値をベースとしています。そのため、まず平均値を求める必要があります。
例えば、下記のようなテスト結果データがあるとします。

この場合、平均点=(60+83+72+68+93+45+78+65+54+42)÷10=66点 と求められました。
4-2.step2:偏差を求める
次に偏差を求めていきます。偏差とは「各データにおける平均値の差」でしたね?そのため、平均値がわかっていれば、偏差を求めるのはものすごく簡単です。

なので、この例でいうと

という式で計算することができます。
実際に偏差を求めてみると下記のようになります。
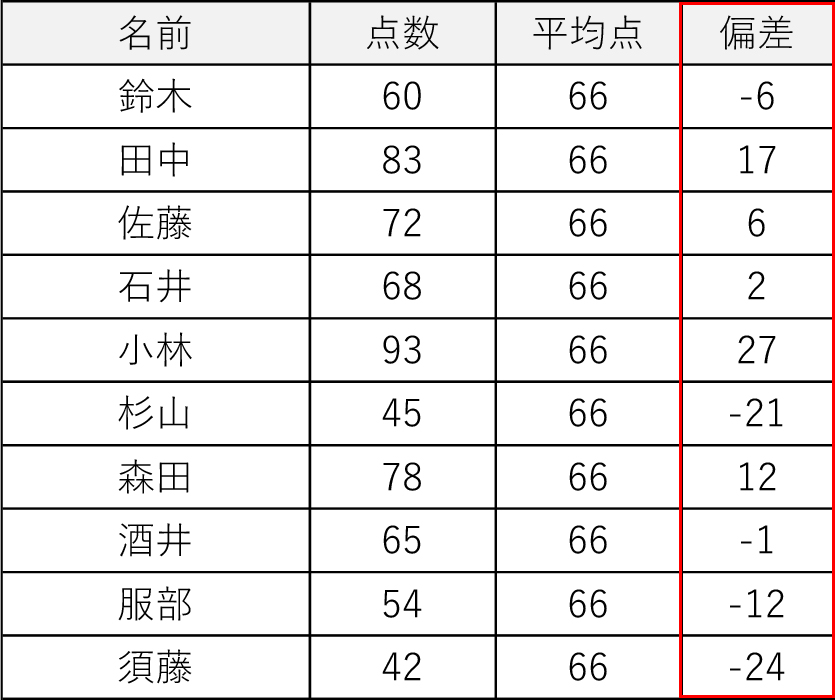
これで偏差(平均値との差)を求めることができました。
4-3.step3:分散を求める
偏差がわかったので、次に分散を求めます。
分散は下記の式のように、各データの偏差を二乗し、それを全て合計した後にデータの個数で割ることで求めることができます。

では、実際に分散を計算していきましょう。
分散はまず偏差を二乗し、それを全て足し合わせていきます。偏差の二乗が出せたら、それを合計し、データの数で割ることで分散を求めることができます。
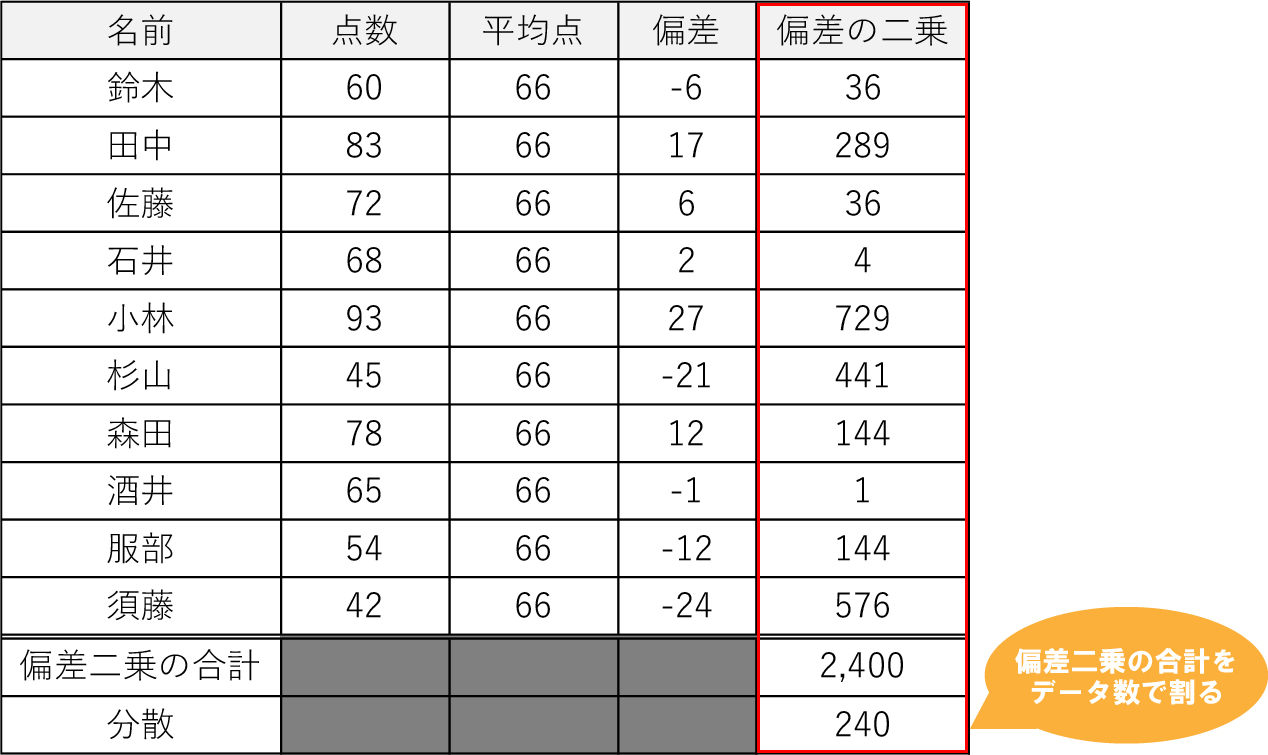
今回の例だと
分散=(36+289+36+4+729+441+144+1+144+576)÷10=2,400÷10=240
ということで分散=240ということがわかりました。
偏差の平均を取らない理由
私が統計学を学び始めた時は、このステップで「なぜ急に分散が出てきたの?偏差を平均すればいいんじゃないの?」と頭が混乱しましたので(笑)、その疑問についても解消したいと思います。
なぜ偏差の平均ではなく、一度偏差を二乗して分散を求める必要があるのでしょうか?
それは偏差の平均をとると必ず0になってしまうからです。今回の例のようにそれぞれの偏差はプラスもあれば、マイナスもあります。そのため、全てのデータの偏差を足し合わせると、そのプラスマイナスで相殺され、合計すると必ず0になります。
今回の例で見てみましょう。
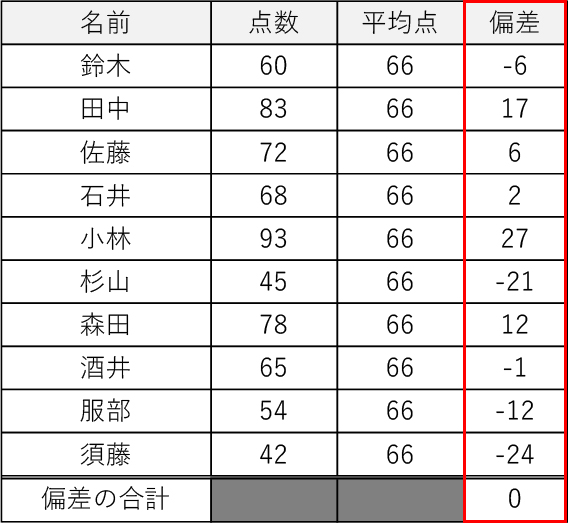
偏差の合計=(-6+17+6+2+27-21+12-1-12-24)=0
となることが実際に計算してみるとお分かりになると思います。この原因は偏差がプラスとマイナスどちらの値もあり、相殺し合ってしまうからです。そのため、標準偏差の計算では偏差を二乗し、その平均を取ることで、マイナスの符号を除去しているのです。
4-4.step4:平方根をとる
いよいよ最後のステップです。平方根をとります。
step3までで分散=240ということがわかりました。ただ、この分散はそのままでは使えません。なぜならこの分散は偏差を二乗しているので、「点²」という単位になっており、単位も二乗されてしまっているからです。
そのため、二乗されている単位を元に戻すために分散の平方根を取る必要があります。
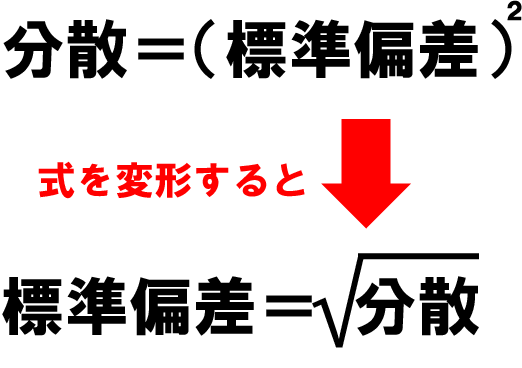
これが標準偏差です。
今回の例を当てはめてみると
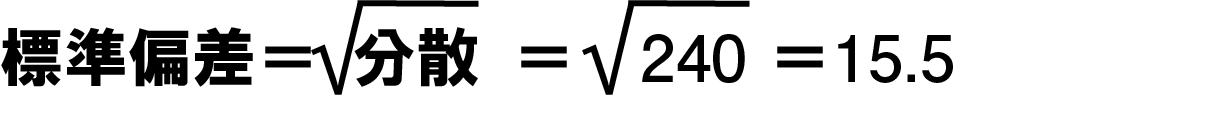
となり、標準偏差=15.5点ということがわかりました。この結果から、平均点66点±15.5点の範囲内に全データの内、約68%のデータが含まれる、ということがわかります。
※データの分布が正規分布になっていることを前提としています。
いかがでしたか?この流れを覚えてしまえば、標準偏差は簡単に出すことができます。
4-5.標準偏差の公式
実は標準偏差には公式があります。「最初から言ってよ。」と思われるかもしれませんが、数学が苦手な方はこれを見た瞬間に以前の私のようにアレルギー症状が出ますので、最後に持ってきました。
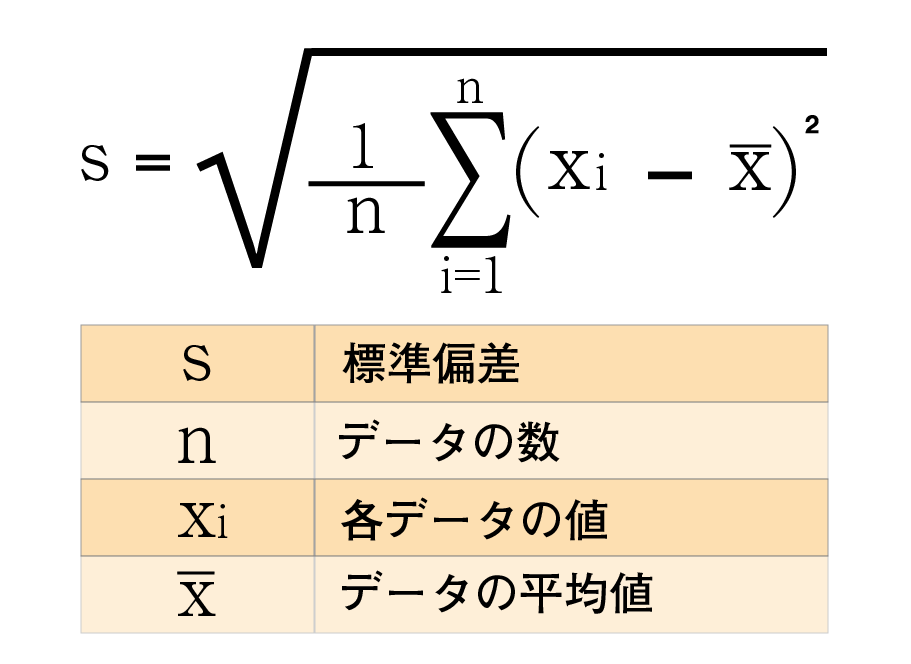
※標準偏差は母標準偏差だと「σ」、標本標準偏差だと「s」で表されますが、ここでは標本標準偏差を基準にお話をしています。
ただ、正直この公式を見ただけではよくわからないと思いますので、具体的な例に当てはめてみます。そもそも記号になった瞬間に「わかりにくい、、、」と感じる人も多いと思いますので、記号を置き換えてみましょう。

これで少しわかりやすくなりましたね。さらに、式のそれぞれの意味を確認してみます。
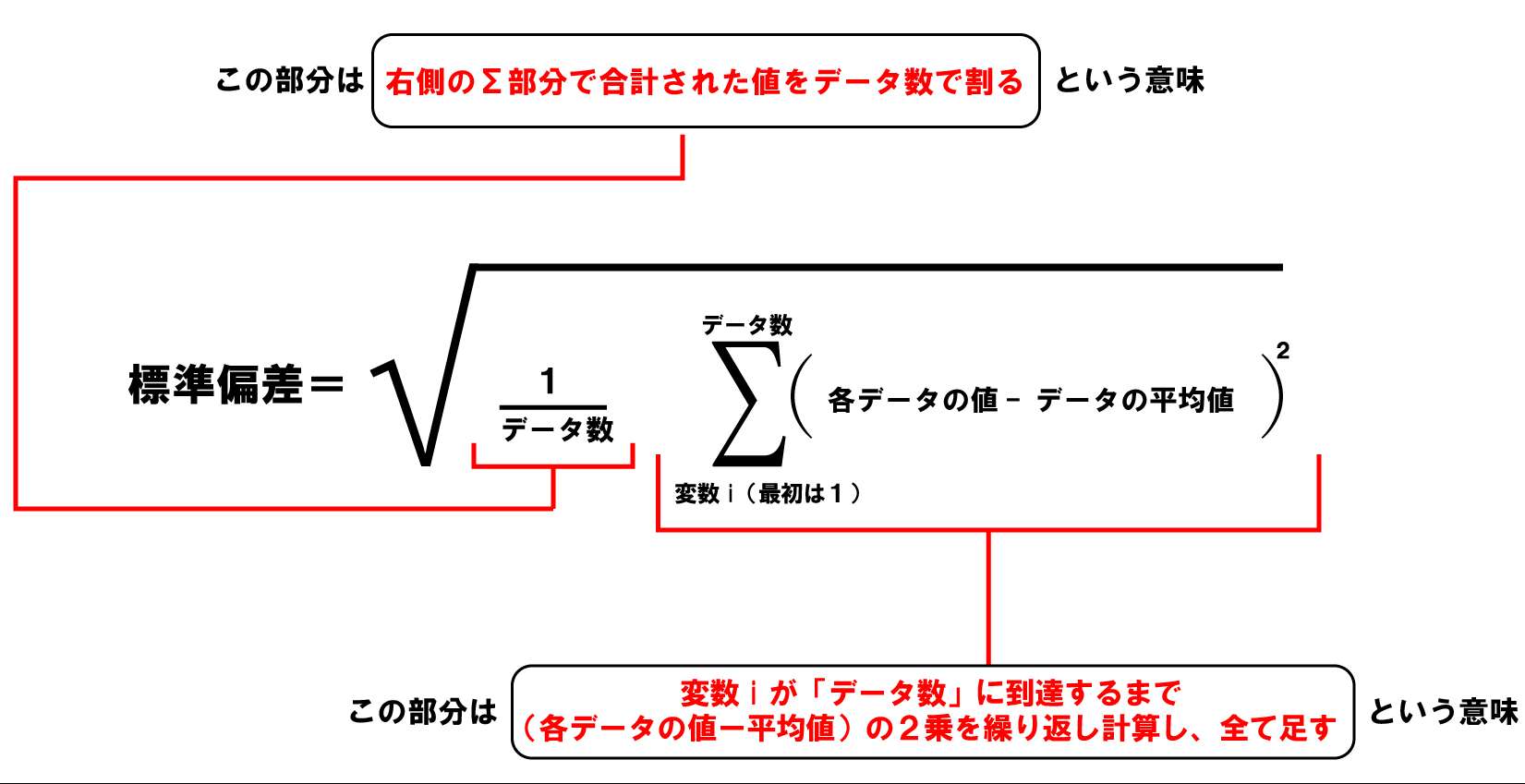
これで公式の式の意味がわかってきたと思いますので、先ほどの例に当てはめてみましょう。

このデータの平均点やデータ数は下記のとおりです。
- 平均点:66点
- データ数:10
これを公式に当てはめます。
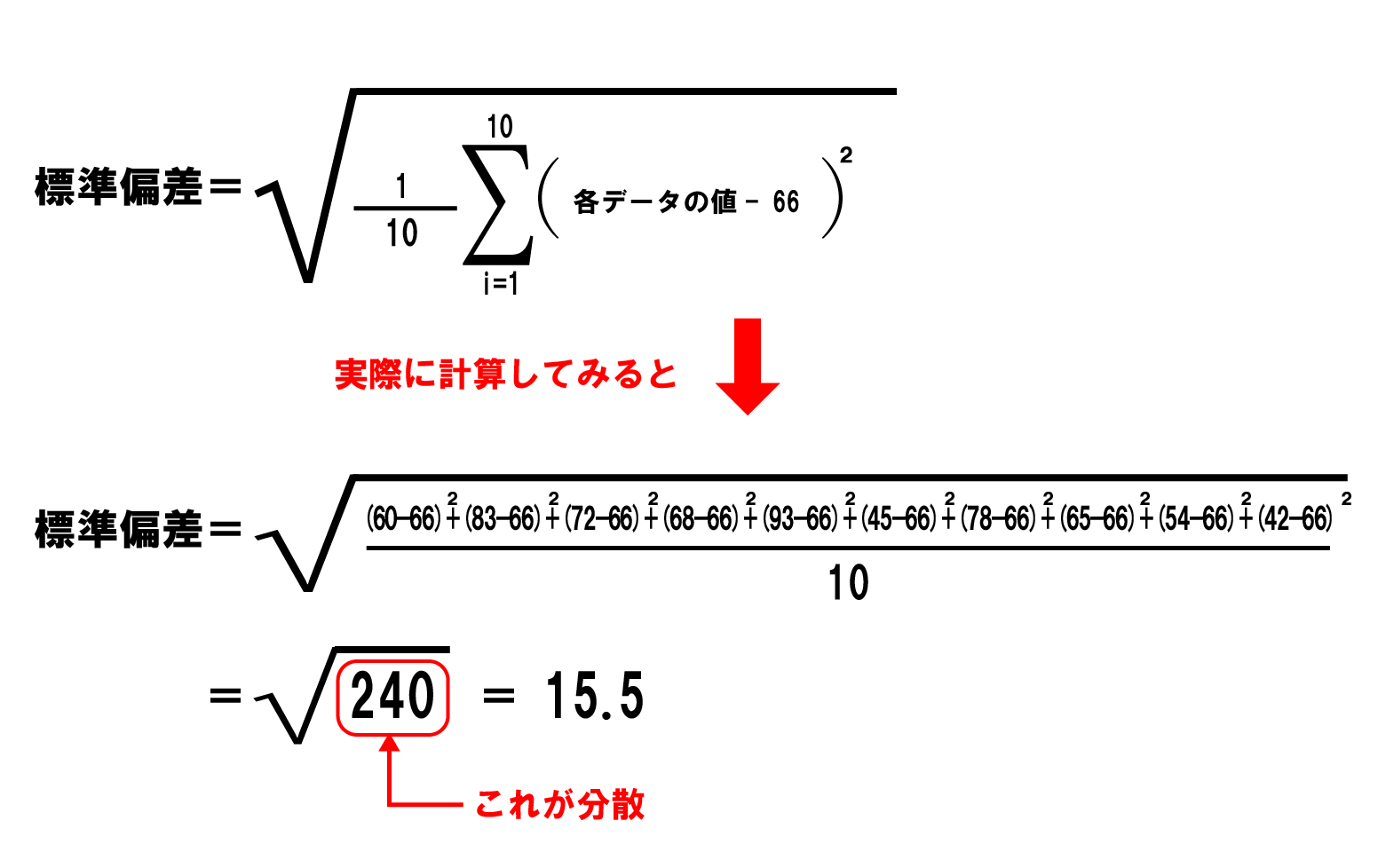
このように公式を使えば、上記のように簡単に標準偏差を出すことができます。ただ、公式を覚えて当てはめるよりも下記4つのステップで標準偏差を求められるようになった方が応用が利きます。
- step1:平均値を求める
- step2:偏差を求める
- step3:分散を求める
- step4:平方根を求める
5.仕事に活かせる標準偏差の利用シーン
ここまで標準偏差の概要から求め方までお話してきました。ただ、仕事をされている方にとって最も知りたいのは、「標準偏差が仕事にどのように利用されているのか?」ということだと思います。
そこで、この章では仕事に活かせる標準偏差の利用シーンをいくつかご紹介します。
5-1.1日の販売数を予測する
標準偏差は1日の来店客数を予測する時に利用することができます。
例えば、あるお店では1日に約200個程お弁当が売れていると考えて、仕入れをしていたとします。ただ過去1ヶ月分のお弁当の販売数を調べてみたところ、1日の平均販売数と標準偏差が下記の通りだとわかりました。
- 1日平均販売数:150個
- 標準偏差:20個
※お弁当の販売数のデータは正規分布に従うと仮定します。
これを前述の標準偏差の68%ルールと95%ルールに当てはめると、下記のことがわかります。
- 約68%の確率:1日の平均販売数=150個±20個=130個~170個の範囲に収まる。
- 95%の確率:1日の平均販売数=150個±(20個×2)=110個~190個の範囲に収まる。
このようにみれば、お弁当を1日200個仕入れているのは多すぎる、ということがわかります。このように標準偏差を知ることで売上予測や在庫量(仕入れ量)の最適化につなげることができます。
5-2.複数店舗の業績を比較する
複数店舗の業績を比較する際にも標準偏差が利用できます。A店舗とB店舗の1年間の月間平均売上高がともに500万円で、利益率もほとんど違いがなかったとします。これだけを見れば、A・Bどちらの店舗を優劣はつけにくいですが、月間売上高の標準偏差が下記の通りだった場合、話が全く変わってきます。
- A店:50万円
- B店:200万円
A店は約7割の確率で450万円~550万円の売上幅で安定的に売上を上げていて、今後も着実に売上を上げていけそうです。一方、B店は約7割の確率で300万円~700万円の売上高となり、かなり幅があります。平均月間売上高だけを見たら、「A店、B店ともに特に問題ない。」と判断していたかもしれませんが、標準偏差を把握することで「B店の標準偏差が大きい理由を分析しないといけない。」ということがわかり、次の行動につなげることができます。
5-3.株式投資のリスクの判定
コロナ禍で株式投資を始めた方も多いと思いますが、この株式投資でも標準偏差が利用されています。例えば、下記は東証一部のソフトバンク株式会社と東証マザーズの株式会社ZUUの日別の株価チャートです。左下部に標準偏差が載っています。
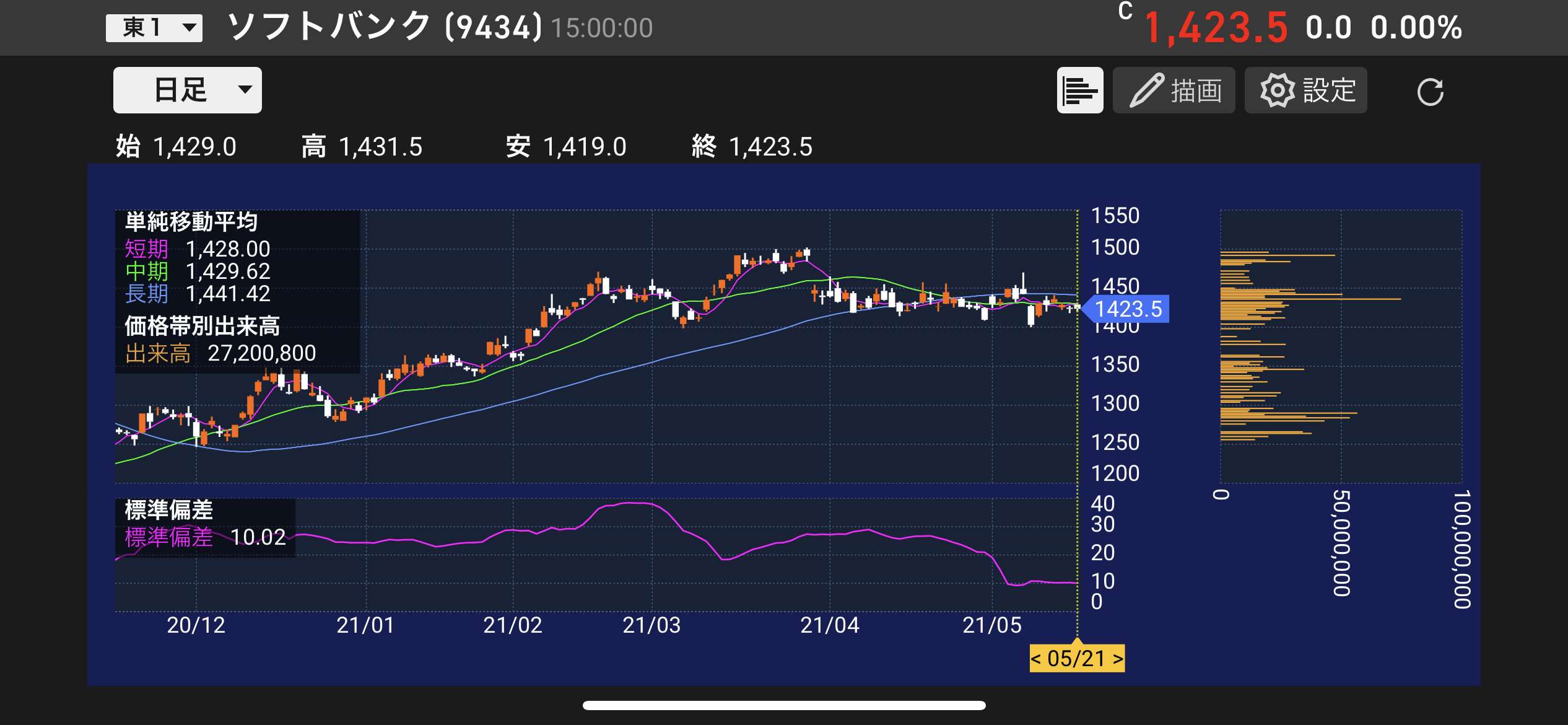
引用:楽天証券アプリより拝借
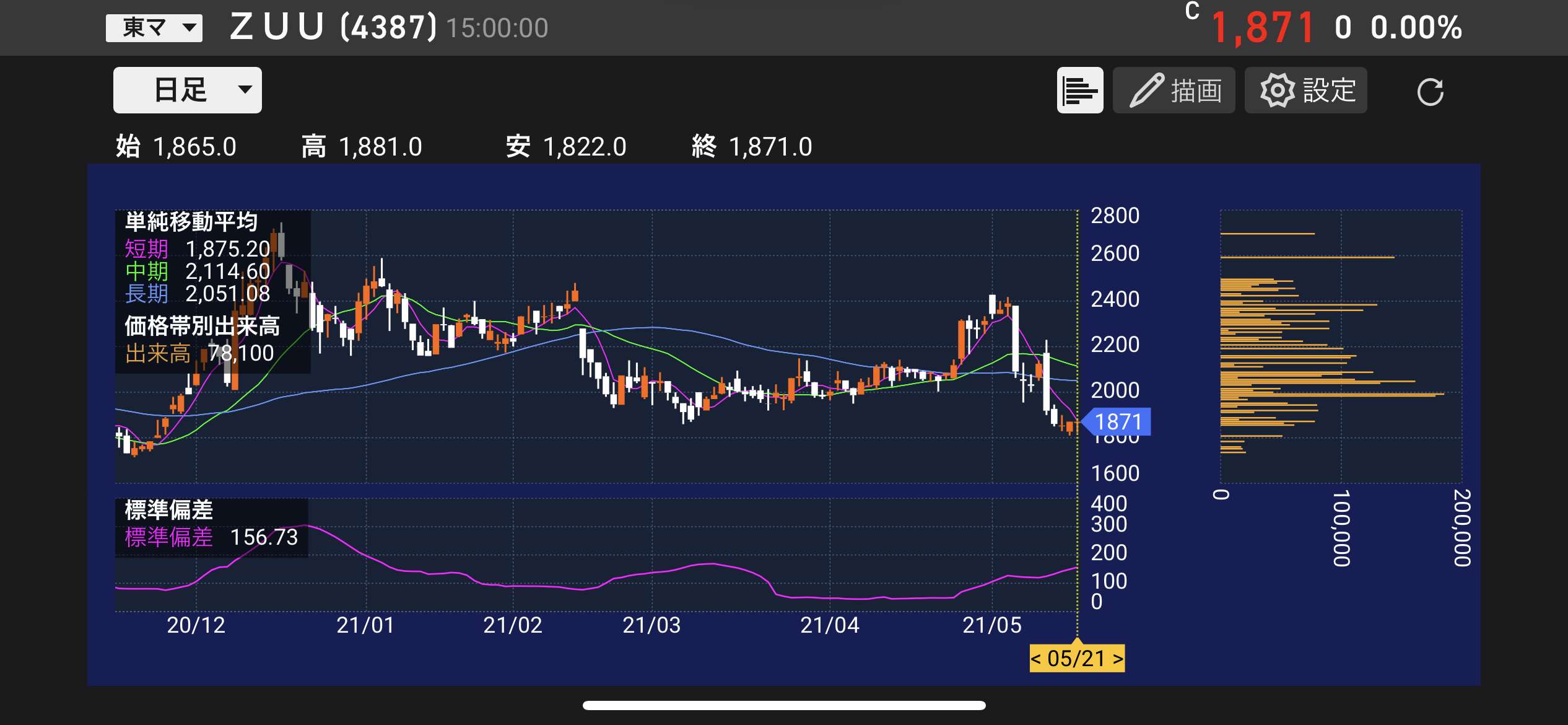
引用:楽天証券アプリより拝借
これを見ると、各企業の2021年5月21日時点の標準偏差は下記の通りです。
- ソフトバンク:10.02
- ZUU:156.73
この標準偏差の値を見れば、ソフトバンクは株価の変動が小さく、ZUUは非常に株価の変動が大きいということがわかります。
※2021年5月21日時点の話なので、あくまで参考程度に。
もしこの2択で株式を購入するかどうかを迷っている場合に、株式を買う目的が「株で大きく儲ける!」ということであれば、株価の標準偏差が大きいZUUの株を(もちろん、大損するリスクも覚悟したうえで)、「資産を分散してリスクに備えたい。」という方は標準偏差が小さいソフトバンクの株を買う、という選択になるでしょう。
このように標準偏差は実際に株式投資でも大いに利用されています。
5-4.品質管理における不良品判定の基準
製品の品質管理においても標準偏差が利用されています。
例えば、200gを1食パックとして各ラーメン店に納品している製麺所があるとします。機械の精度が低いため、1色パック198gや202gになる時もあり、そのまま出荷するとラーメン店からクレームを受けてしまいます。
こういう状況で「出荷前に一定の基準で不良品を取り除きたい。」という時に利用できるのが標準偏差です。標準偏差の特性を思い出してください。平均値±標準偏差2個分に全てのデータの中の約95%が入るんでしたよね!?
※データが正規分布に従うことを前提とします。
そのため、不良品の基準を「平均値±標準偏差2個分の範囲に入らないもの」という基準を決めれば、経験と感覚で基準を決めるよりも論理的で明確な基準にすることができます。
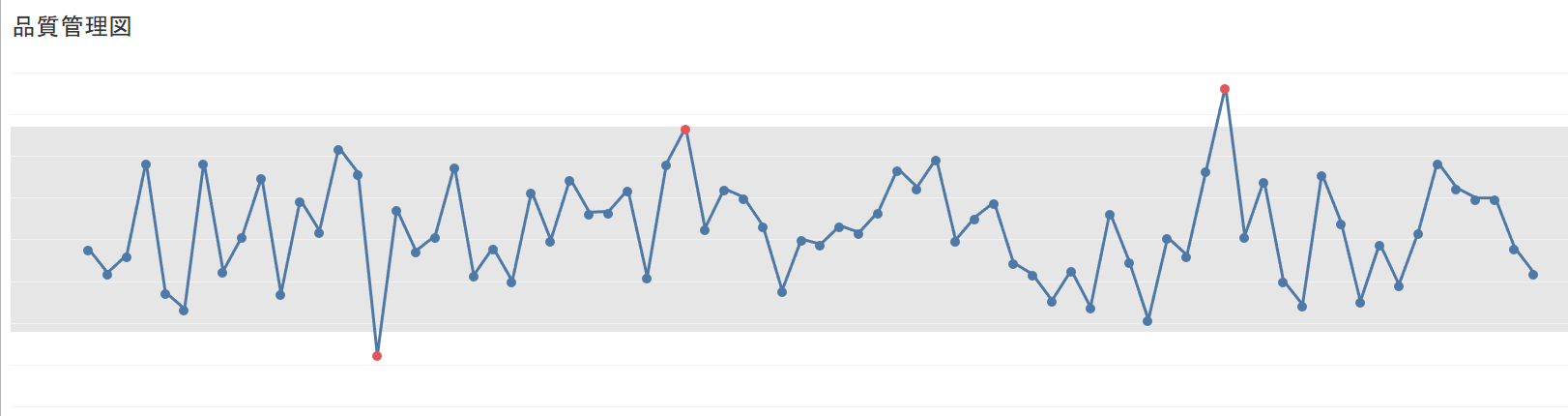
上記の図はTableauで作成した品質管理図ですが、1食200グラム(平均値)を基準として各製品の標準偏差2個分以内の範囲を灰色に塗りつぶして、各データを円で表して見える化しています。
基準をオーバーしたデータは赤色になっているのでパッと見で基準値外になっていることがわかります。この基準で管理すれば、全体の5%を占めるばらつきが特に大きいものは事前に除いて出荷できるので、ラーメン店からクレームが来る可能性を減らすことができます。もしこの基準でもクレームが来るなら、標準偏差1.5個分の範囲内にし、より基準を厳格にすれば対応が可能です。
この例はものすごく簡単な例ですが、標準偏差はこのような品質管理においてもよく利用されています。
6.偏差値は標準偏差の応用版
それでは最後に標準偏差の応用である「偏差値」についてご紹介したいと思います。
6-1.偏差値の計算方法
偏差値は平均点=偏差値50、標準偏差1個分のずれに偏差値10を与えています。具体的な計算式は下記のとおりです。

例えば、平均点が60点、標準偏差15点のテストがあるとします。このテストを上記の計算式に当てはめると下記の式になります。
偏差値=(テスト点数ー60点)÷ 15点×10+50
偏差値は平均点を偏差値50としますので、今回は平均60点=偏差値50。標準偏差1個分のずれに偏差値10を与えるので、標準偏差15点なので±15点ごとに偏差値±10が加えられます。そのため、もしテスト結果が75点だった場合は
偏差値=(75点ー60点)÷15点×10+50=60
となり、偏差値60になることがわかります。
6-2.偏差値の便利さ
偏差値のおかげで、各テストごとに違う平均点や標準偏差を同じ物差しで比べることができます。
前述のように偏差値は標準偏差1個分のずれに対して10の値を加えているので、標準偏差の68%・95%ルールに当てはめて考えると下記のことがわかります。
- 偏差値40~60(標準偏差1個分のずれ)に約68%のデータが含まれる
- 偏差値30~70の範囲内(標準偏差2個分のずれ)に約95%のデータが含まれる。
このように偏差値を知ることで自分が受験生の中で上位何%の位置にいるのか、ということをある程度把握出来ます。
まとめ
このように標準偏差とは平均値に対するデータのばらつき具合を表したもので、日常生活からビジネスまで幅広く活用されているものです。一見すると難しく思えるかもしれませんが、今回の記事のように具体例に当てはめてみるとすごく理解しやすくなります。
標準偏差をしっかりと理解してしまえば、他の統計学の用語も理解しやすくなります。標準偏差の活用を当たり前にするために、日々の生活や仕事で「標準偏差はどうなっているかな?」と考える習慣を是非つけてみてください。
標準偏差を理解出来たら次は重回帰分析にトライしてみるのもいいかもしれません。
データの管理・活用でお困りの場合はデータビズラボへお問い合わせください。
状況やニーズに合わせた様々なサポートをご提供いたします。





めちゃくちゃ分かりやすい説明でした!データの分析はオンライン授業であまり分からない分野でったので助かりました!
大変わかりやすい記事で参考になりました。
1点教えて頂きたいのですが、数量規模の違うもの同士を比較する際はどう考えればよいですか?
例えばですが、上記の株式の例で言いますと、
1,000円の株と10,000円の株では、標準偏差が大きく異なることになりますか?
その場合、どちらがより値動きが小さい/大きいと判断できますでしょうか?
ラーメンの例も同様です。
200gを1袋で販売する製麺所と400gを1袋で販売する製麺所においては、
これも標準偏差が大きく異なりますでしょうか?その場合、どちらがより
安定した1袋を作る能力があると判断できますでしょうか?
ご質問ありがとうございます。
仰る通り、数量規模が近いものだけでなく、規模が異なるものについても標準偏差を用いて業績比較することは可能です。以下、株価を例にご回答させていただきます。
①1,000円の株と10,000円の株では、標準偏差が大きく異なることになりますか?
→数量規模に違いがあるからといって、標準偏差が必ずしも異なるとは限りません。株価に変化をもたらす要因は株価の数量規模だけでなく、企業規模・体制・業界・タイミングなど外部の様々なものが考えられるためです。
②その場合、どちらがより値動きが小さい/大きいと判断できますでしょうか?
→株価の大小にかかわらず、標準偏差が大きいものの方が値動きは大きいと判断できます。たとえば10,000円株企業の標準偏差が100円、1,000円株企業の標準偏差が200円であったなら、株価の小さい1,000円株企業の方が値動きは大きいと判断することになります。
とてもわかり易くて助かります!!高校のIAの教科書はこんなに詳しく書かれておらず混乱するので。
とってもわかりやすかったです。
Tabeauでの分布バンドの標準偏差の意味に悩んでいたところとてもよく理解できました。
驚異的に分かりやすい!子供の偏差値を気にするパパママと全ビジネスマンが理解すべきですね
これまでに聞いた解説の中で最もわかりやすかったです。ありがとうございました。
会社の研修でヒストグラムを学ぶことになり予習しています。
分散を行う意味から分からなかったくらいなのですが理解できました。
全体的にとても分かりやすかったです!ありがとうございます🙇♂️