
箱ひげ図とは、データのばらつきを視覚的に示してくれるグラフのことです。
「箱ひげ図」と聞くと、「名前だけは聞いたことあるけどうまく説明できない」という方も多いでしょう。実際、箱ひげ図は、散布図やヒストグラムと違い、感覚的にその特徴を掴みにくく、一度聞いただけではすぐにその見方を忘れてしまいがちです。
そこで、本記事では以下のような方々に向けて箱ひげ図について解説しています。
「箱ひげ図の見方を知りたい」
「参考書で箱ひげ図の見方を学んでもすぐに忘れてしまう」
「箱ひげ図の具体的なメリットを知りたい」
「箱ひげ図をどんな場面で使えるか知りたい」
箱ひげ図の見方やメリット、よくある質問とその回答を、もう二度と忘れないように分かりやすくご紹介します!
目次
1.箱ひげ図はデータの分布を視覚的に示してくれるグラフ形式
箱ひげ図(Box and Whisker Plot)とは文字通り「箱」と「ひげ」に模された図の組み合わせによって、俯瞰的にデータの分布を把握することが可能なグラフの一つです。
統計データ可視化を成功させる95のチェックリストをダウンロードする
2.箱ひげ図の見方:構成要素は最小値・最大値・四分位数・四分位範囲・外れ値の5つ
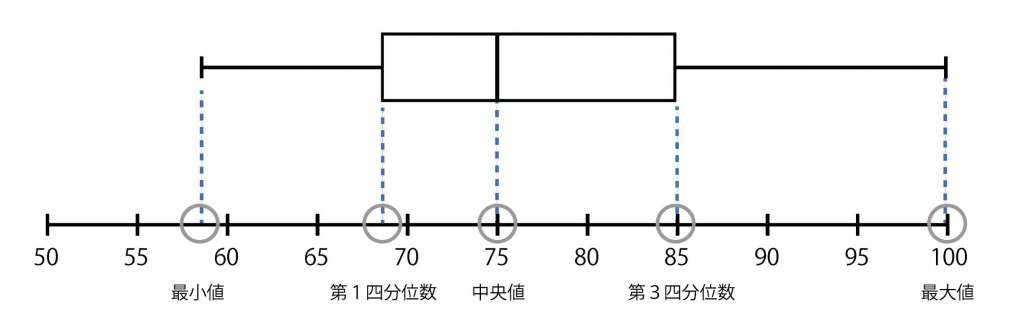
箱ひげ図を見る際に必ず知っておくべきことは、「箱ひげ図は、データのばらつきを把握するためにそれぞれの値を大きさ順に並べたグラフ」であるということです。そして、箱ひげ図が何を表しているのかをおさえるために見るべき指標が下記5つです。
- 最小値 (minimum)
- 最大値 (maximum)
- 四分位数(Quartile)
- 四分位範囲(IQR)
- 外れ値(Outlier)
箱ひげ図で対応する箇所はこのようになります。今回は聞きなじみのない四分位数・四分位範囲・外れ値に焦点を絞って1つずつ詳しく確認してみましょう。
2.1四分位数とはデータを4分割した値
四分位数とは、データを小さい方から均等に4分割(25%/50%/75%)したものです。この25%地点の値を第1四分位数、50%地点の値を第2四分位数(中央値)、75%地点の値を第3四分位数といいます。
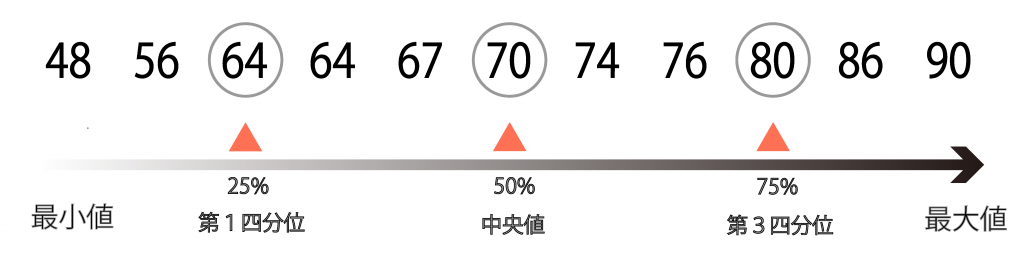
箱ひげ図では、データを小さい順に並べた際の50%地点である中央値だけでなく、25%地点である第1四分位数や75%地点である第3四分位数を求めることでデータのばらつきを把握します。
四分位数は以下の4ステップで求められます。
②中央値を求める
③データを「前半データ」と「後半データ」に分ける
④ 「前半データ」と「後半データ」でそれぞれ中央値を求める
STEP1:データを小さい順に並べる
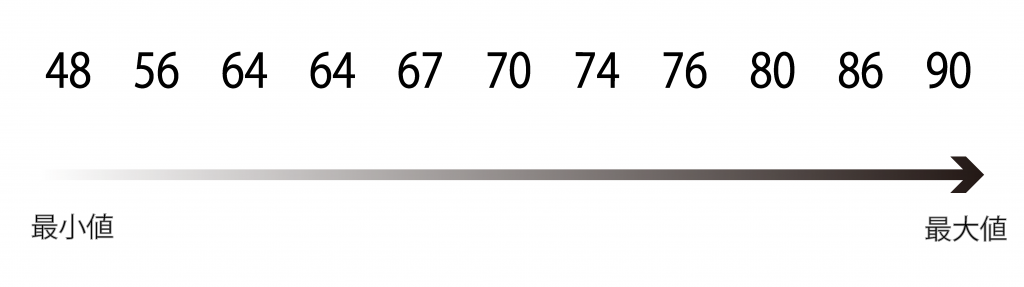
STEP2:中央値を求める
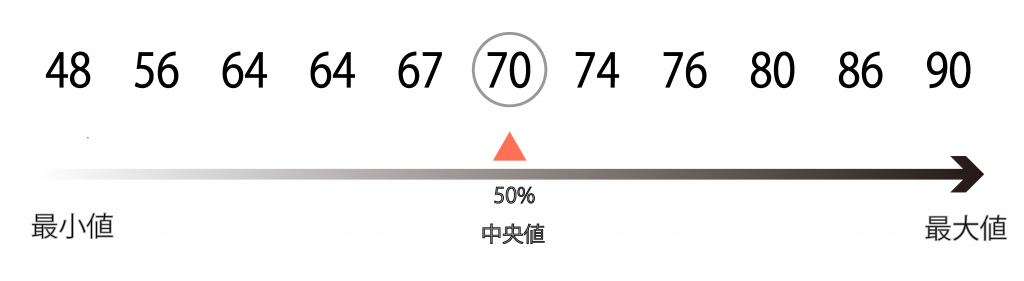
中央値は、データを大きさ順に並べた際に真ん中にくる値のことです。平均値は、データの値一つ一つを足し合わせ、データの個数で割った値のことです。
平均値や中央値以外にも基本となる統計量を知りたい方はぜひこちらの記事もご一読ください。
STEP3:データを「前半データ」と「後半データ」に分ける
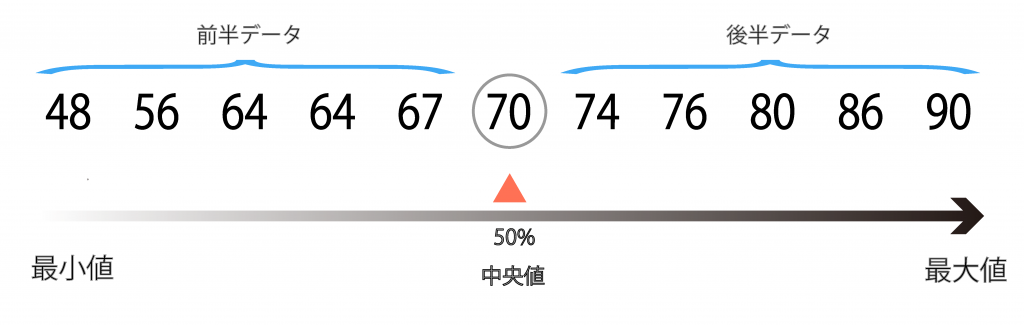
STEP4:「前半データ」と「後半データ」でそれぞれの中央値を求める
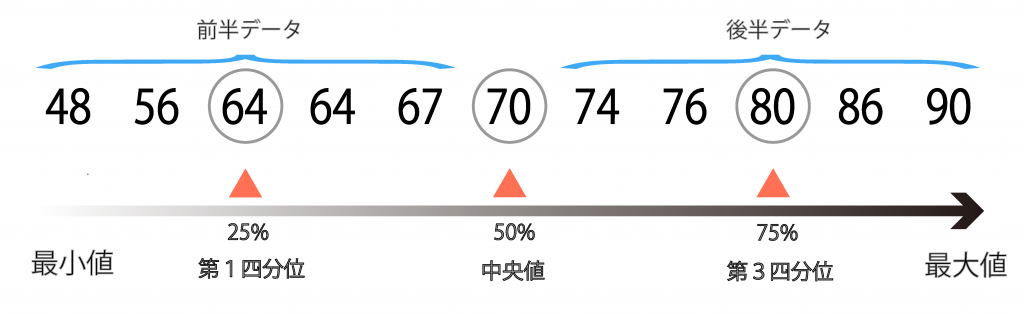
2.2四分位範囲とはデータの中央50%部分の範囲
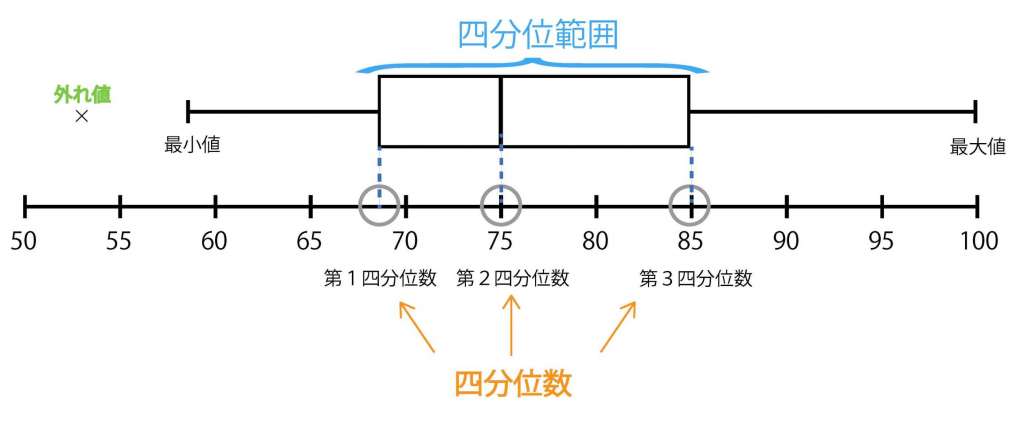
四分位範囲とは、データのちらばり具合を求めるもので、第1四分位数から第3四分位までの範囲(データの中央50%部分の範囲)のことを指します。
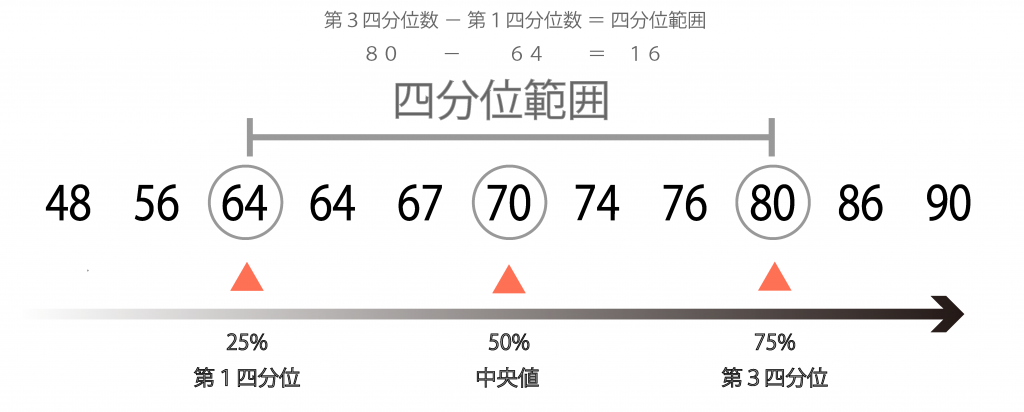
四分位範囲が大きければ大きいほど、データの散らばり具合は大きく、四分位範囲が小さければ小さいほどデータが密集していると言えます。今回の場合、第3四分位数の値は80とわかっているので、第1四分位数である64の差を求めることにより、四分位範囲は16と求めることができます。
2.3外れ値とは他の値から極端に離れている値
外れ値とは、データの中で極端に他の値からかけ離れている値のことを指します。通常、外れ値の値は大きすぎても小さすぎても最大・最小値として表さず、箱ひげ図の外に表します。外れ値を最大値または最小値とみなしてしまうと、ヒゲの長さが異常に長くなり、本来得たいデータのばらつきを適切に把握できなくなるためです。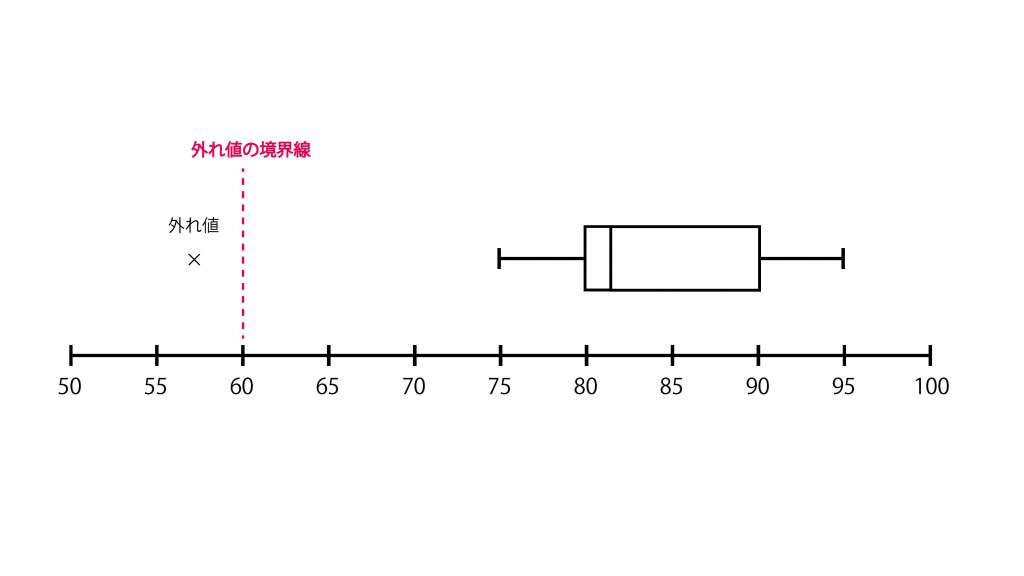
- 外れ値とみなされる値
「第3四分位数+四分位範囲×1.5」以上のデータ
「第1四分位数-四分位範囲×1.5」以下のデータ
四分位範囲を利用した外れ値の検出方法では、上記に当てはまるような明らかに他の数とかけ離れている値を外れ値とみなし、データセットから取り除くことができます。
3.箱ひげ図のメリット
箱ひげ図のメリットは2つあります。
- データのばらつきを把握できる
- 複数のデータを並べて比較できる
これらをおさえることで、箱ひげ図への理解が深まります。データのばらつき具合を把握する際によく使われるヒストグラムとの比較を交えながら紹介していくので、両者の違いも整理していきましょう。
3.1データのばらつきを把握できる
箱ひげ図はデータを4等分する四分位数を基に作成されます。この四分位数を基にした、箱とヒゲが表す幅によってデータのばらつきを把握することができます。
箱ひげ図は以下5つの指標を同時に表しています。
- 最小値(minimum)…データの中で最も小さな値 箱ひげ図における下髭の部分
- 第1四分位数(25th Percentile) …データを小さい順に並べた際の全体で25%に位置する値
- 中央値(median)…データにおいて真ん中の値 データの個数が偶数の時は、真ん中2つの平均の値
- 第3四分位数(75th Percentile) …データを小さい順に並べた際の全体で75%に位置する値
- 最大値(maximum)…データの中で最も大きな値 箱ひげ図における上髭の部分
参考:『誰もが知っておくべき「基本統計量」の基礎知識をわかりやすく解説』
これら5つの指標を同時に表してくれることの具体的な利点はどこにあるのか掴むために例をみていきましょう。
下記の表は、あるクラスの生徒30人おける身長の値をまとめたものです。
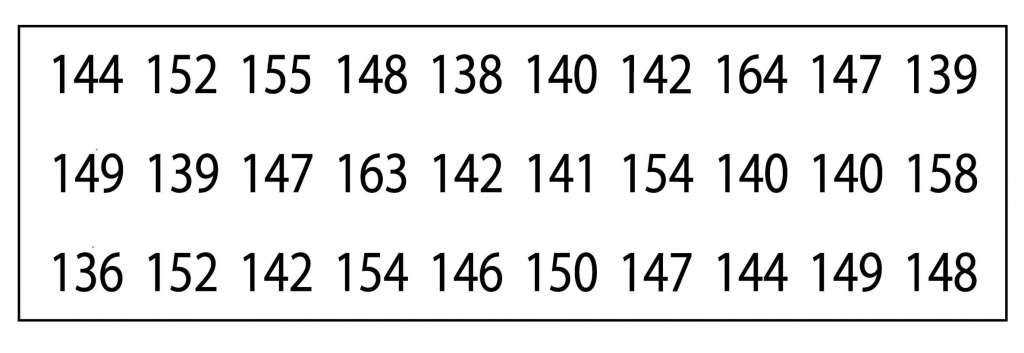
この表を見るだけでは、最も背の高い(低い)人は何cmで、中間に位置する身長は何センチなのかを掴むことはできません。
では、ヒストグラムではいかがでしょうか。
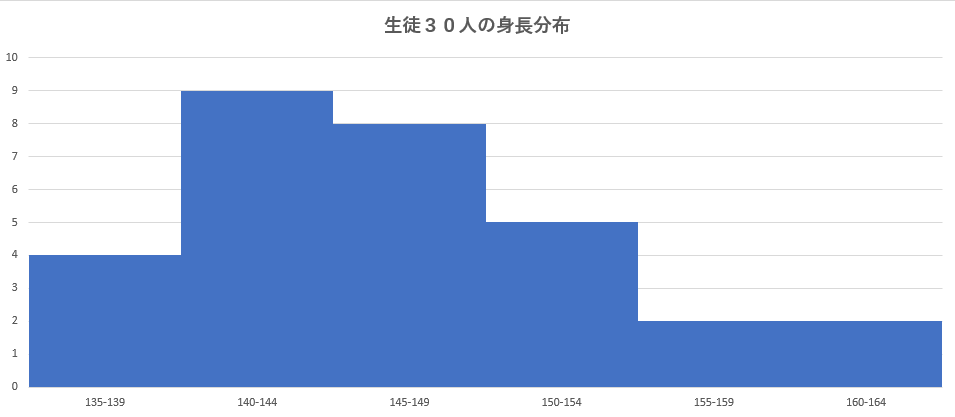
このように、ヒストグラムを用いても分かるのは身長の偏り具合のみで、クラスで最も背の高い(低い)人は何cmで、クラスで中間に位置する身長は掴めません。
そこで箱ひげ図をみていきましょう。
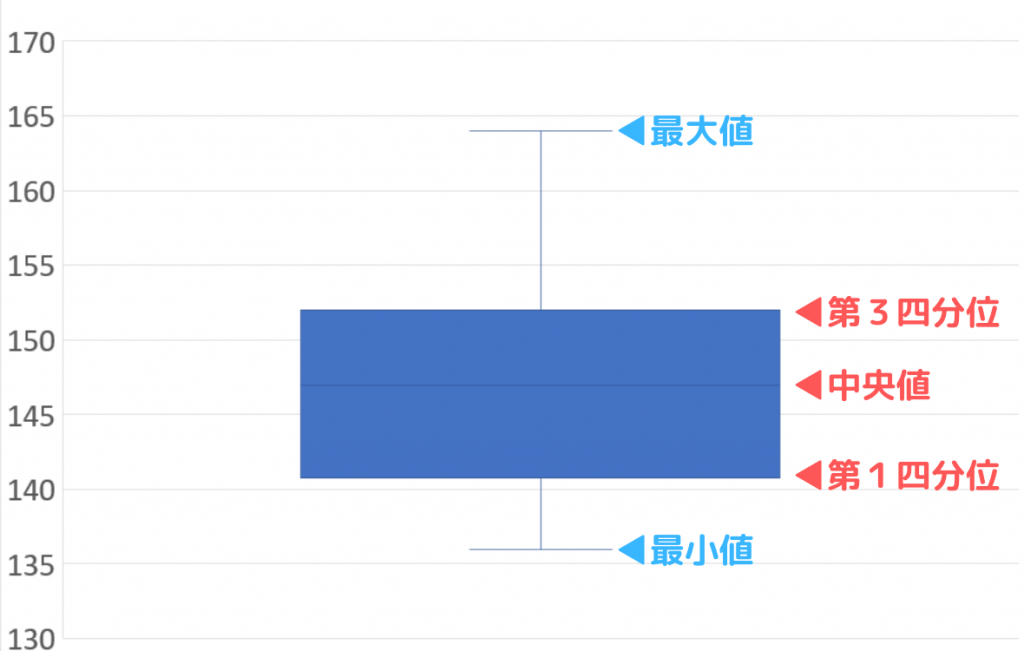
このように、重要な指標がこのように全て一瞬でわかるのが、箱ひげ図です。今回であれば、生徒30人のうちの多くが約145㎝周辺に位置している一方で最も背の高い生徒の身長は約164㎝あり、最も背の低い生徒は約136㎝であるとわかります。
箱ひげ図の形状がヒストグラムではどのように表されるのか気になる方も多いと思うので、ヒストグラムも併せて紹介します。
箱が狭くヒゲが長い場合
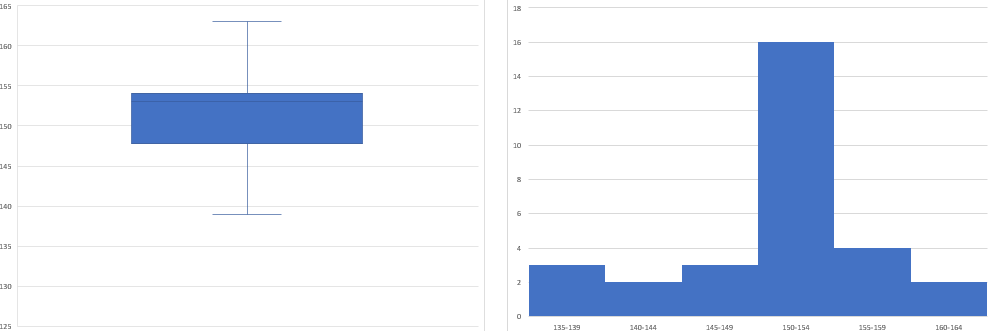
このように箱が狭く髭が長い図では、中央部分にデータが密集していることが掴めます。
②箱が広くヒゲが短い場合
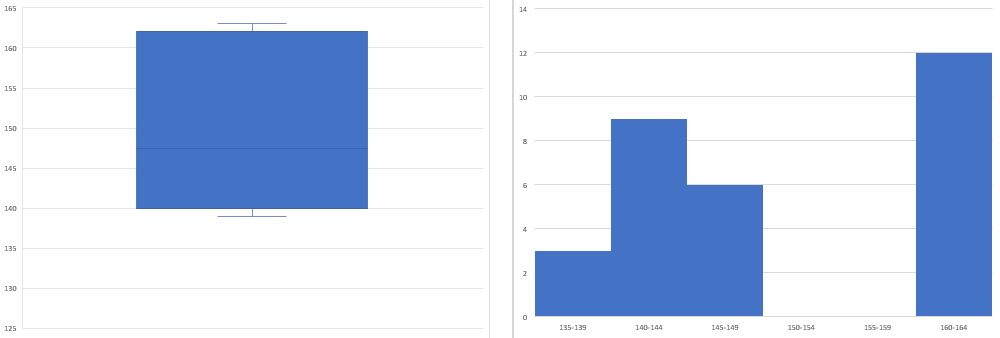
次に箱が広くヒゲが短い場合、中央にデータが密集している時と比べ、データが二極化している可能性が高いと言えます。
③箱が上下(左右)どちらかに偏っている場合
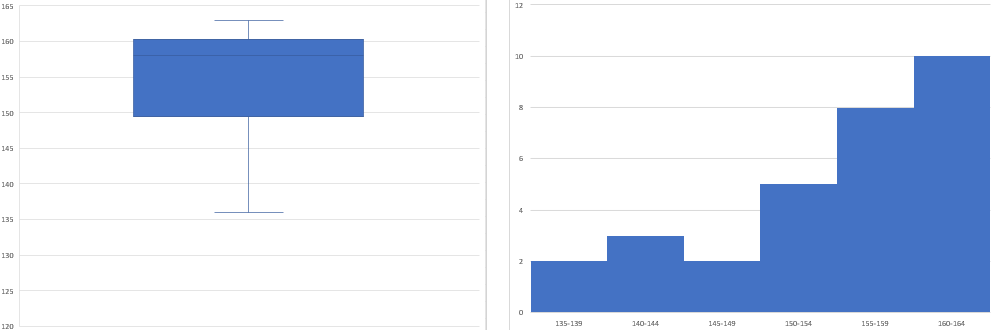
また、箱に偏りがある場合、偏っている側にデータが密集しています。
2.2複数のデータの分布をコンパクトに比較できる
また、箱ひげ図は複数のデータを並べて比較できます。
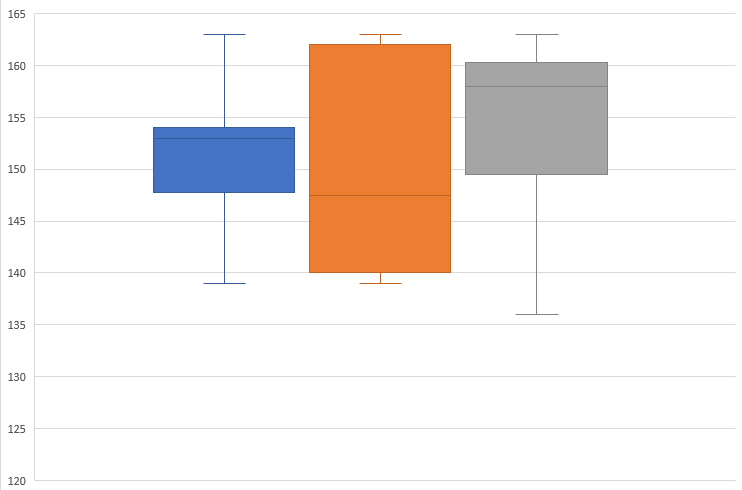
こちらは3つの箱ひげ図を並べたものになります。箱ひげ図はコンパクトなグラフ形式に多くの情報が詰まっており、その意味で比較がしやすいです。この図をみると、オレンジの箱ひげ図はばらつきが大きく、青色の箱ひげ図はばらつきが小さいというような比較が簡単にできます。
2020年度のセンター試験では、下記のような問題も出題されました。
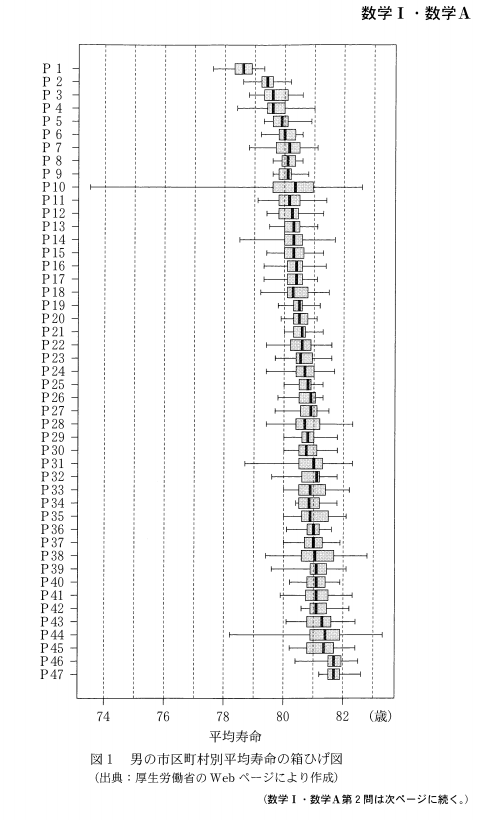
(出典:令和2年度センター試験 数学ⅠA)
ちなみに、上述の箱ひげ図をヒストグラムで表現すると、以下のようになります。

複数のデータを比較する必要がある場合は箱ひげ図を用いることが多いです。逆に単一データにおける「ばらつき具合」を詳細に掴みたい場合はヒストグラムを使います。
もちろん目的に応じて箱ひげ図とヒストグラムを使い分けることは可能ですが、データの特徴を深く掴むためには両方併せて使うことをおすすめします。
4.Excelでの箱ひげ図の作成方法
箱ひげ図はExcelにて以下の5ステップで簡単に作成することが可能です。
STEP1:データセットの用意
データセットを用意します。
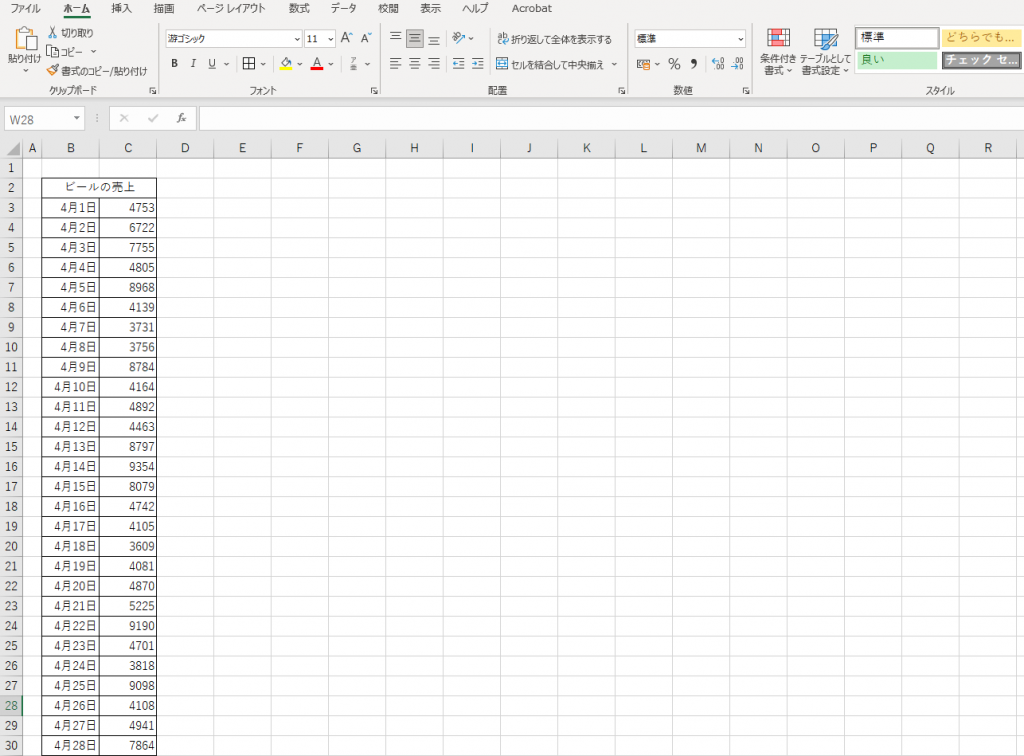
STEP2:範囲の選択
次に範囲を選択します。
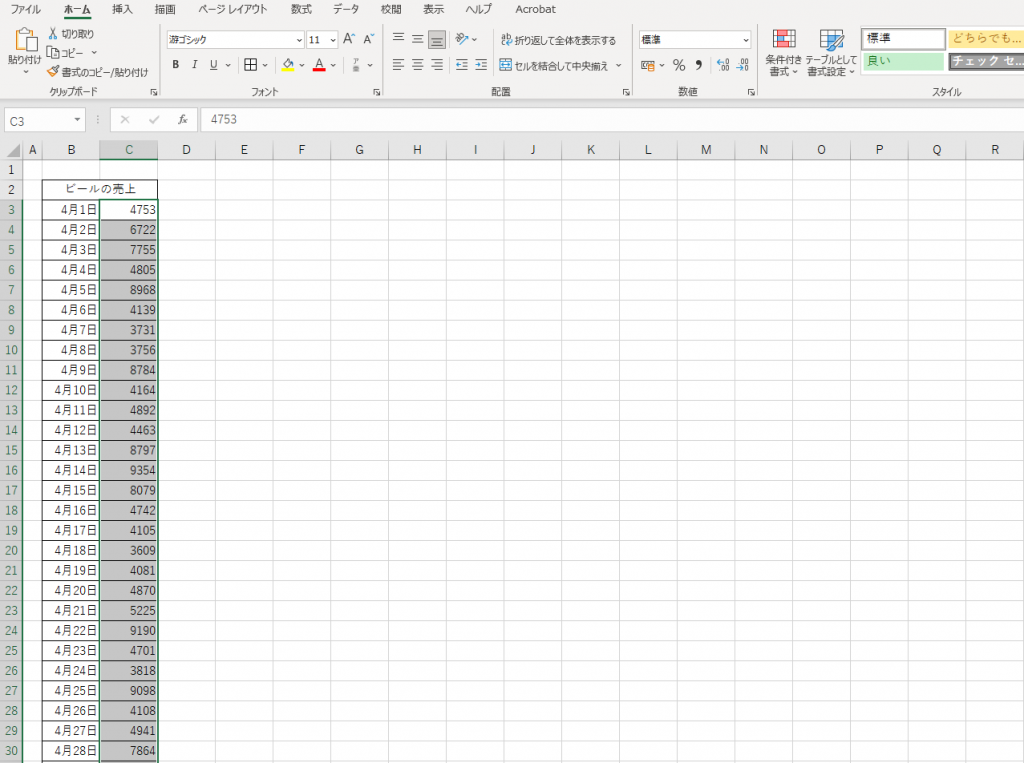
STEP3:挿入をクリックし、箱ひげ図を挿入
挿入をクリックし、箱ひげ図を挿入します。
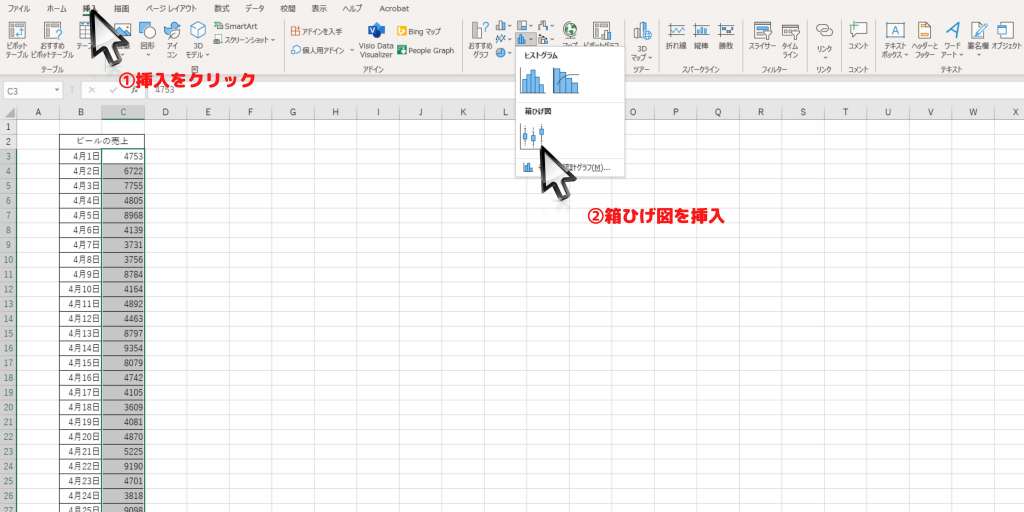
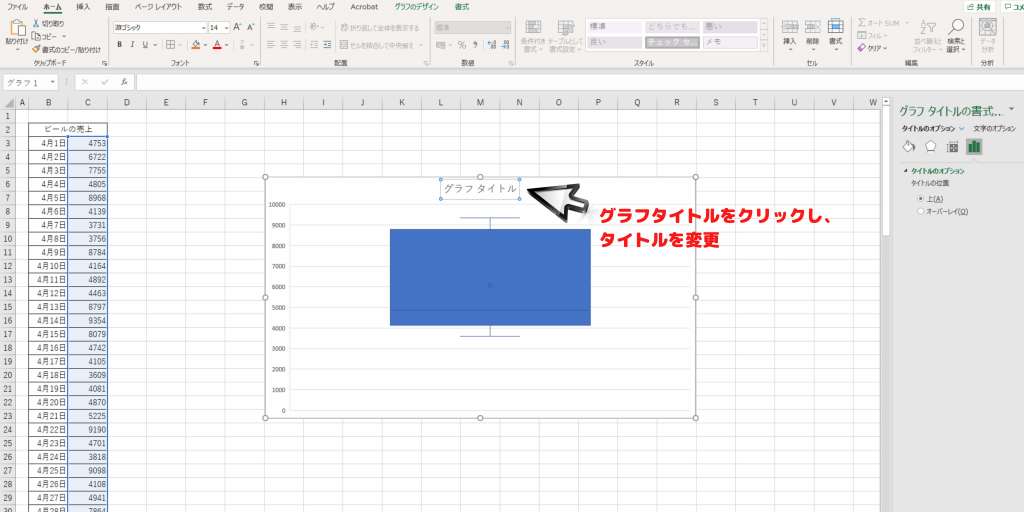
STEP4:タイトルの設定
箱ひげ図を挿入したら、タイトルを設定していきます。
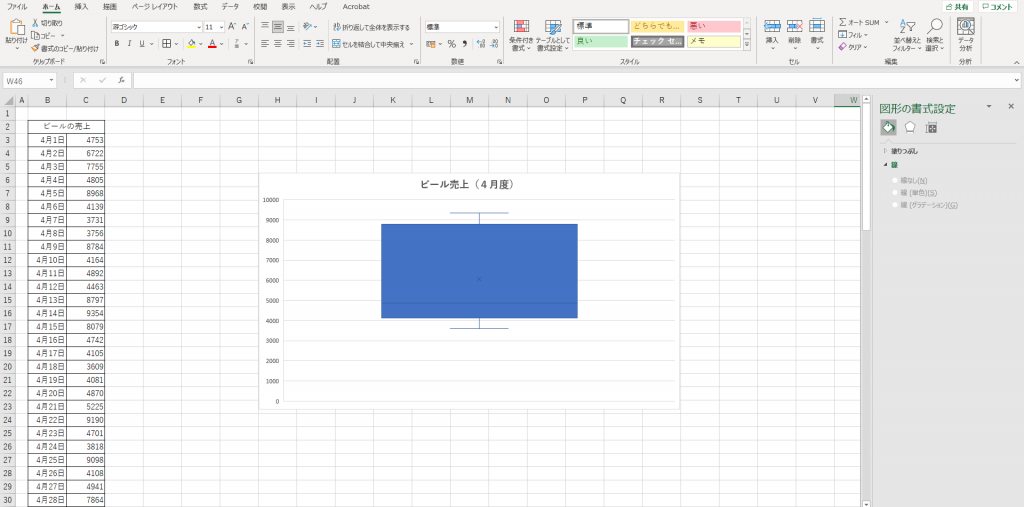
完成
完成形がこちらになります。
5.箱ひげ図の作成方法 (Python)
箱ひげ図は他のツールでも作成可能です。今回はPythonで作成したものをご紹介いたします。

Pythonを使って箱ひげ図を作成すると一度型を作ってしまえば後は変数を設定するだけで簡単に複数作成可能なためとても便利です。
Pythonを使ったデータ分析に興味がある方はこちらの記事もご一読ください。
おわりに
今回は、意外とすぐに忘れてしまいがちな箱ひげ図について概要やメリット、作成方法までご紹介いたしました。
本記事を読むことで箱ひげ図への理解が定着することに繋がれば幸いです。
データの管理・活用でお困りの場合はデータビズラボへお問い合わせください。
データビズラボでは状況やニーズに合わせた様々なサポートをご提供いたします。
また箱ひげ図を学んでみて「データから何か示唆を得ること」に魅力を感じた方はデータ分析に挑戦してみるのもいいかもしれません。データ分析を学習する上でおすすめの本をこちらで紹介しているので良ければ是非ご一読ください。





コメント