変動係数とは？定義からエクセルでの求め方までわかりやすく解説！

変動係数とは標準偏差を平均値で割った値のことです。標準偏差と同様にデータのばらつきを把握できる指標の1つになります。

参考：『標準偏差とは？意味から求め方、分散との違いまでわかりやすく解説』

変動係数は統計学の基本的な指標ですが、「なぜ変動係数を求める必要があるのか」「どのように変動係数を求めればいいか忘れてしまう」という方も多くいらっしゃるのではないでしょうか。

統計検定3級の出題範囲でもある「変動係数」について、本記事では、図解を用いて分かりやすく簡単に解説いたします。

1.変動係数とは、標準偏差を平均値で割った値である

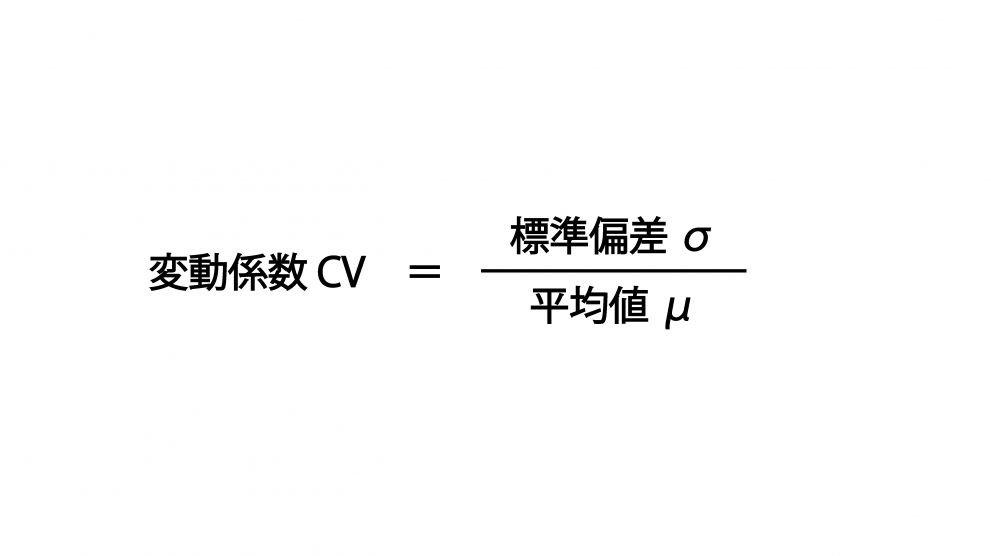
変動係数とは標準偏差を平均値で割った値であり、データ同士のばらつきを相対的に評価するための値のことです。英語の「Coefficient of Variation」の頭文字を取って「CV」と表記されます。

式にするとこのようになります。

1.1.変動係数によって異なるデータのばらつきを比較できる

変動係数を求める理由は、異なるデータ同士を比較できるようにするためです。

変動係数を求める際に使う標準偏差はデータのばらつきを掴むことができる指標ですが、異なるデータ同士を比較して相対的にどちらのばらつき具合が大きいかを評価することはできません。

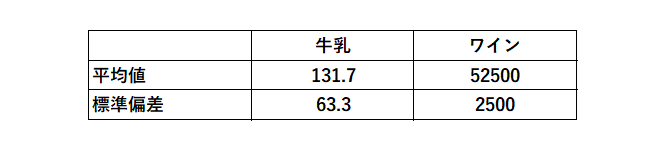
例えば、下図はスーパーにある牛乳とワインのそれぞれの値段を表し、その平均値と標準偏差を表にしたものになります。

牛乳とワインの標準偏差の値を見てみると、ワインのばらつきが大きいことがわかります。

しかしながら、これは単にワインの値段が牛乳よりも高いためです。よって両者のばらつきを相対的に比較するためには、それぞれの標準偏差を平均値で割るという手順が必要になります。次の章でそれぞれの変動係数を求め、両者のばらつきを比較していきましょう。

1.2.変動係数の求め方と解釈の仕方

冒頭でもお伝えしましたが、変動係数は標準偏差を平均値で割ることで求めます。牛乳とワインのそれぞれの変動係数は以下の式で求めることができます。

値の大きさから、感覚的にはワインのばらつきの方が大きいと判断してしまいそうな牛乳とワインの比較も、値の大きさによる影響をなくし、相対的に比較してみると牛乳の値段のばらつきの方が大きいということがわかります。

変動係数の値が実際にどれほどばらつきがあるか判断するのは困難ですが、一般的に変動係数が1を超えている場合、ばらつきが非常に大きいデータであると判断できます。具体的にいうと、データの中に外れ値がある可能性が高いといえます。しかし一方で、顧客の購買データやそもそもデータ量が多いデータに関してはばらつきが大きくなるのは自然なことなので、「変動係数が1を超える＝データがおかしい」と断定することはできません。

2.時系列データを用いて変動係数を活用する

変動係数の推移を見ることで、どの時期にどのデータの散らばりが大きかったのかを比較することができます。

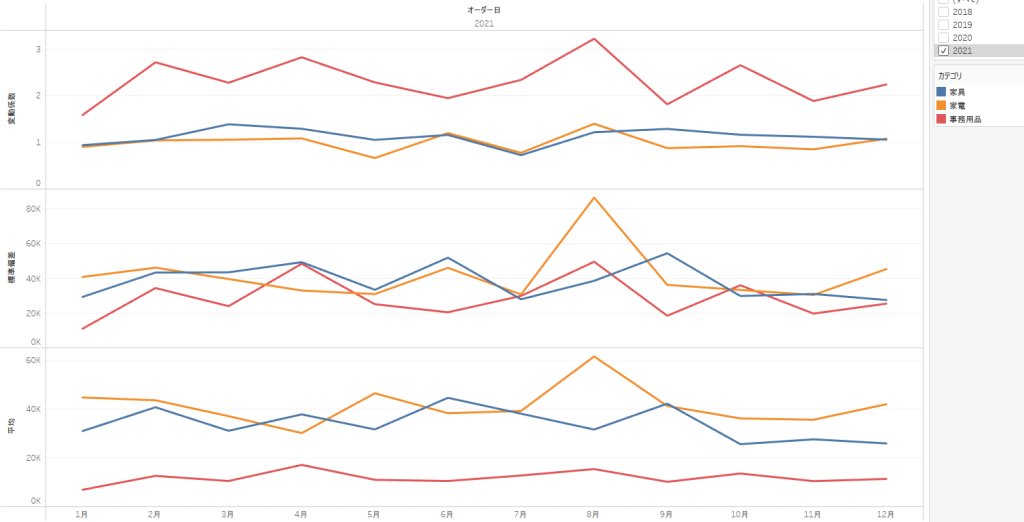
下の図はTableauで作ったもので、家具と家電、事務用品の売り上げの変動係数と標準偏差、平均値それぞれの推移を示したものです。購買データで、かつデータ量が膨大であるため、変動係数はかなり大きく出ています。

標準偏差で比較すると事務用品の売り上げのばらつきは小さく見えますが、変動係数で比較することでばらつきそのものは1番大きいとわかります。標準偏差はあくまで標準的な平均と各データの差を表すものなので、異なるデータ間での比較には向いていないことがわかります。

この変動係数の数値から、例えば以下のような仮説を立てることができます。

• 事務用品は主力商品でないため、そもそも売り上げが低い
• ペン1本から、事業所向けの膨大な発注にまで対応しているため、一番ばらつきが大きく、大型注文が入った月とそうでない月に差がある
• 家電や家具はばらつきが少ないため、ある程度決まった在庫を持ちやすい

3.よく似た標準化との違いは？

変動係数についてここまで学んだ方の多くが標準化と似ていることに気付いたのではないでしょうか。標準化とは、平均が0、分散が1となるようデータを変換することであり、変動係数と同じく異なるデータの比較を行うために用います。しかしながら、変動係数と標準化では使用する場面が明確に異なります。

変動係数は異なるデータセット間のばらつきを比較する際に用いられますが、標準化は各データの値を揃え比較する際に用いられます。

標準化は、英語で「Standardization」と呼び、式にするとこのようになります。

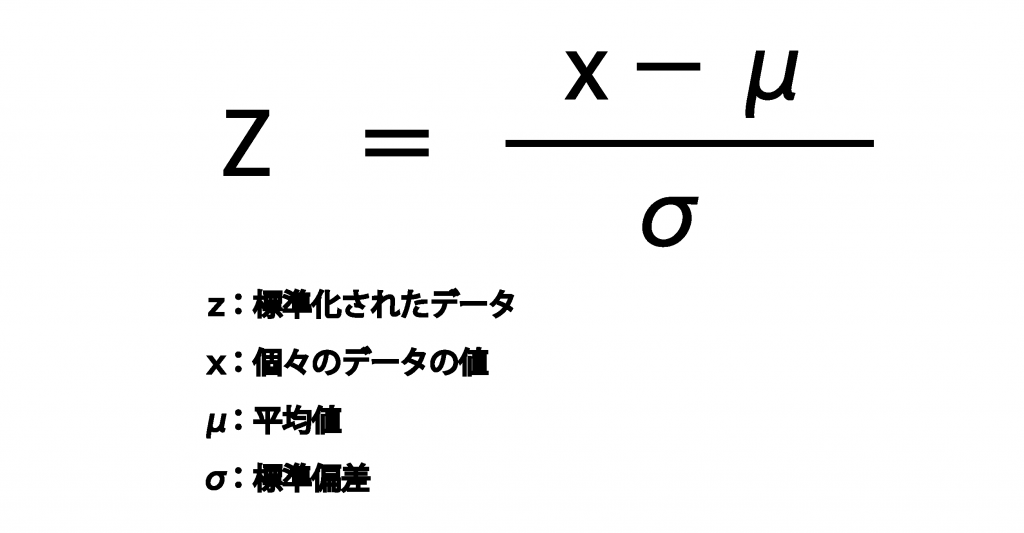
4.エクセルでの変動係数の求め方

最後にエクセルでの求め方について紹介していきます。

変動係数のエクセルでの求め方は4ステップです。

実際に詳しくみていきましょう。

STEP1：データセットの準備

まずはデータセットを用意します。今回は、国語のテストの点数における変動係数を求めていきます。

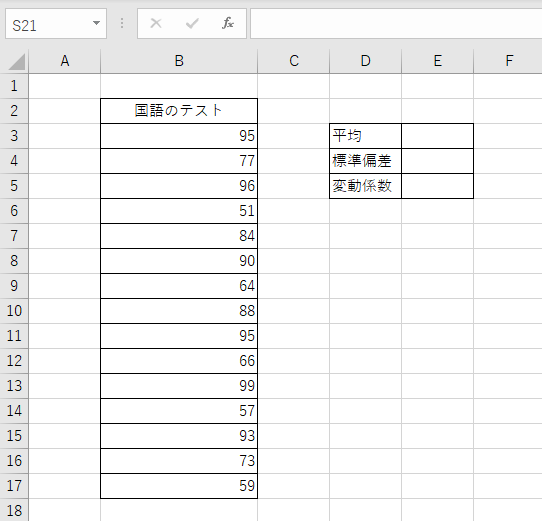
STEP2：平均を求める

データセットを用意したら、まずはAVERAGE関数で平均を求めていきます。

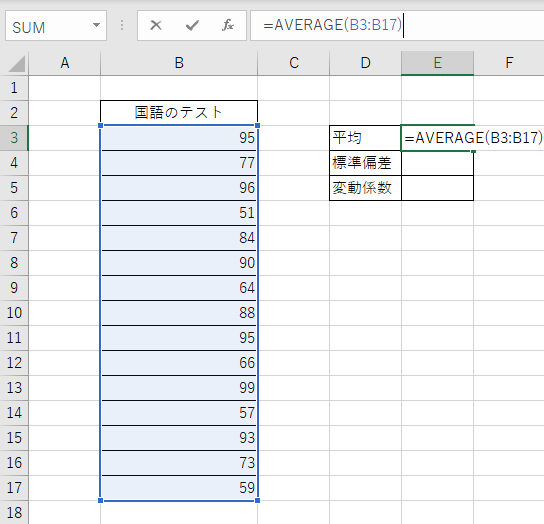
STEP3：標準偏差を求める

次にSTEDEV.P関数で標準偏差を求めます。

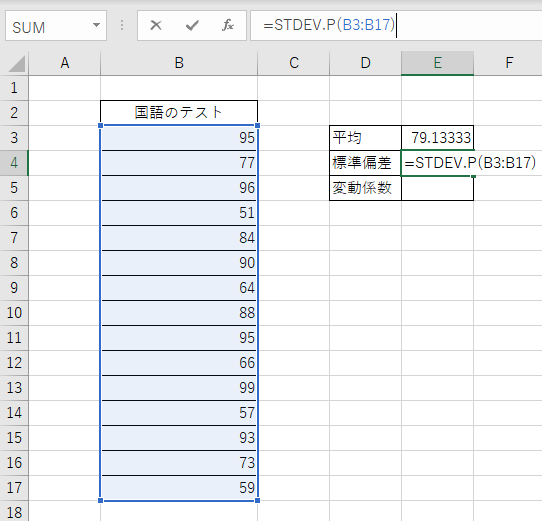
STEP4：変動係数を求める

最後に、変動係数は、STDEVP(データ範囲)/AVERAGE(データ範囲)で求めることができるため、下記の式で求めていきます。

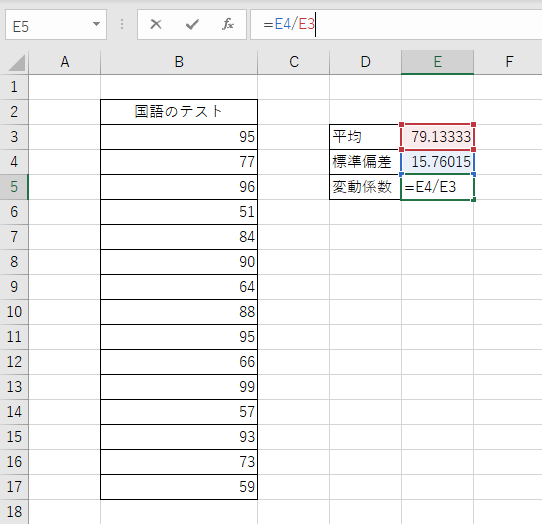
完成

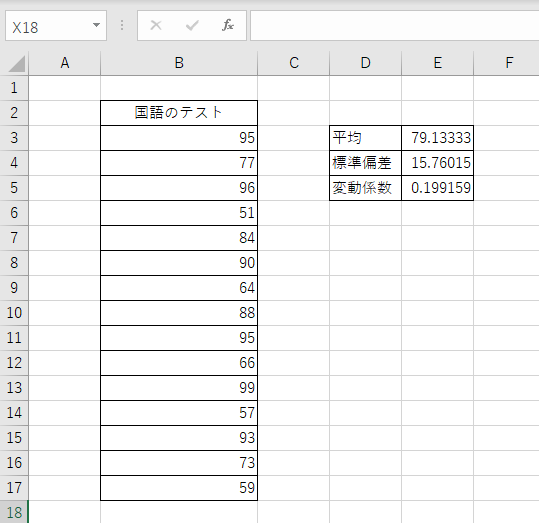
変動係数の求め方は以上になります。今回は国語のテストにおける点数の変動係数は0.199という値が得られました。

まとめ

今回は統計検定でも出題される変動係数の定義や標準化との違い、エクセルでの求め方まで簡単にご紹介いたしました。

統計検定を受ける予定の方も、そうでない方も本記事を読んで統計学に関する知識をより深めていただけたなら幸いです。最後に統計検定の受験を検討されている方に向けて以下の記事をご紹介いたします。ぜひご活用ください。

【統計検定3級対策】出題範囲、勉強時間の目安や難易度までわかりやすく解説

【統計検定2級対策】難易度や出題範囲を解説