
過学習とは、「コンピューターが手元にあるデータから学習しすぎた結果、予測がうまくできなくなってしまった」という状態です。
過学習を理解し、対処法を知っておくことはデータ分析を行う上で非常に重要です。
- なぜ過学習になるのか
- どうすれば作成した予測モデルが過学習になっているかわかるのか
- 過学習にならないために、どのような対策ができるのか
本記事では上記のポイントについて、機械学習を学び始めたばかりの方向けにわかりやすく解説いたします。
第1章 過学習とは予測がうまくできなくなった状態である
1-1. 過学習を理解するための前提知識
過学習は、「過学習」という言葉の中にある「学習」と、手元にあるデータから予測する際に構築する予測モデルについて知っておくことでスムーズに理解できます。
過学習の学習とは
過学習の「学習」は一般的に言う学習とは違い、コンピューターが今手元にあるデータから何かしらのパターンや規則性を見つける作業です。
予測モデルとは
機械が見つけてくれたパターンを、未知のデータに当てはめて予測させることです。
1-2. 過学習の具体例
具体例として、「あるクラスの点数の分布から学年全体の点数の分布を予測するモデル」について考えてみましょう。
国語と算数のテスト(100点満点)をそれぞれ縦軸と横軸に取って散布図を作成し、コンピューターが学習して見つけてくれたパターンを2つ、モデルとして書き込みます。2つの予測モデルのうち過学習になっているモデル(曲線)はどちらか、クイズ感覚で考えてみてください。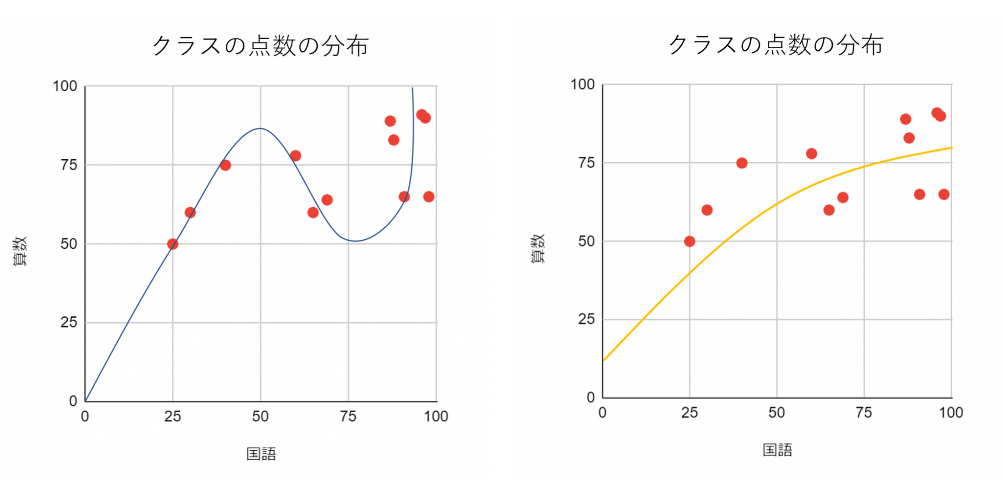
モデルとしてより優れているのはどちらだと思いますか?一見、左の図の方があてはまりがよさそうに見えませんか?
では、正解発表です。予測したかったデータのサンプルもこの図に足してみましょう。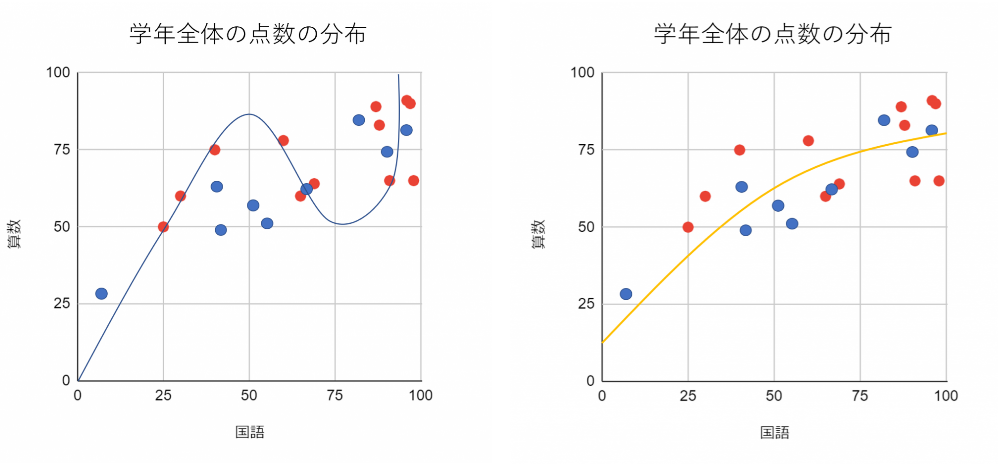
このように見ると、明らかに右のモデルの方が予測したかったデータに対してもよくフィットしてますよね。過学習になっている左のモデルでは、手元のデータにフィットしすぎて予測したいデータに全くあてはまらない状態になってしまいました。
このように、データ全体の傾向をつかめずデータの1つ1つの要素にフィットしすぎていると過学習に陥ります。
1-3. 過学習に陥っている予測モデルの問題点はデータ全体の傾向がつかめていないことである
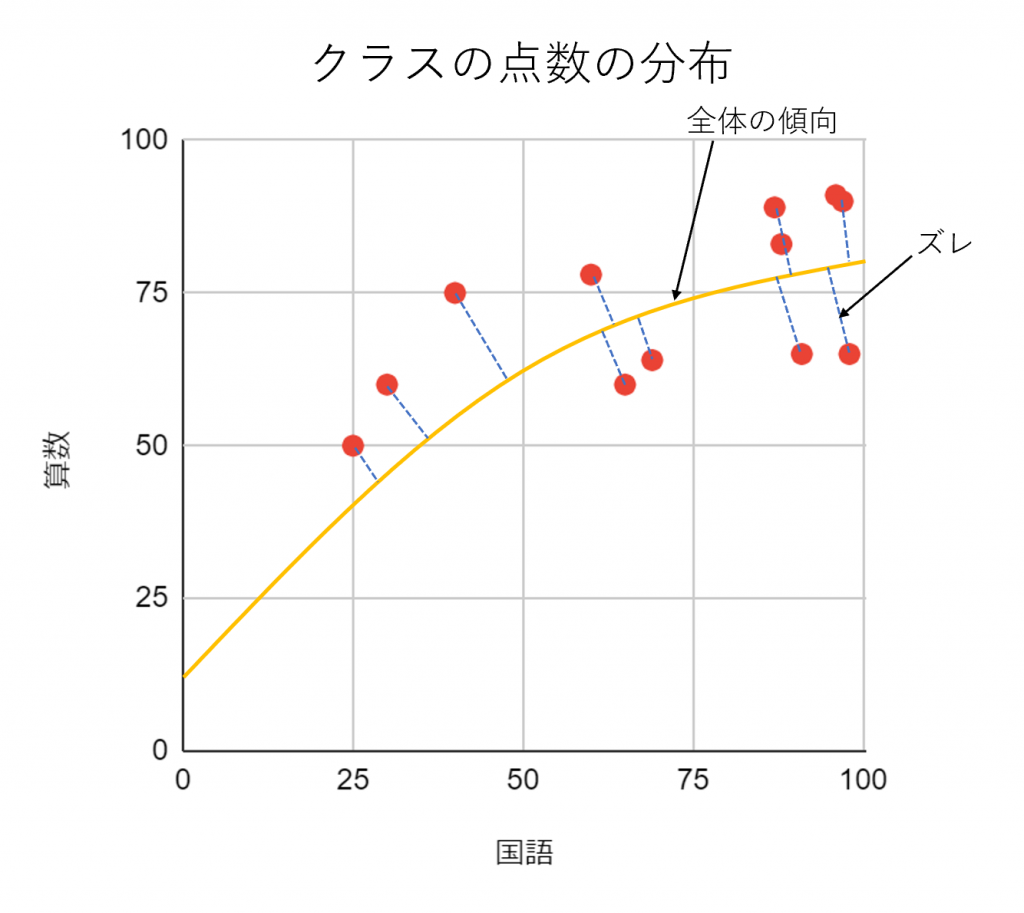
過学習に陥っている予測モデルは、下の図のようにデータ全体の傾向がつかめずに1つ1つの要素にフィットしすぎている傾向にあります。
データ1つ1つを記述することはできていますが、このデータが“全体として”どういう傾向を持っているのかこのモデルでははっきりしません。このようなモデルでは元データにおける適合度と、テストデータにおける予測精度に著しく差が出てしまいます。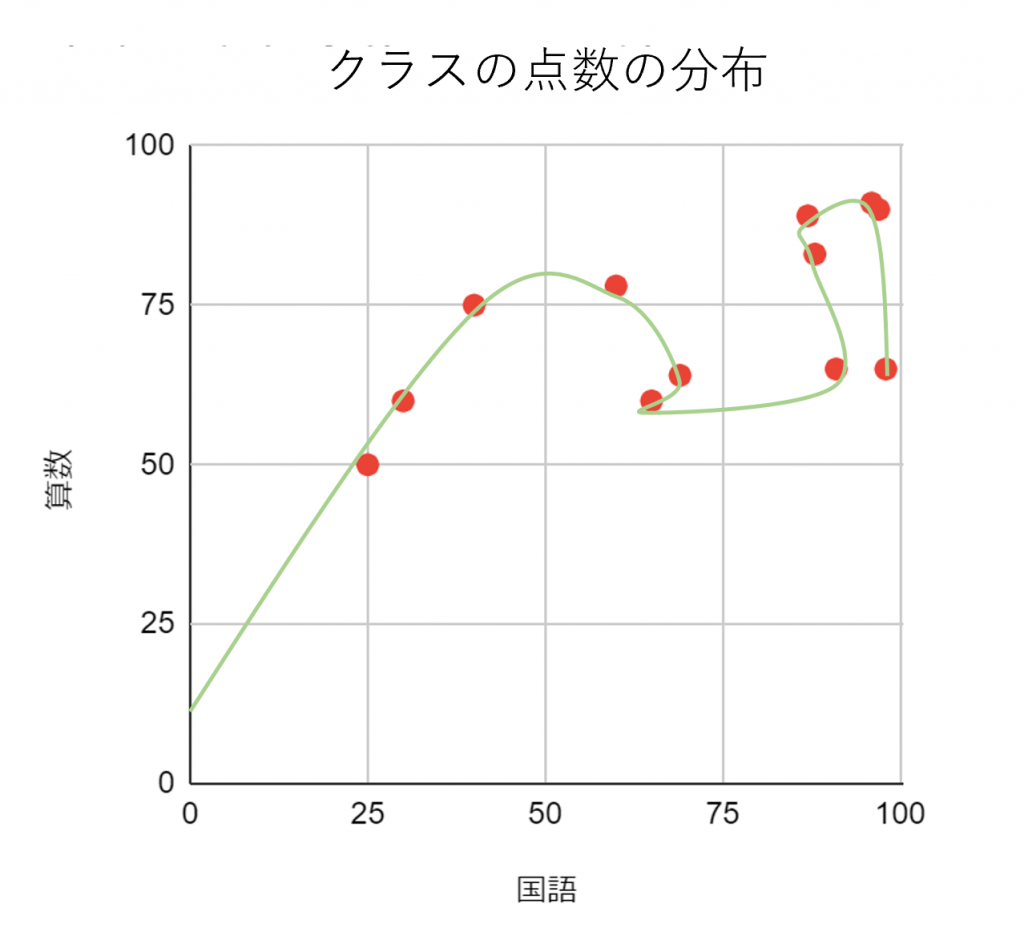
データ全体の傾向がつかめなくなる理由は、データの要素1つ1つがもっている”ズレ”に予測モデルが適合してしまうためです。この結果、予測モデルはいびつな形になり、予測に使えなくなってしまいます。予測モデルとはこの図における黄色い曲線のようにデータのパターンや規則性を読み取って記述するものです。
1-4. 過学習に気づけないと予測モデルが改善できない
過学習に気づけないと予測モデルをアップデートできずに中途半端なモデルばかりを量産することになります。
過学習に気づけない悪循環
予測モデルを作る→目の前にあるデータに集中して精度を上げる→過学習になっていることに気づかずに自己満足する→別の分析手法の勉強にとりかかる→同じように過学習になっていることに気づかない→…
いつの間にか過学習になったモデルばかりがあふれたゴミ箱を抱えることになります。

過学習の悪循環にはまらないように
まずは自分の作ったモデルが過学習になっていると気づくことがとても大事です。そして、その次のステップとしてなぜ過学習になっているのか原因を突き止め、どうやって解決すればいいかを考えることができます。
第2章 過学習に気づくために
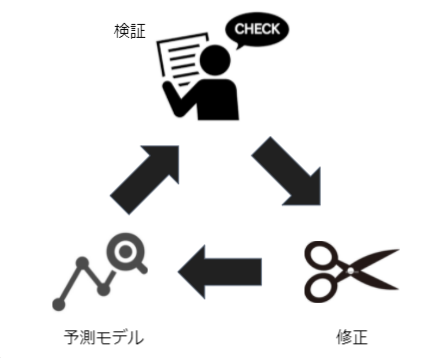
中途半端なモデルを量産する悪循環にはまらないように、「モデルを作ってみる→検証する→改善する→同じ手法でよりよいモデルを作る」というサイクルを回して過学習に気づき、改善していくことが重要です。
2-1. 予め訓練データと検証データ、テストデータに分けておく
訓練データと検証データ、テストデータにはそれぞれ役割があり、これらを準備することで予測モデルを作ってから検証することができます。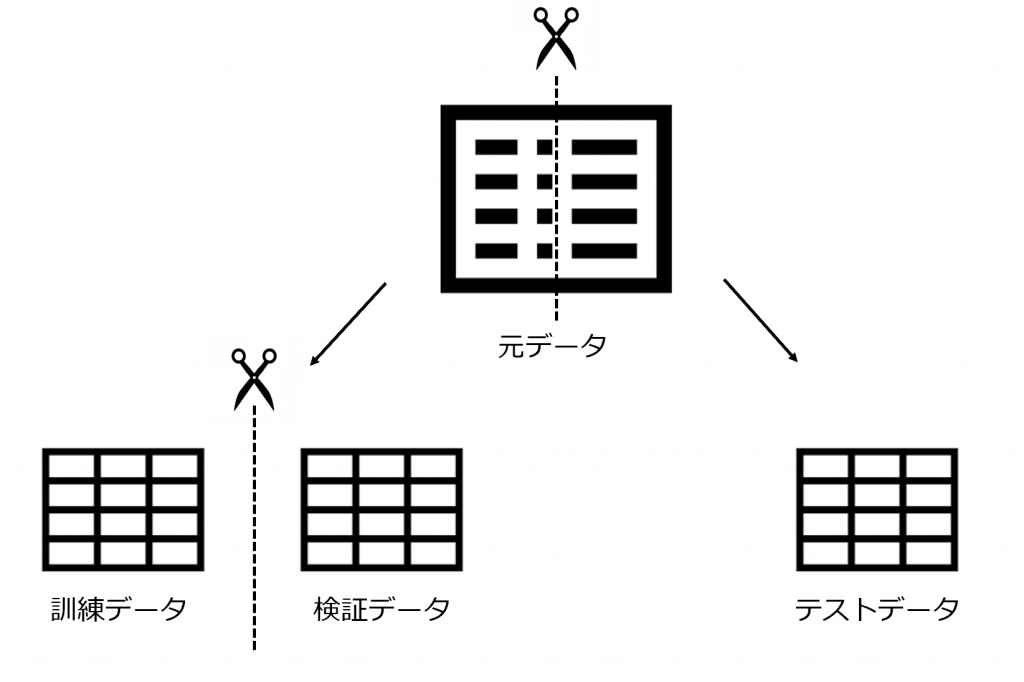
- 訓練データ:モデル作成するために使うデータ
- 検証データ:モデルの精度を検証していくためのデータ
- テストデータ:未知のデータの代わりに最終的に精度を確かめるためのデータ
モデルを鍛える訓練データ
訓練データの目的は予測モデルを作ることです。
試行錯誤のために使う検証データ
検証データはうまくいかない場合の原因究明、試行錯誤のために使うものです。訓練データと検証データを行き来しながらモデルの精度を上げていきます。
また、この後に説明する学習曲線や交差検証、検証曲線でも検証データが必要になります。
テストデータ(最後の関門)
テストデータは訓練データと検証データを使って練り上げた予測モデルを最終的にテストするためのデータです。検証データとテストデータのダブルチェックを経て使えることが立証された予測モデルが実際の現場で使われます。
大学入試で例えると検証データは何度も受ける模試のようなイメージ、テストデータは本番の入学試験のようなイメージです。
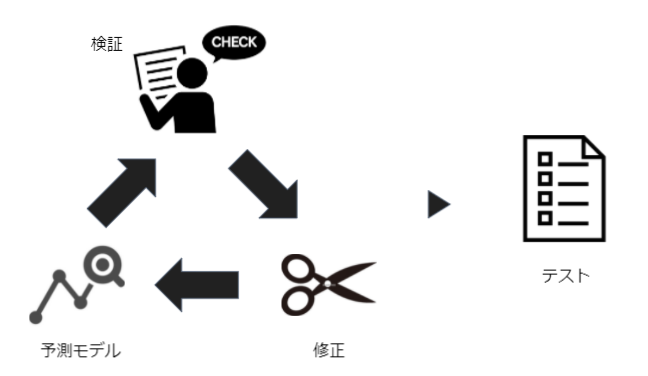
このように検証のプロセスを行っていく代表的な手法は2つあります。
- ホールドアウト法
- 交差検証法
2-2. ホールドアウト法による検証
ホールドアウト法とは訓練データと検証データ、テストデータを分割してモデルを作成する度に検証をはさみながら分析していく基礎的な手法です。
ホールドアウト法のメリット
メリットは実装が簡単なことと、コンピューターが計算する負担が少ないことです。
データ数が10万以上でコンピューターのスペックがあまり高くないときにはホールドアウト法が便利です。
ホールドアウト法の注意点
ホールドアウト法では、訓練データと検証データを1通りの分割しかしないので、データの分割がうまくいかずにデータの傾向に偏りが出てしまう場合があります。訓練データと検証データそれぞれのデータの傾向に違いがあると、当然訓練データから作成したモデルは検証データにうまくフィットせずに過学習と同じような結果が出ることになります。
基本統計量からデータの傾向を確認
基本的には2つのデータの平均値、中央値といったデータを代表する値や標準偏差などデータの散らばり具合を見て2つのデータが同じ傾向を持っているか判断しましょう。こうした値を基本統計量と呼びます。基本統計量についてくわしくはこちらの記事をご参照ください。
こちらの2つのデータの基本統計量を見ると全く違う傾向にあることがわかります。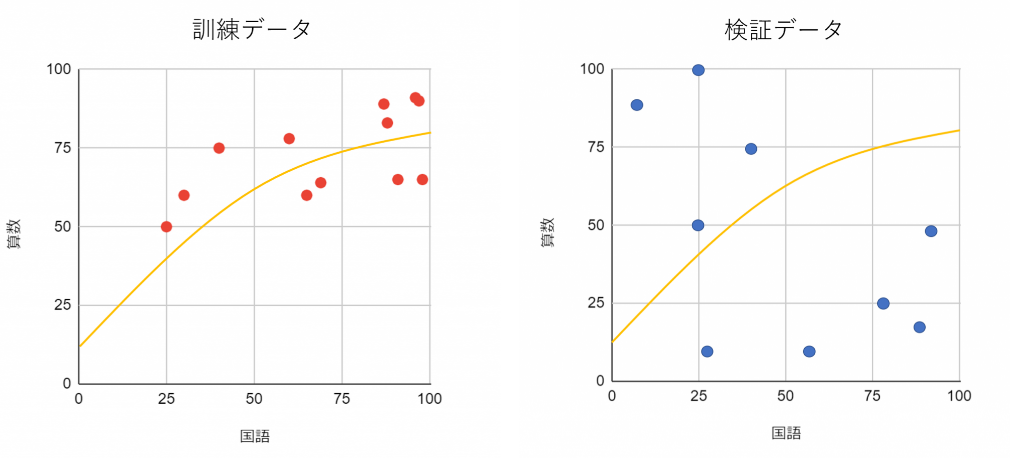
では次の2つのデータの基本統計量を見比べてみるとどうでしょうか。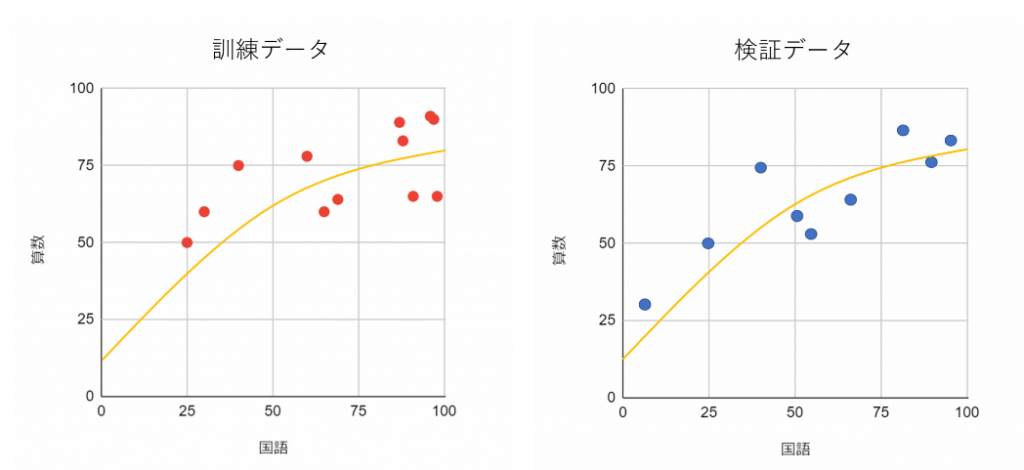
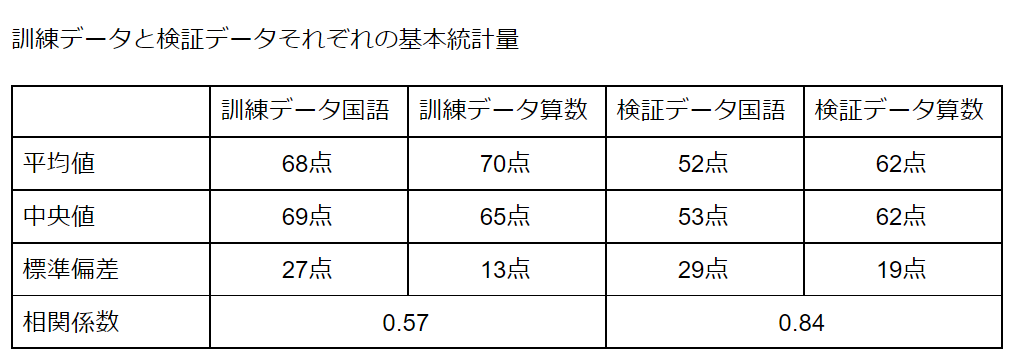
平均値や中央値には差がありますが、相関関係としては強さに差があるものの同じ正の相関があるようです。同じ傾向にあるデータだと言えるでしょう。
基本統計量の限界
データを分割する際に、あらかじめ平均値や相関係数が同じになるように設定するのも1つの方法です。ただ、平均値や相関係数が同じだからと言って必ずしも2つのデータが同じ傾向にあるとは言えません。
- データ数が少ない場合
- 国語と算数に加えて他の教科や性別など変数が増えた場合
には基本統計量をそろえるだけでは限界があります。
こういった場合には、2つのデータに傾向の差がでてしまうことを前提条件としてデータを分割する交差検証という手法があります。
2-3. 交差検証法によってデータの分割を最適化
交差検証とは、1つのデータを訓練データと検証データに分けるときに複数の分け方をして平均をとるという方法です。データの分け方を複数作ることでリスクを分散し、訓練データと検証データの傾向の違いにより生じる過学習を最小化します。今回は交差検証の中でも最もよく使われるK-交差検証法についてご紹介します。
交差検証で最もよく使われるK-交差検証
K-交差検証ではまずK個にデータを分割します。A~Kまであるうち、最初にAを検証データにしてB~Kのデータから予測モデルを作成。次にBを検証データにしてAとC~Kのデータから予測モデルを作成。という流れで順番にK回検証していきます。
【K=10の時のイメージ】
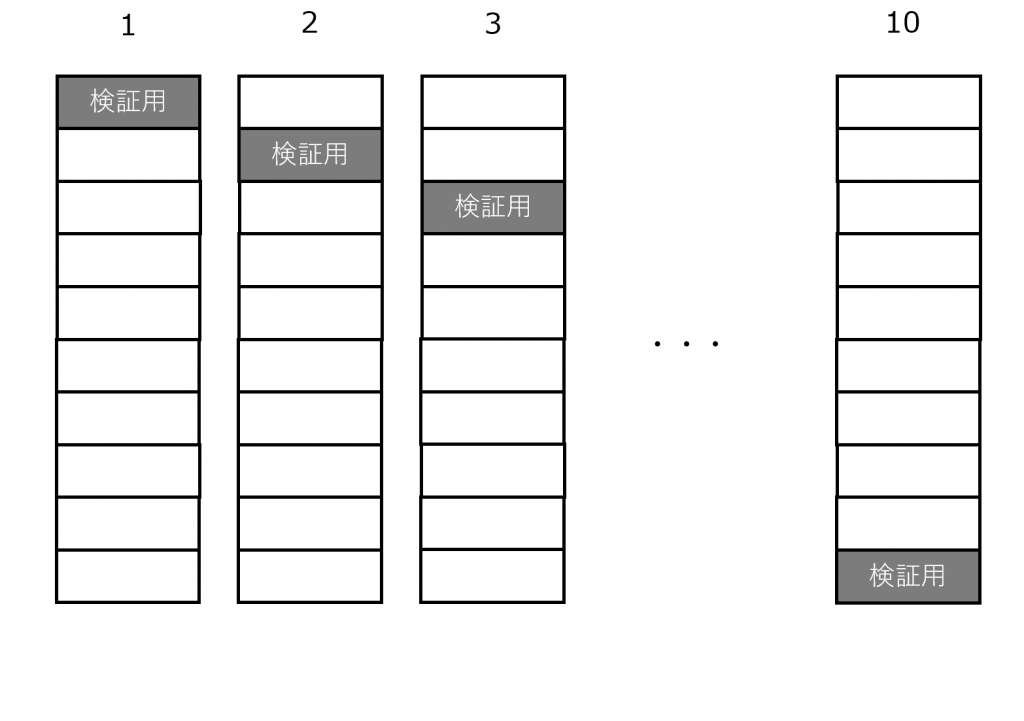
こうしてできたK個のモデルを平均してモデルを決定します。
K-交差検証の注意点
交差検証はK通りの分割と検証を試す分、コンピューターに計算負荷がかかります。なので10万以上など膨大な量のデータがあると計算に時間がかかることがあります。あまりにデータ量が多い時にはホールドアウト法に切り替えるなど柔軟に対応しましょう。
ホールドアウト法との使い分け
データの量が10万以下であれば交差検証で万全な分析を行いましょう。あまりに膨大なデータを扱う場合やコンピューターが低スペックの場合はホールドアウト法を選ぶことで計算に時間を取られずに済みます。
2-4. 学習曲線による過学習の判別
ホールドアウト法でも交差検証法でも、学習曲線の図を作成します。学習曲線とは下の図のように作ったモデルの訓練データへの精度と検証データへの精度を表すものです。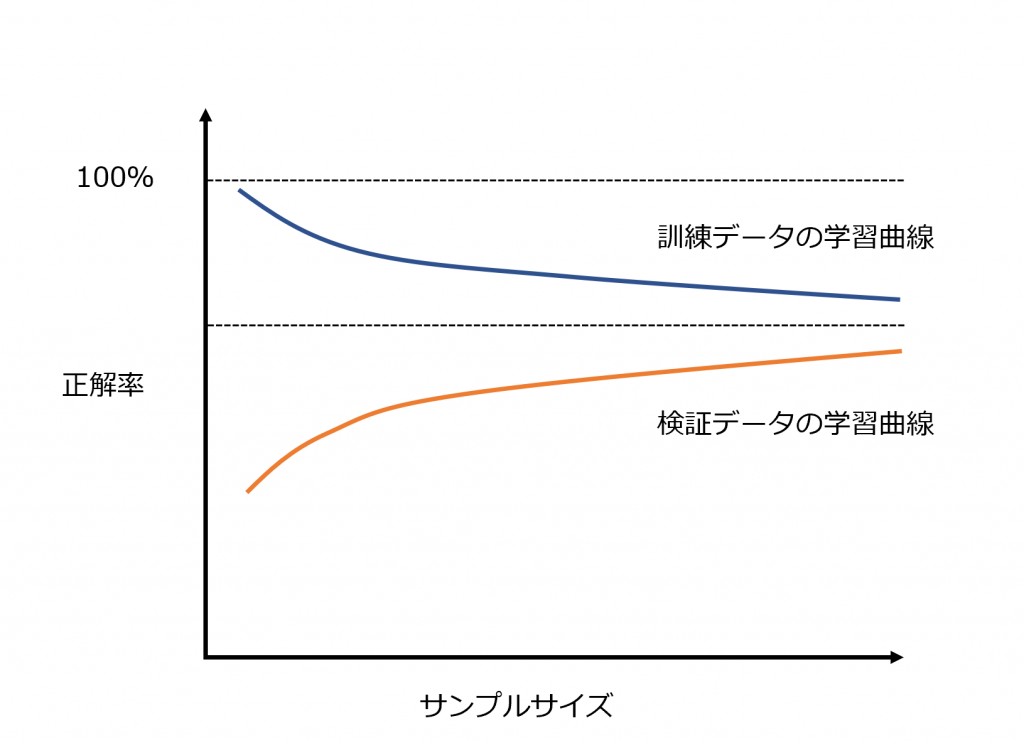
学習曲線の見方
学習曲線を見るときには訓練データの曲線と検証データの曲線の間にあるギャップに注目します。このギャップが大きければ予測モデルとしては使えない、ということです。また、訓練データに高い精度を発揮できているのにギャップが大きい場合、過学習の状態にあるといえます。
学習曲線を見ることで2つのことがわかります
- サンプル数は十分に足りているか
- モデルは過学習になっていないか
サンプル数は十分に足りているか
サンプル数が少ないほど1つ1つのサンプルにフィットしすぎてデータ全体の傾向がつかみにくくなるので、2つの学習曲線のギャップが大きくなります。この図で〇に囲まれている部分ではサンプル数が明らかに足りていません。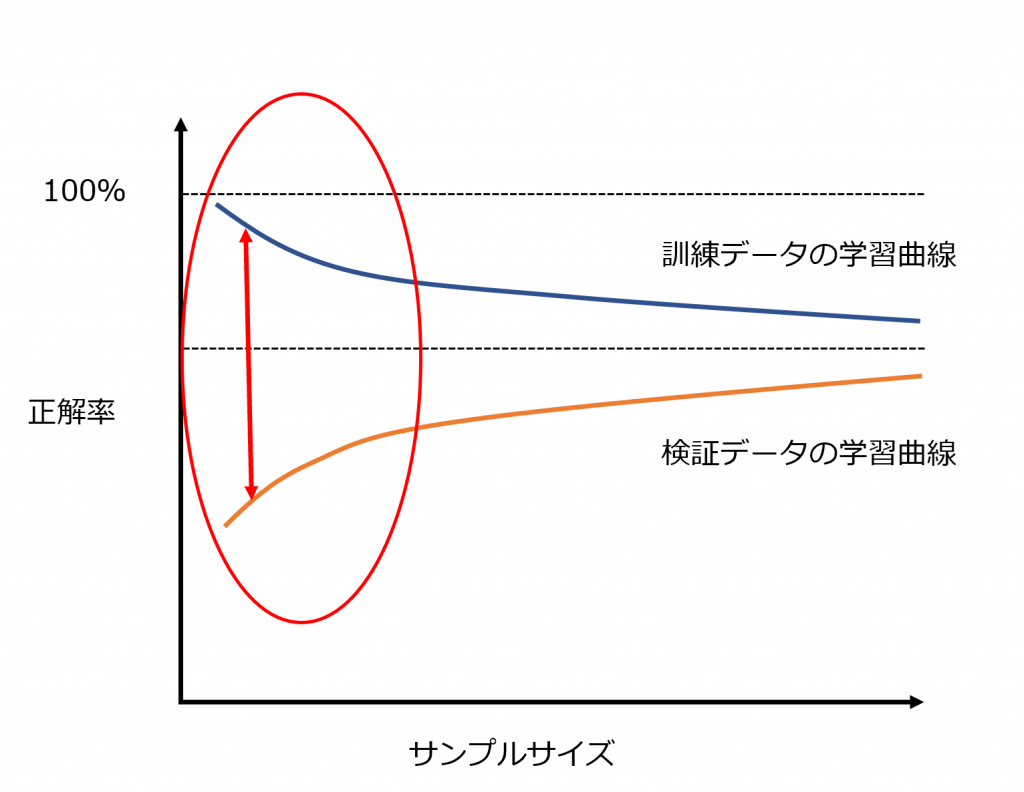
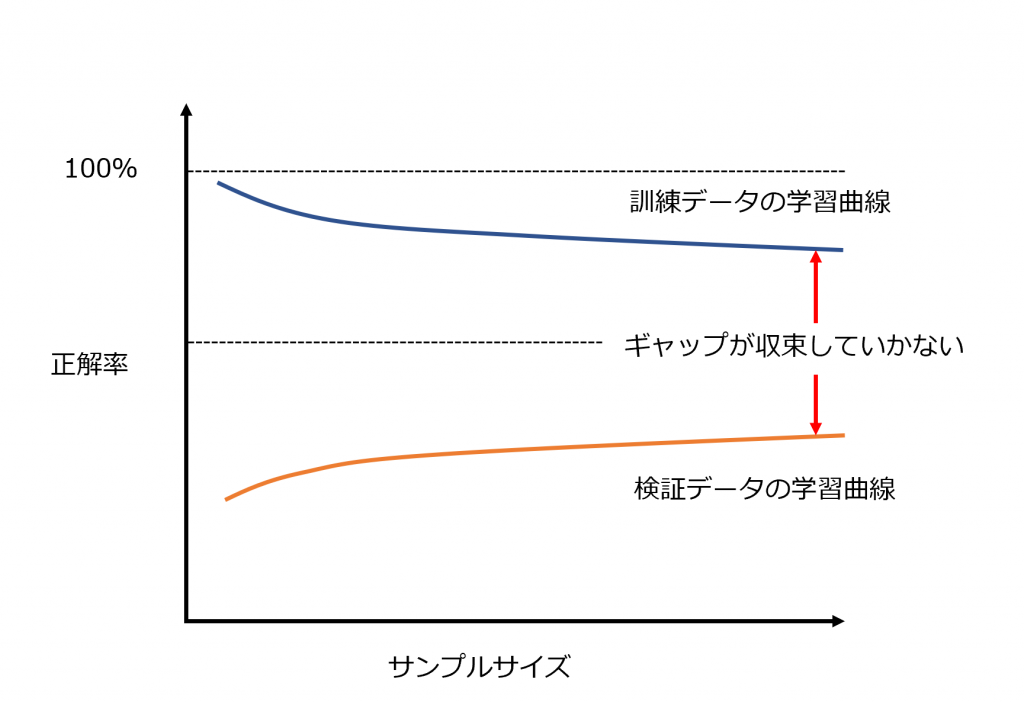
モデルは過学習になっていないか
サンプル数が問題の場合は単純にサンプル数を増やせばいいのですが、サンプル数が足りているはずなのにギャップが収束していかない場合、根本的なモデルから見直す必要があります。
第3章 過学習を解決する方法
過学習の対策は基本的にモデルの自由度に制限をかけるものです。第1章でご紹介したとおり、過学習とは全体の傾向が読み取れずに1つ1つのデータにフィットしてしまうことです。そのため、1つ1つのデータにフィットしすぎないように予測モデルに制約をかけるという発想で過学習を解決していきます。
3-1. 過学習を解決する代表的な手法
過学習はモデルを作成する分析手法によって対処法が変わってきます。分析手法ごとに代表的な過学習解決方法をまとめたものを一覧表にしました。
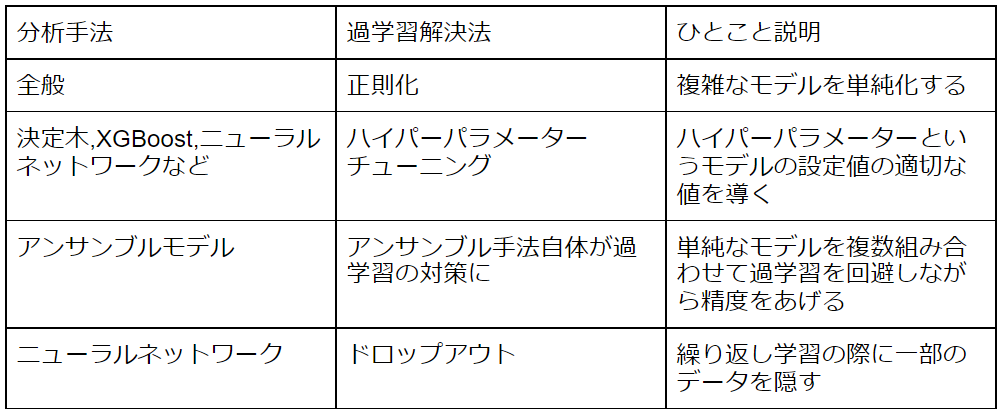
それぞれの対策法について簡単にご説明します。
3-2. 過学習が発生したらまずは正則化
正則化とは、複雑になったモデルをシンプルにすることで過学習を解決するという手法です。どんな分析手法においても過学習対策に使える最も汎用性の高い手法なので今回は重点的に解説していきます。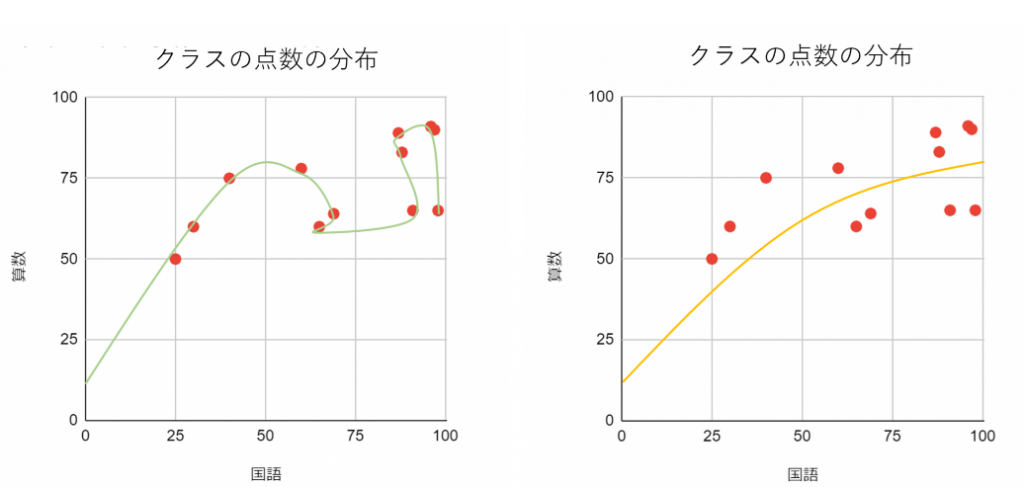
正則化の前提知識
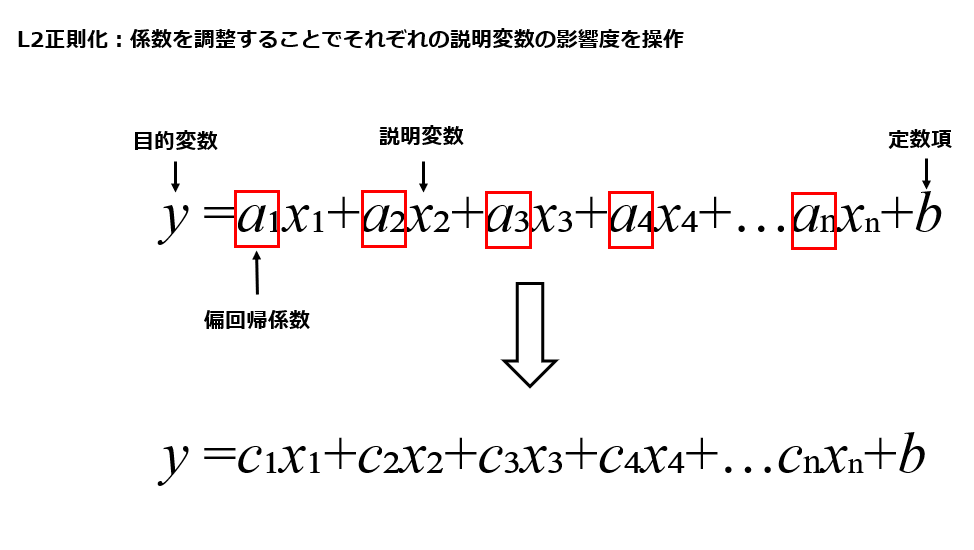
正則化で解決されるモデルの複雑さとは、1章で示したようなぐにゃぐにゃとしたモデルの状態を指します。重回帰分析のような「複数の説明変数を使って目的変数の予測を行う数値予測型の予測モデル」においては説明変数の数と説明変数それぞれの係数がモデルの複雑さを決定します。(重回帰分析について詳しく知りたい場合はこちらの記事をご参照ください)
特に以下の3つの場合にモデルは複雑になります。
- 説明変数の数が多すぎる
- 必要のない説明変数がある
- 偏回帰係数の値における大小の差が著しい
それぞれ重回帰分析を数式で表すと下の図のように表示される値です。目的変数が実際に予測したいカテゴリの値、説明変数が予測の基となる値、偏回帰係数は予測のためにそれぞれの説明変数に掛け合わせる値です。
【重回帰分析の数式】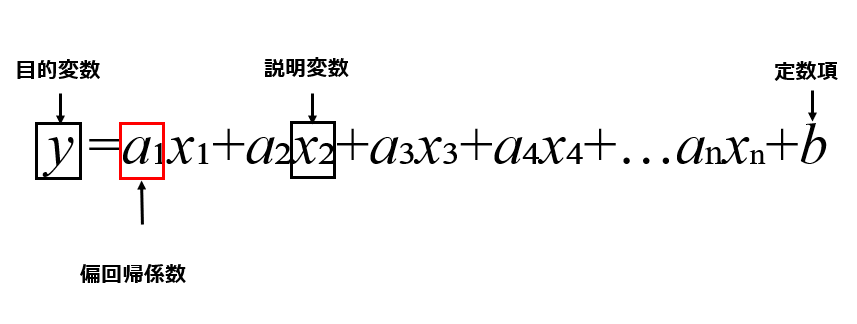
正則化による過学習の解決
複雑すぎるモデルは精度は高くても過学習に陥っていて予測としては使えない、といった欠点があります。一方でシンプルすぎるモデルはそもそも訓練データへの精度に問題がある場合があります。正則化によって、2つのモデルの中間にあるバランスのとれたモデルの作成を目指しましょう。正則化には以下の2つの手法があります。
- L1正則化:必要のない説明変数の影響を0にする
- L2正則化:モデルを複雑化させている説明変数の影響を小さくする
正則化は数式を使って説明されることが多いですが、今回は初心者向けということで数学的な知識がない人でも理解できるよう数式はなしで解説していきます。
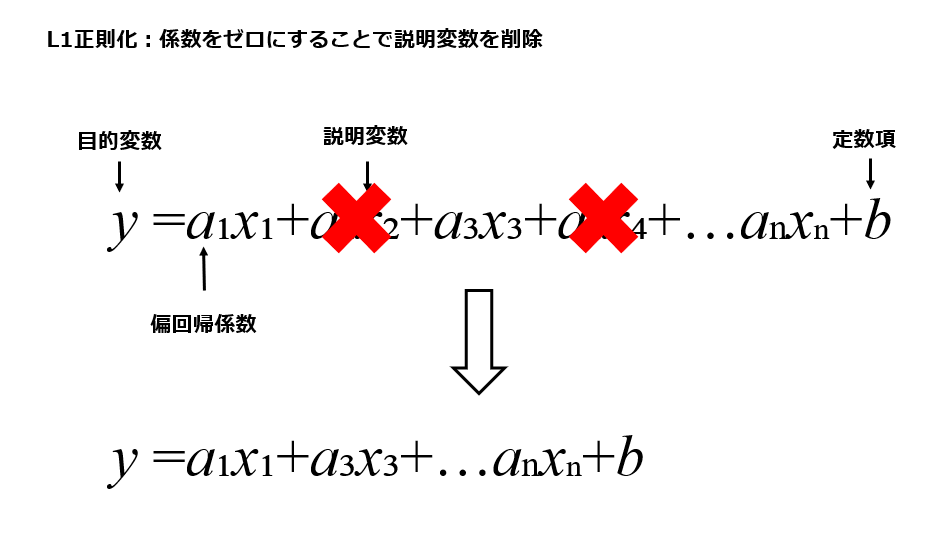
必要な説明変数をはっきりさせる正則化(L1正則化)
予測モデルを構成する複数の説明変数の中から必要のない説明変数を無効化する正則化をL1正則化といいます。この手法は特に説明変数が多すぎるせいでモデルが複雑になり過学習が発生する際に有効です。
予測モデルを滑らかにする正則化(L2正則化)
複雑になった予測モデルを平滑化してシンプルにする正則化をL2正則化といいます。L2正則化は説明変数自体の数を減らさずに偏回帰係数を調整することでモデルを改善する方法です。この手法は特に特定の偏回帰係数が大きすぎてモデルに偏りが出ているときにオススメです。
L1正則化とL2正則化の使い分け
この2つの正則化はデータ数が多いか少ないか、説明変数の数が多いか少ないかで使い分けます。
- データ数も説明変数の数も多い場合
- L1正則化によって説明変数の数自体を思い切って減らす
- データ数が少なく、説明変数の数も多くない場合
- L2正則化によって偏回帰係数を最適化する
どちらを使うべきか迷った際にはモデルにL1正則化とL2正則化を両方試してみて、検証曲線のギャップがよりよく収束していく方を採用するのがオススメです。
この正則化について、第4章で実際に使用して過学習を解決します。
3-3. モデルの設定を最適化するハイパーパラメーターチューニング
ハイパーパラメーターチューニングはそれぞれの分析手法において予測モデルの自由度を決定する設定を最適化することです。例えば決定木分析においては木が深ければ深いほどモデルが複雑化してしまうので木の深さというハイパーパラメーターを適切な値に設定することで過学習を防ぐことができます。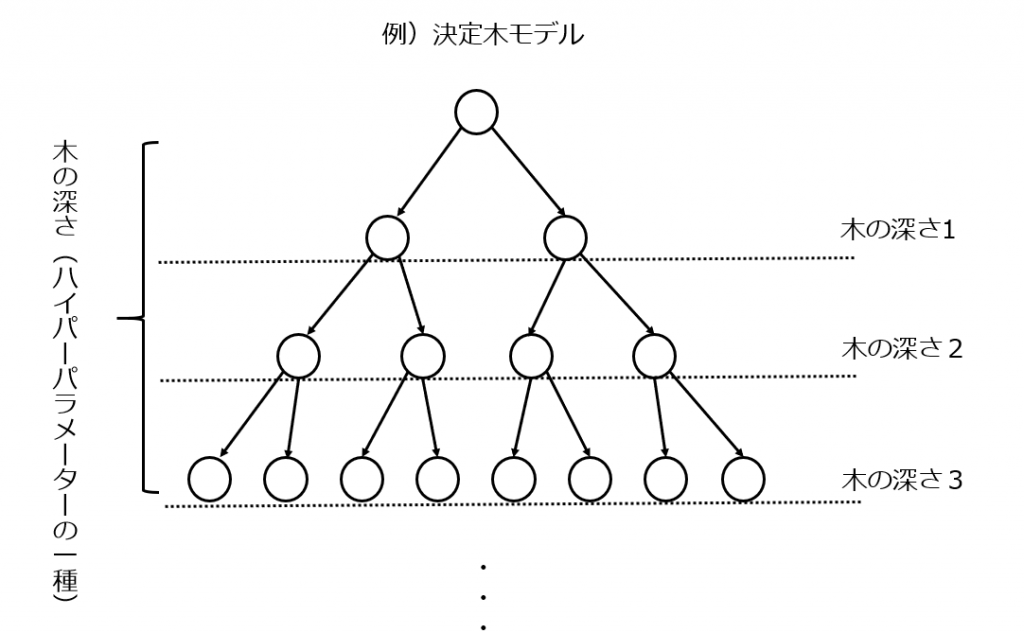
3-4. 複数にデータを分割してモデルを構築するアンサンブルモデル
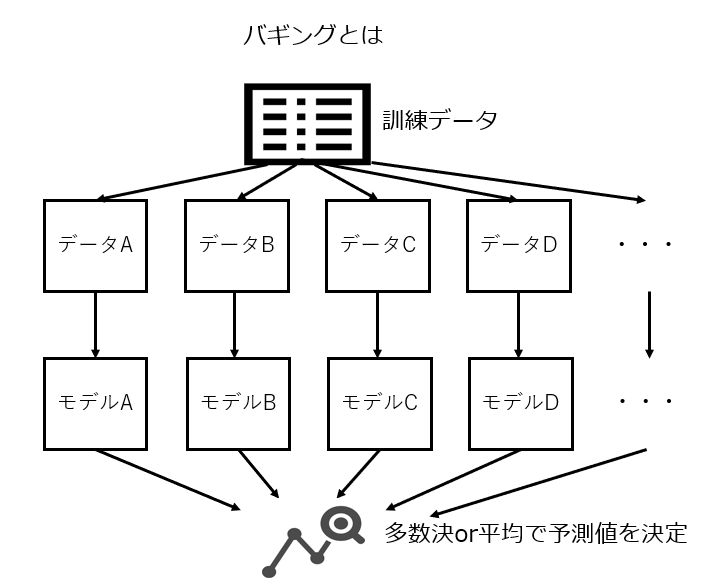
アンサンブルモデルは重回帰分析やロジスティック回帰分析、決定木分析といった基本的な学習器を組み合わせることで過学習を避けながらモデルの精度を上げていくものです。主に3つの手法で分析精度を向上させています。
- バギング:データを複数に分割してそれぞれを異なる手法で予測、モデルの平均や多数決をとる手法。代表的なものはランダムフォレスト。
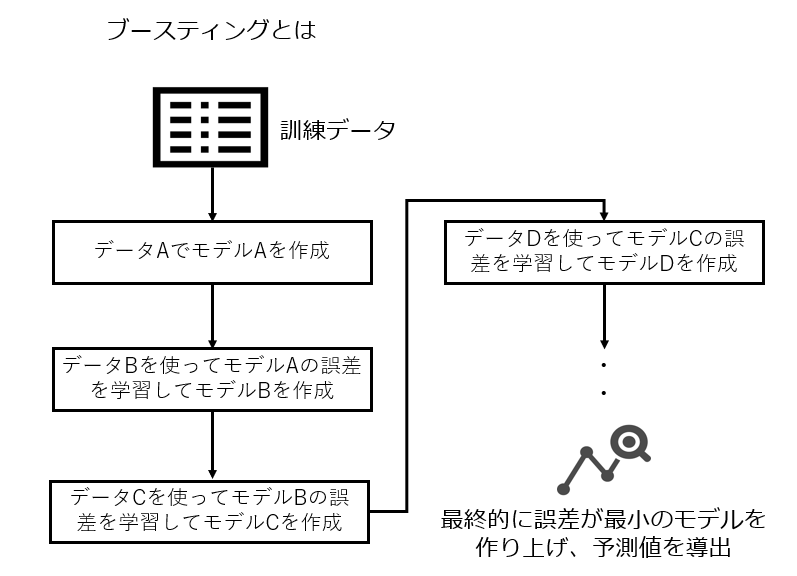
- ブースティング:複数のデータに順番をつけ、前の学習結果を次の学習に影響させる手法。代表的なものはLightGBMやXGboost。
- スタッキング:複数のモデルを積み上げていく手法。1段目のモデルの予測値を2段目のモデルが予測に使う。
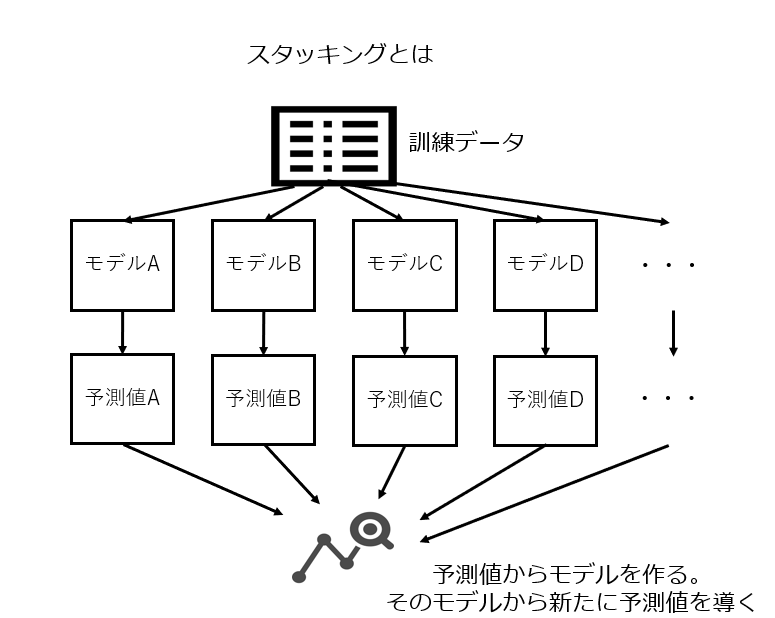
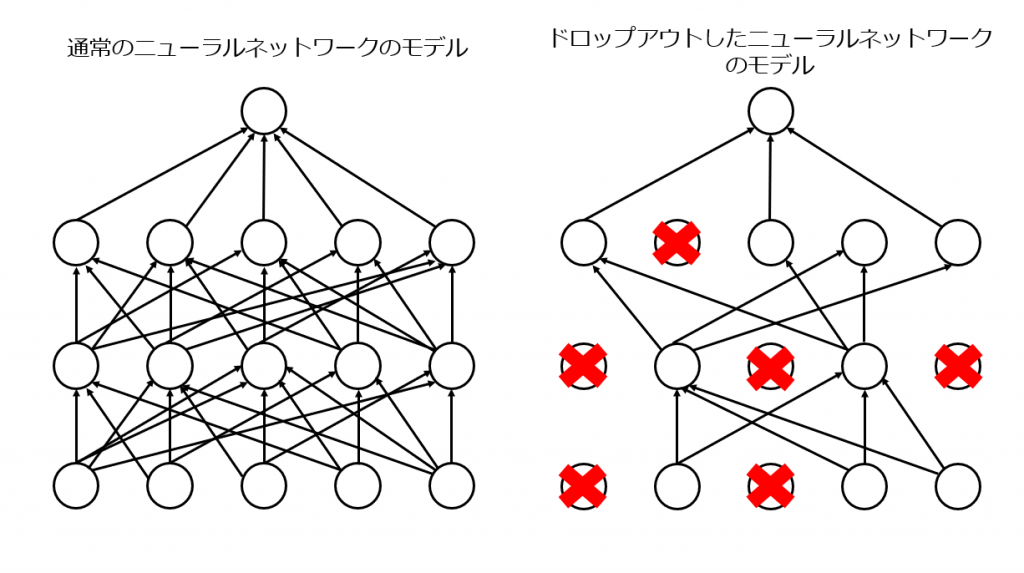
3-5. データの一部を隠すことで過学習を避けるドロップアウト
ドロップアウトは特にニューラルネットワークで用いられます。ニューラルネットワークが行う繰り返し学習によるモデルの複雑化を解消し、シンプルにする手法です。データのすべてを学習するのではなくデータから一部を抽出して学習させます。
第4章 過学習の発見・解決事例
3ステップで過学習の発生から発見、解決までの流れを具体例を用いながらイメージしていただければと思います。重回帰分析を例に第2章でご説明した交差検証と第3章でご紹介した正則化を用いて過学習を解決していきます。
4-1. ステップ①モデルを作成
過学習になった予測モデルを正則化で解決する具体例を示していきます。
正則化によって過学習を解決できる予測モデルの具体例
よく使われる分析手法の重回帰分析を例にご説明していきます。先ほども述べましたが、重回帰分析とは複数の説明変数から1つの目的変数を導く分析手法です。
不動産の適正価格の予測を例に考えてみましょう。ある分譲マンションの1室を査定できるモデルを作成しようとしています。分譲マンション物件のデータを集め、目的変数である価格をいくつかの説明変数から予測するモデルを構築しています。

【説明変数】
- 駅から歩いてかかる時間(分)
- エリアのグレード
- 坪数
- 坪単価
- 築年数
- 部屋のグレード
- トイレはいくつあるか
- 外観のよさ
- 駐車場の有無
などなど。これらの説明変数を使って訓練データに90%適合したモデルができました。
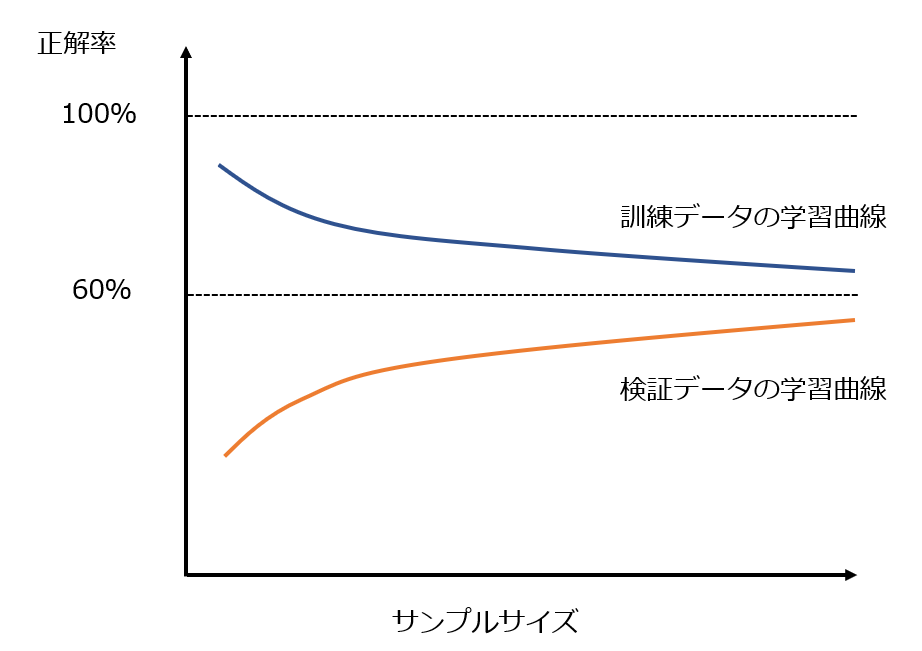
4-2. ステップ②交差検証と学習曲線
しかし、交差検証を行い学習曲線を見てみると…まさに過学習といった結果になってしまいました。L1正則化によって必要のない説明変数を削除し、L2正則化によって外れ値の影響を最小化することでこの過学習を解決していきましょう。

4-3. ステップ③正則化で過学習を解決
L1正則化による解決
L1正則化をしてみたところ、「坪単価」「坪数」以外すべての説明変数の係数が0にされてしまいました。学習曲線を導出してみると確かに過学習傾向は解消されましたが、そもそもの精度自体も下がってしまっています。
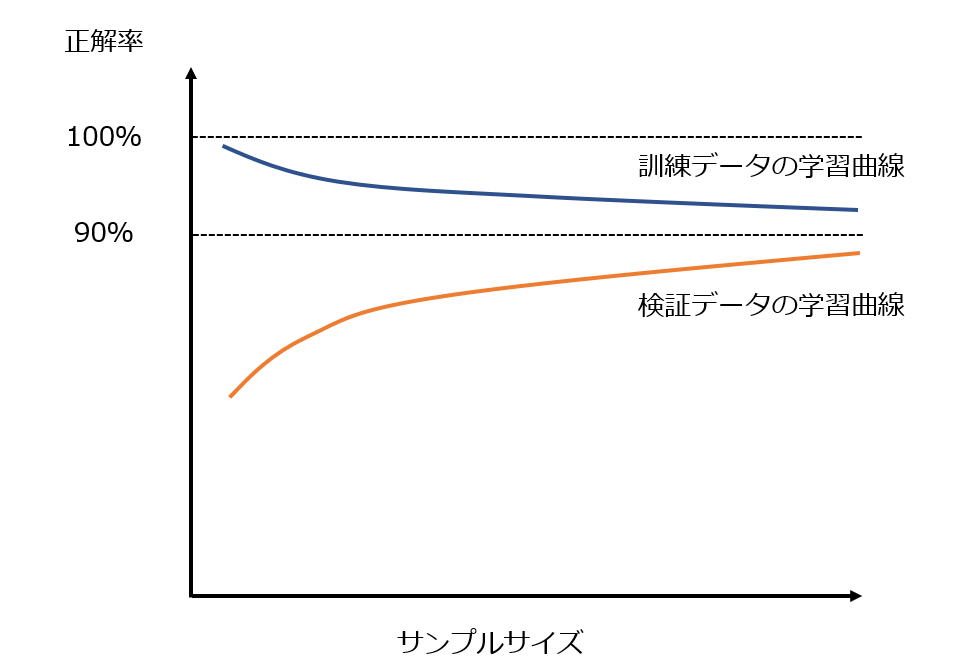
L2正則化による解決
L2正則化をしてみたところ、極端に値が小さくなった説明変数が3つありました。「部屋のグレード」、「トイレはいくつあるか」、「外観のよさ」がその3つでした。
実際にデータの出どころから調べてみたところ、以下の2つがわかりました。
- 「部屋のグレード」や「外観のよさ」は基準がなく、担当者の主観で決まっている
- 「トイレの数」は2個以上あるところがほとんどないので予測に対してあまり有効なデータでない
上記3つの説明変数を取り除いたうえで再度重回帰分析を行い、L2正則化によって偏回帰係数を調整してみた結果、もともとの90%という精度を検証データにおいても達成することができました。これで過学習が解決できましたね!
第5章 まとめ
今回はデータ分析初心者の方向けに、過学習を乗り越えるための基本的な対策方法について詳しくご紹介しました。
過学習は何か対策をすれば防げるものではなく都度都度検証しなくてはいけないめんどくさい問題ですが、過学習のことを理解しているだけでもデータ分析のレベルが1段階も2段階も変わってくるので、ぜひ分析をしながら繰り返し対策をして慣れていってください。
今回の記事でご紹介した基本的な過学習の対策方法をマスターして、より精度の高いモデルの作成にチャレンジしていきましょう。
今すぐにデータ分析をしてみたい方はぜひKaggleというコンペティションに参加してみてください。無料で実際にビジネスや研究で使われているデータが公開されています。リンクはこちらです。
データの管理・活用でお困りの場合はデータビズラボへお問い合わせください。
状況やニーズに合わせた様々なサポートをご提供いたします。





コメント