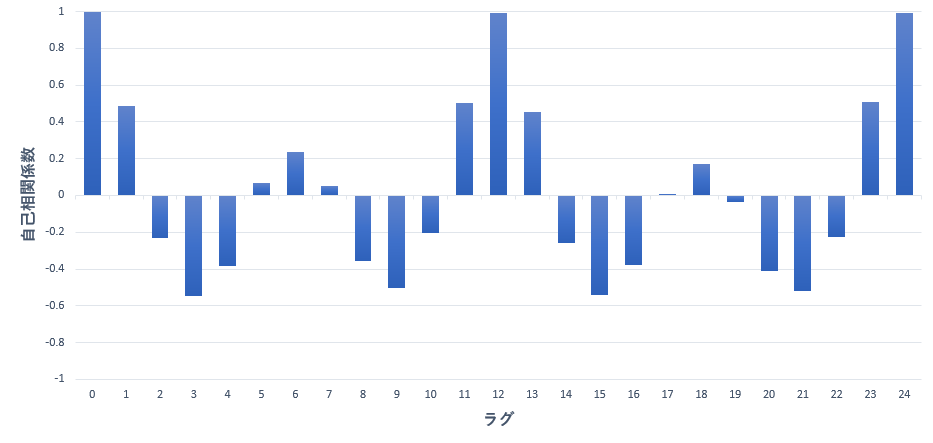
コレログラムとは、数あるビジュアライゼーション表現の中でも、データの周期性を掴むことができるグラフ形式です。
本記事は、
- コレログラムについて知りたい
- 統計学の知識を深めたい
- コレログラムについてのサイトをいくつか読んだけれど、どれも解説が分かりづらかった
このような方におすすめです。
統計検定2級でも出題されるコレログラムの概要から活用シーンまで、図解を用いて解説します。
目次
コレログラムとはラグと自己相関で表されたグラフ
コレログラムとは、元データxから時間をずらしたデータyとの相関係数を表すグラフであり、横軸にラグ、縦軸に自己相関をとります。
自己相関:ずらしたデータと元データの相関関係を表す指標
(ラグと自己相関については後段で詳しく解説しています。)
コレログラムを理解するにあたり、まずはその元になるデータをみていきましょう。
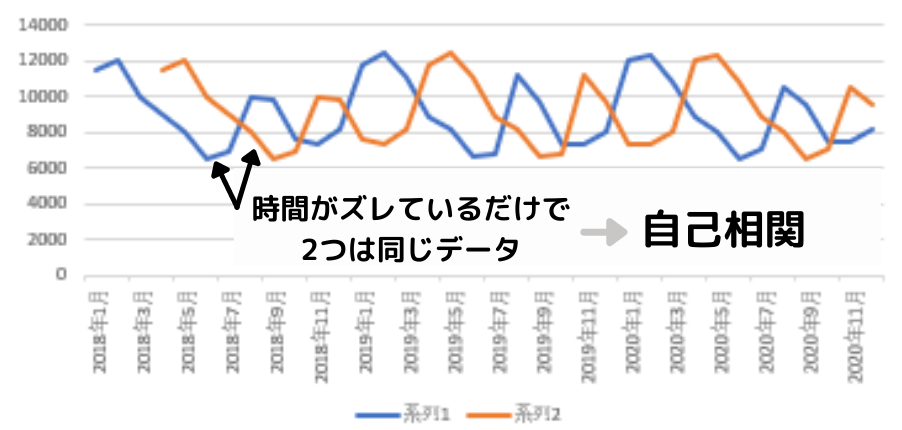
下図は3年間の電気代使用料の変動を表す線グラフになります。
この表をコレログラムで表すと下図のようになります。
▼2018年1月~2020年12月までの電気代使用料のコレログラム
ちなみにコレログラムは以下のような線グラフで表されることもあります。
コレログラムの完成系のイメージを掴めたところで、次にラグと自己相関について詳しく解説していきます。
ラグとは、元データからずらす時間の度合いを表す指標である
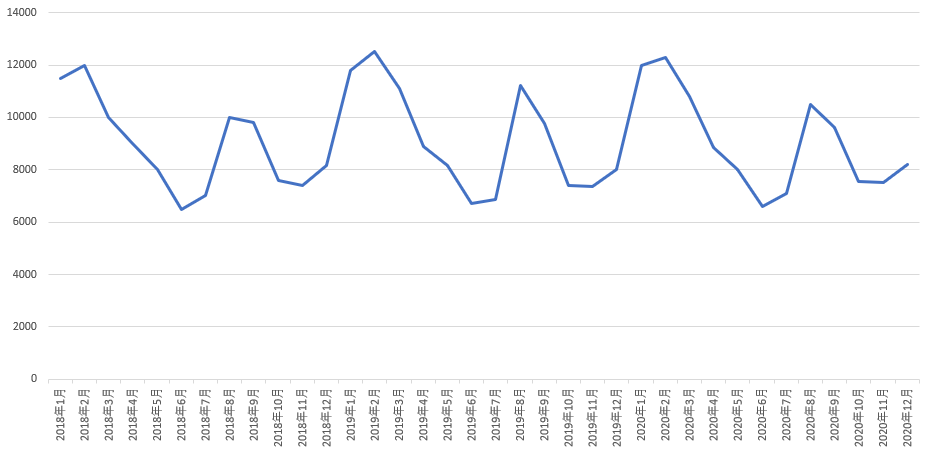
ラグとは、前述の通り元データxからどれほど時間をずらしているかを表す指標のことです。例えば、下記の表は元データxとラグを与えたデータyの値を並べた表になります。ラグが1の時は、yは元データから時間軸が1カ月遅れていることがわかります。同様にラグが3の時は、yは元データから時間軸が3か月遅れていることがわかります。
この表から、ラグ1、ラグ3、ラグ6、ラグ12地点のデータをグラフにしてみると以下のようになります。
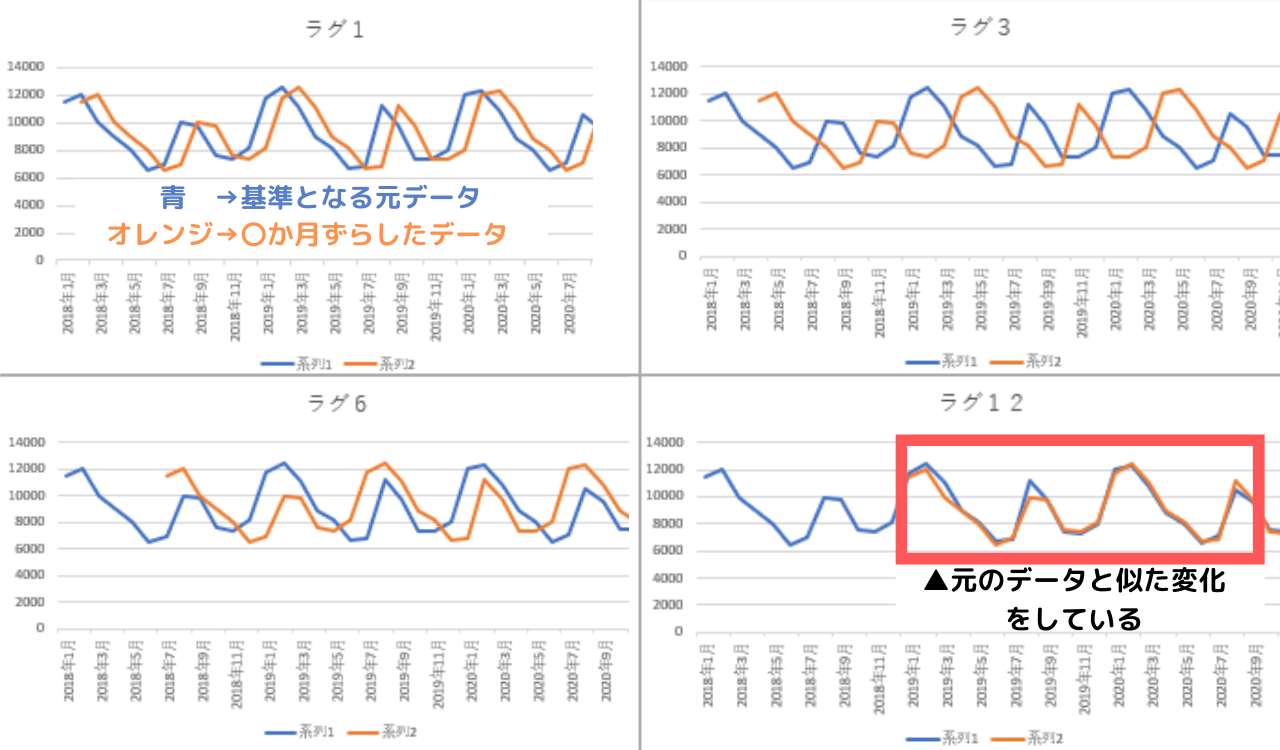
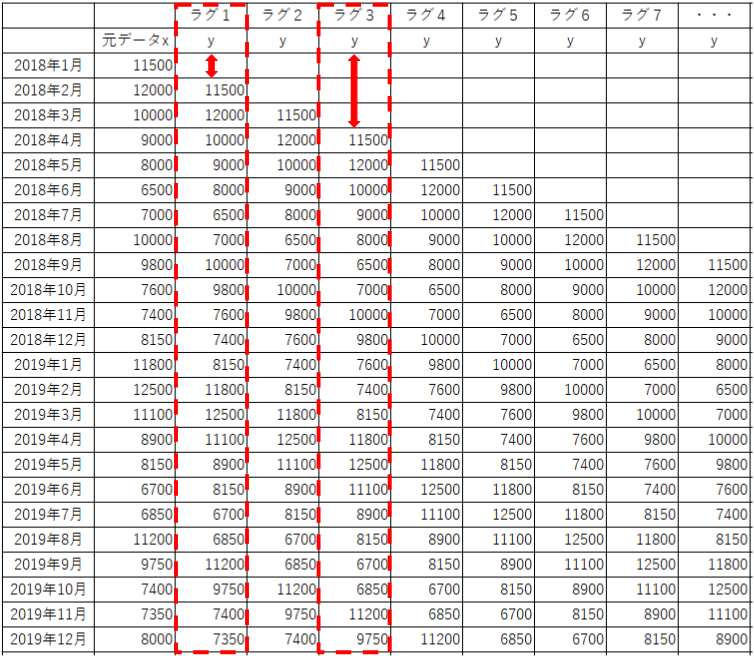
今回、ラグ12のデータが最も元データと似た変化をしていることから、この2つの相関関係は強いことがわかります。
実際にコレログラムで確認してみると、ラグ12地点の相関係数の値は他の地点と比較して大きいことが見てとれます。
自己相関とは、ずらしたデータと元データの相関関係を表す指標である
自己相関とは、ずらしたデータと元データの相関関係を表す指標のことです。時間をずらしたデータと元データはあくまでも同一のデータであるため、2つのデータ同士の相関関係のことを自己相関といいます。
▼相関関係について詳しく知りたい方はこちら
『相関係数とは?意味や求め方、エクセルでの計算方法をわかりやすく解説』
『相関分析とは?分析初心者でもわかる解説とExcelでのやり方を紹介』
以下は先ほどの3年間の電気代使用料を自己相関グラフにより表したものになります。
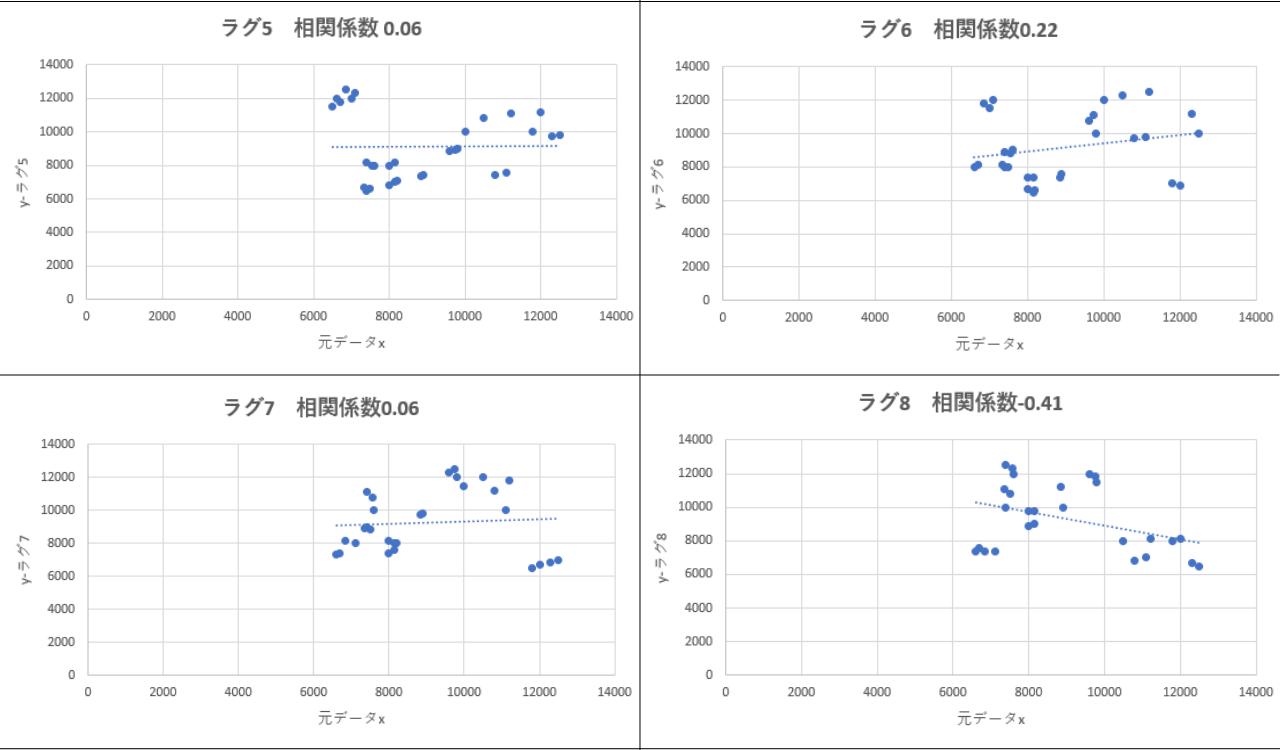
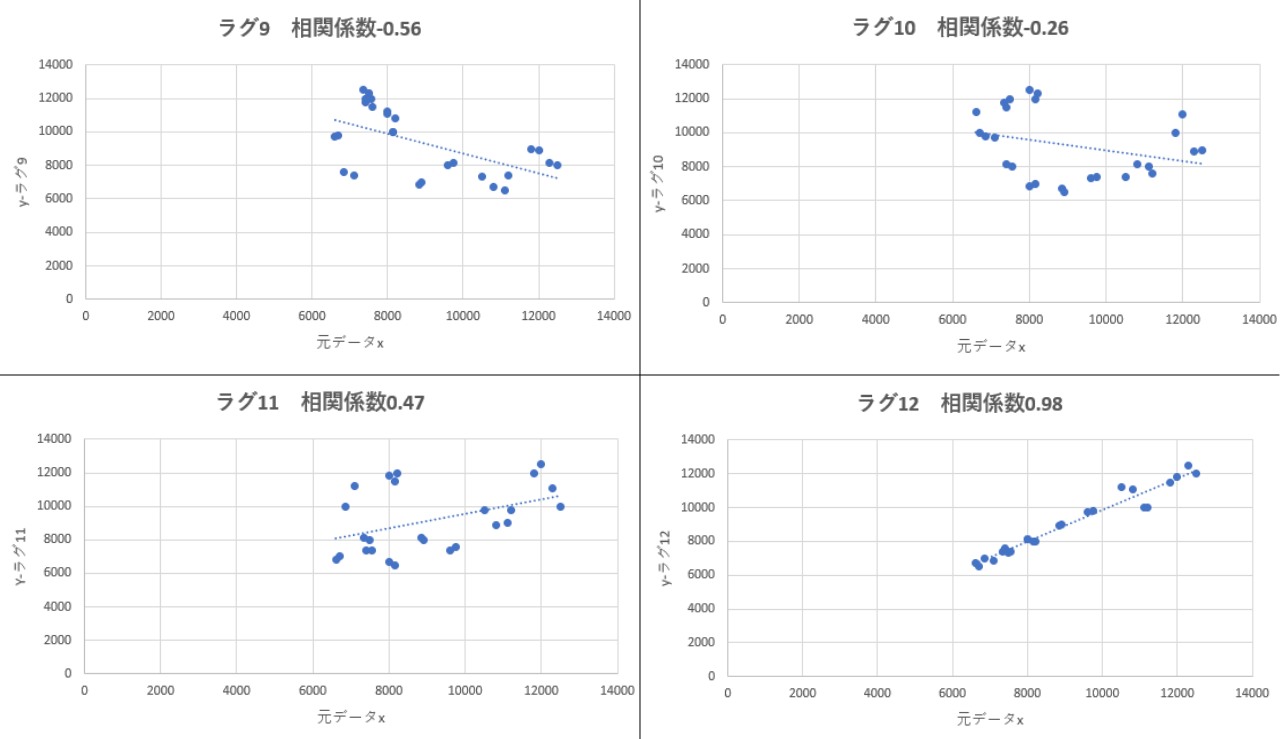
各グラフを見ると、コレログラムがラグを横軸に、元データxと時間をずらしたデータyの相関係数を縦軸に表したものであるということのイメージが付くと思います。
一方で、なぜこのように時間をずらしたデータをグラフ化するのでしょうか。次章では、コレログラムを使用するメリットや活用シーンについて解説していきます。
コレログラムはデータの周期性を把握することができる
コレログラムには、データの周期性を掴むことができるというメリットがあります。
下図の電気代使用料の変動を表すコレログラムをみてみると、ラグが「12」、「24」近辺で正の相関が強くなり、逆に「3」、「9」、「15」、「21」近辺では負の相関があることがわかります。よって今回のコレログラムは12カ月の周期をもつと言えます。このように周期性を掴めるコレログラムは実際に様々な場面で活用されます。実際にどんな場面でコレログラムは使用されるのか次の章で見ていきましょう。
- データに規則性があるか知りたいとき
- 時系列が自己回帰であるか知りたいとき
- 時系列がホワイトノイズであるか知りたいとき
- 時系列が正弦波であるか知りたいとき
- 時系列が自己回帰であるか知りたいとき
統計データ可視化を成功させる95のチェックリストをダウンロードする
さいごに
今回は、統計検定でも出題されるコレログラムについて、その概要から活用シーンまで図解を用いて解説しました。コレログラムは一目では理解し難いグラフですが、一度理解してしまえば忘れることも中々ありません。本記事を読むことで、皆様のコレログラムに関する知識が確かなものになれば幸いです。
以下に統計検定3級に関する記事を載せておきます。統計検定受験を検討されている方も、そうでない方もぜひご一読ください。



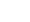



コメント