確率過程とは？-具体例で解説-

確率過程は、統計検定準一級合格を目指す方、実践的な時系列分析を行う方が押さえておくべき重要な分野の一つです。確率過程は、時系列分析に関する各種統計モデルを理解する上での前提知識となるため、主要な式や定義を説明できるレベルの詳細な理解が求められます。

しかし、確率過程の定義や概念について『統計学実践ワークブック』をはじめとした教材では数式ベースの抽象的な説明が多く、直観的な理解が不足しがちです。

本記事では、統計検定準一級、時系列分析を学習している方を対象に、確率過程の定義や概念を具体例を用いて丁寧に紐解いていきます。確率過程が何か直観的に理解できるよう、具体例を用いた解説を重点的に行っています。

本記事は読者が統計検定二級程度の知識を有していることを前提としています。また、本記事は数学的に厳密な解説ではなく、具体例ベースで直観的な理解を助けるような解説をしています。正確な数学的定義・数式の導出については、適宜参考書や各大学の講義資料などをご参照いただければと思います。

1.確率過程とは

確率過程は、正式には以下のように定義されます。

少し難しい表現に感じられますが、t を時間を表す数と捉えると、「時間を表す数t（タイミング）を定めたとき、t に応じて確率的に発生する値X の集まりを確率過程という」と言い換えることができます。

具体例を見てみましょう。

具体例①

スタート地点から0、1、2、…のように番号が順番に各マスに振られているすごろくを考える。スタート地点を0とし、サイコロを転がして出た目の数だけ試行前の地点から進むこととする。例えば、1回目の試行（サイコロの投擲）で6の目が出たときには6のマスに、2回目の試行で2が出たとには8のマスに進む。各試行をti（i=1, 2, 3）とし、各試行終了時点で自身がいるマスの番号をXti（i=1, 2, 3）とする。例えば、1回目の試行で3の目が出たとき、Xt1は3、2回目の試行で4の目が出たとき、Xt2は7（＝3 + 4)となる。

実際にすごろくを行った結果が表1です。

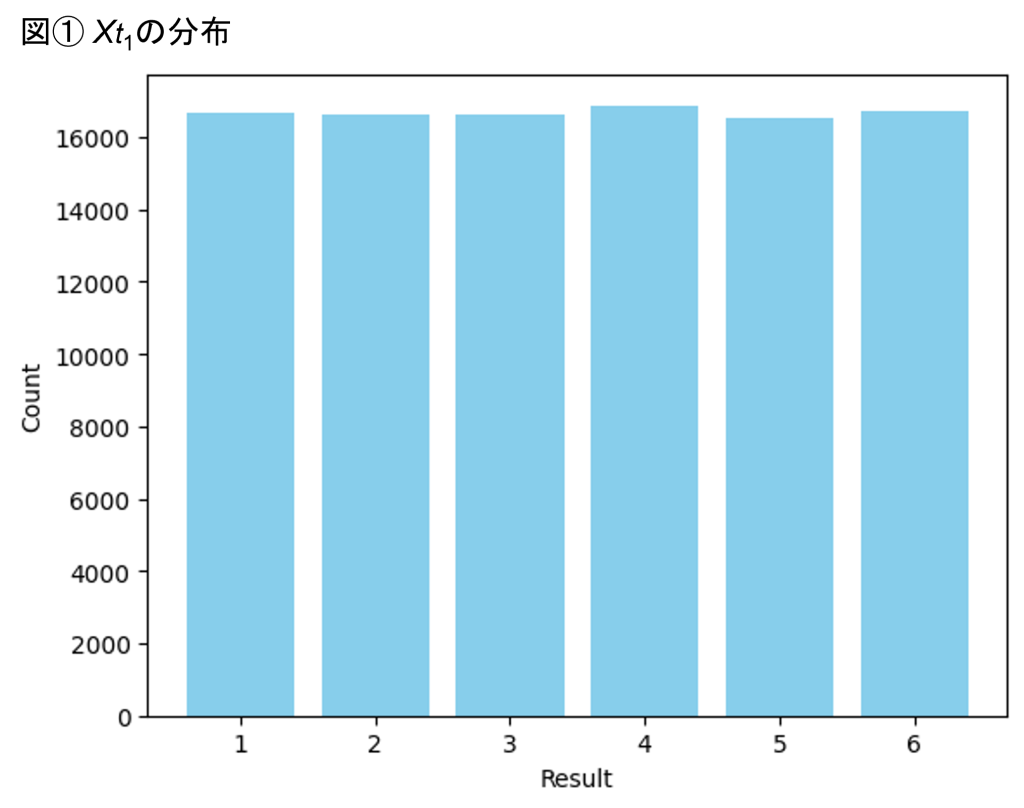
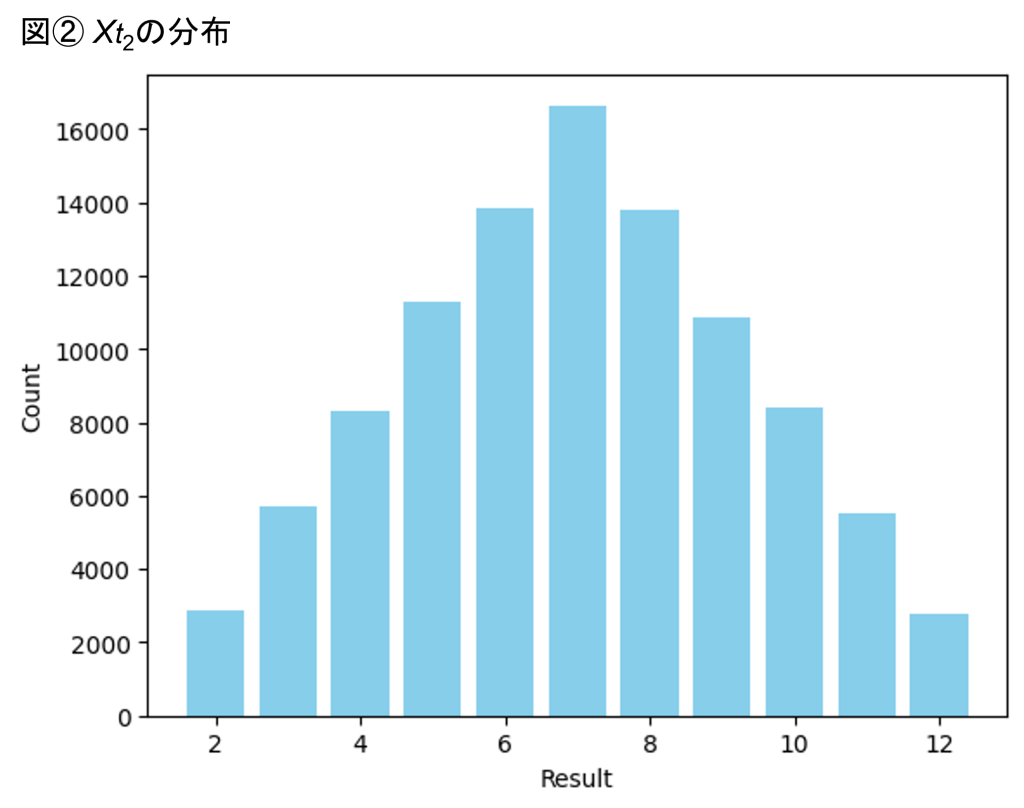
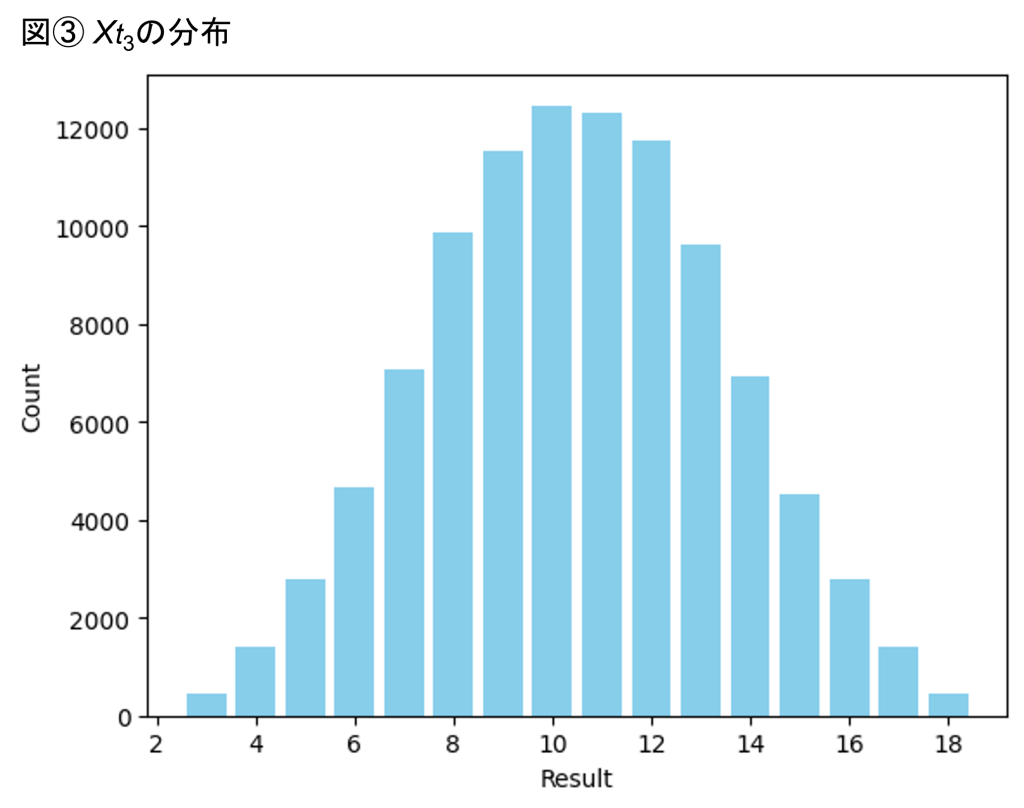
ここで重要な観点は、1回目、2回目、3回目のサイコロの目は確率変数であることです。全てのサイコロの目が等しい確率で出現すると想定すると、Xt1, Xt2, Xt3の分布はそれぞれ図①、図②、図③のようになります。

図①～③はXt1, Xt2, Xt3（サイコロを転がした後のすごろくのマス目の番号）の分布をとったヒストグラムです。100,000回試行を行った結果、それぞれの番号のマス目にいた回数をプロットしています。ここで特に着目すべき点は、図①～③は全く別の分布になっている点です。サイコロを転がした後のすごろくのマス目の番号は、その試行が何回目なのかに応じて、それぞれ別々の確率分布に従っているのです。

具体例①のように、t に応じて発生する確率変数Xt を、tが0以上のあらゆる範囲をとりうる数として一般化した概念が確率過程です。確率変数Xt は、各tごとに別個の確率密度関数または確率質量関数に従います。従って、確率過程が与えられたとき、t ↦Xt の関数を描くことができます。

2.独立増分性と定常増分性

確率過程は幅の広い概念であり、その特性によって様々なモデルが存在します。各時系列分析手法を学習する上で、特に抑えておくべき基本的な確率過程の概念が独立増分性と定常増分性です。それぞれの定義を具体例を見ながら紐解いていきます。

独立増分性

数式ベースの抽象的な表現で理解が難しいと思います。具体例を見てみましょう。

具体例②

コイントスを繰り返し行い、表が出た回数を数える試行を考えます。i回目のコイントスの試行が終わったタイミングをtiとし、ti時点での表が出た回数の合計をXtiとすると、Xは確率過程と捉えることができます。実際の試行結果は表2のようになりました。

この試行結果から2つの区間をとります。

• [i, i-1]=[5, 4]…4回目終了時点と5回目終了時点を比べたときの、表が出た回数の差

Xti – Xt(i-1) = Xt5 – Xt4 （a）= 3 – 2 = 1…4回目終了時点と5回目終了時点を比べたときの、表が出た回数の差

• [i, i-1]=[8, 7]…7回目終了時点と8回目終了時点を比べたときの、表が出た回数の差

Xti – Xt(i-1) = Xt8 – Xt7 （b）= 3 – 3 = 0…7回目終了時点と8回目終了時点を比べたときの、表が出た回数の差

このとき、(a)と(b)は独立の関係になっています。

ある事象Aの発生（あるいはその確率）が別の事象Bの発生確率に影響を及ぼさないとき、AとBは独立であるといいます。例えば具体例③の場合、実際の試行結果はXt5 – Xt4 =1 となっていますが、この値が0であろうと1であろうとXt8 – Xt7が｛0, 1｝のどちらをとるか確率が変化することはありません。

つまり、Xtから重なりのない複数の区間をとったとき、各区間内の増分は独立であり、具体例②は独立増分過程といえるのです。

このように、ある区間における増分が、その区間と重なりのない別の区間における増分に影響することがないような確率過程を独立増分過程といいます。

定常増分性

こちらも直観的に理解するのが難しいと思います。具体例を見てみましょう。

具体例③

蛇口を開けて、お風呂にお湯をためる場面を想像してください。時間をt、浴槽に溜まったお湯の量をXtとすると、これは確率過程として考えることができます。このとき、蛇口をひねってお湯が出る量を意図的に増やしたり、減らしたりすることがなかった場合、一定の時間当たりに浴槽に溜まるお湯の量の分布は一定である（※浴槽に溜まるお湯の量は一定ではなく、その分布が一定である）と考えられます。これがまさに定常増分過程です。

数式に当てはめて考えてみます。

蛇口をひねり終わった瞬間をt0 = 0とし、10秒後をt = 10とします。さらにその後の5秒間をh = 5とすると、t + h = 15となり、t0から15秒後ということになります。このとき、Xt+h – Xtは蛇口をひねり終わった瞬間から10秒後と15秒後の間に浴槽に溜まったお湯の量となり、Xh –X0は蛇口をひねり終わった瞬間からの5秒間に浴槽に溜まったお湯の量となります。この状況をグラフにすると、図④のようになります。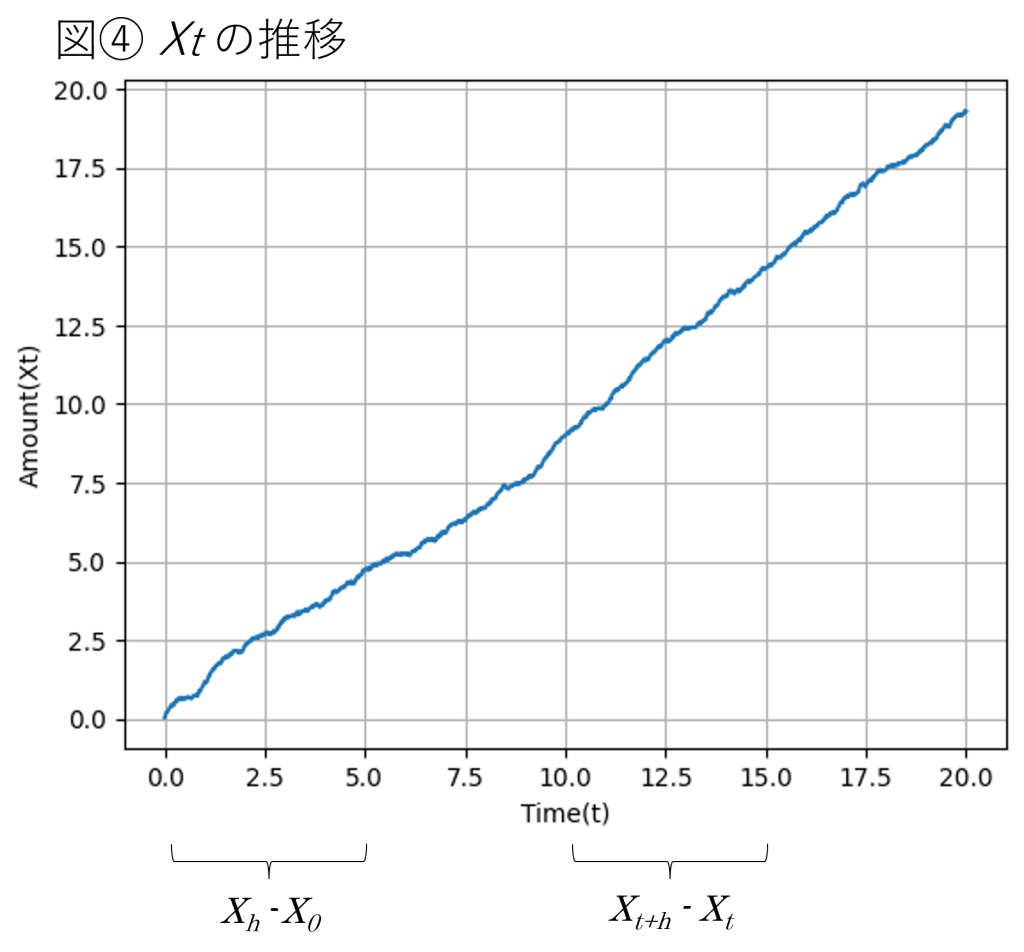

現実世界において蛇口をひねって出てくるお湯の量は常に一定ではないので、必ずしもXt+h – Xt = Xh  – X0となるわけではありません。ただし蛇口をひねって出てくるお湯の量の分布は常に一定であり、従って同じ時間（5秒間）に浴槽にたまるお湯の量を意味するXt+h – Xt とXh  – X0の分布は同一であると考えられるのです。よって具体例③は定常増分過程ということができます。

このように、時間の長さが同一であるどの区間においても、区間内の増分の分布が一定の確率過程を定常増分過程といいます。

また、独立増分過程、定常増分過程両方を満たす確率過程Xを独立定常増分過程といいます。確率過程の基礎として、ここまでで説明してきた内容が理解できていれば、ブラウン運動、ランダムウォーク、ポアソン過程などの応用的な概念についても、理解がしやすいと思います。

3.まとめ

本記事では確率過程の概念及び、基礎的な確率過程である独立増分過程・定常増分過程について解説しました。特に重要なポイントは以下3点です。

具体例を踏まえた上で、以上3点が理解できていれば、確率過程の基礎は抑えられていると言えるでしょう。本記事での解説をベースにブラウン運動、ランダムウォーク、ポアソン過程などより発展的な分野の学習に進むと理解が進むと思います。