
マンデルブロ集合は単純な関数の繰り返しから導かれる魅力的なフラクタルです。その反復の下でどのように振る舞うかを可視化・視覚化したものとして見ることができます。
マンデルブロ集合は、1980年に米国IBMのトーマス・J・ワトソン研究センターでブノワ・マンデルブロによって可視化されました。
データ可視化そのものについて知りたい方は、こちらの記事からどうぞ。
1.マンデルブロ集合とは何か?
マンデルブロ集合の関数は以下です。
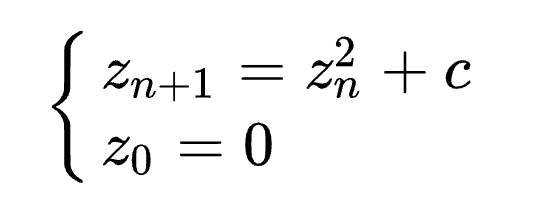
ここで、 ‘c’ は 複素数です。
複素数列であり、かいつまんで言うと、上述の”繰り返し”の中で、どんどん値が大きくなっていくが、無限大に発散しないものです。
参考:フィボナッチ数列
「データ視覚化/ダッシュボードデザインを成功させる95のチェックリスト」をダウンロードする
2.マンデルブロ集合の使い道
マンデルブロ集合はそれ自体美しいものではありますが、実務的な適用はとても限られています。しかしながら、以下のような場面で使われています。
2-1.暗号化
最近の調査では、銀行やコミュニケーションの暗号化のためにもその可能性が検討され、活用されているようです。
Kumar, Suthikshn. “Public key cryptographic system using Mandelbrot sets.” MILCOM 2006-2006 IEEE Military Communications conference. IEEE, 2006
2-2.コンピュータのパフォーマンスにおけるベンチマーキング
ベンチーマーキングでの活用です。こちらが最もよく知られている例でしょう。マンデルブロ集合のシンプルなプログラムが複雑な多くのパターンを生成するため、プログラミング言語のパフォーマンス、効率性を測るのに有用です。
2-3. 生物学
生物学の場面では、マンデルブロ集合のフラクタル幾何の複雑性から神経樹状突起のパターンを予測・分析することに使われており、どのように細菌が成長するかの示唆にもなっています。
参考:『What are the Fractals?When Do You Use Them In The Real World?』
3.参考情報
- Kumar, Suthikshn. “Public key cryptographic system using Mandelbrot sets.” MILCOM 2006-2006 IEEE Military Communications conference. IEEE, 2006.
- Computer language Benchmark Game
- What are fractals? When do we use them in Real World?

データの管理・活用でお困りの場合はデータビズラボへお問い合わせください。
データビズラボでは状況やニーズに合わせた様々なサポートをご提供いたします。






コメント